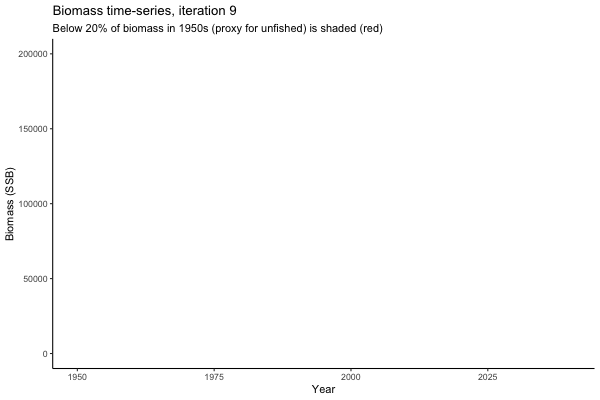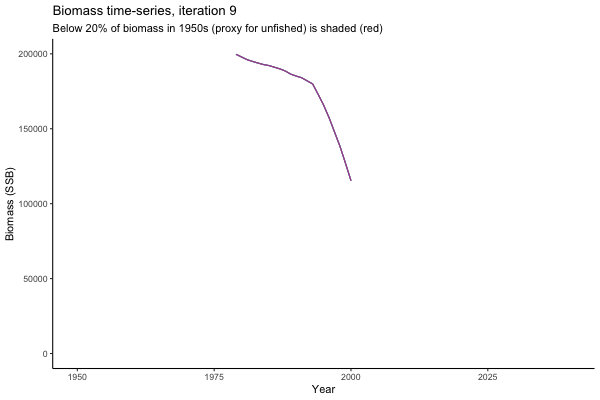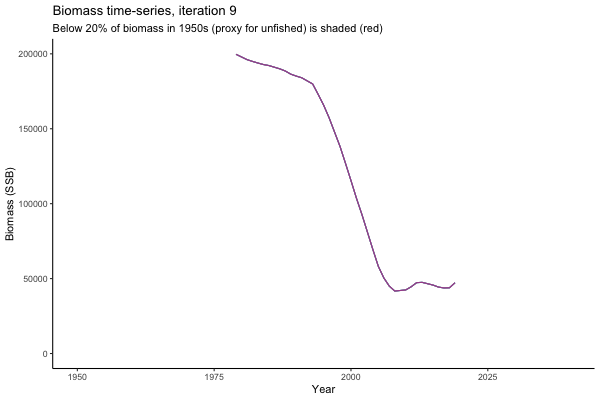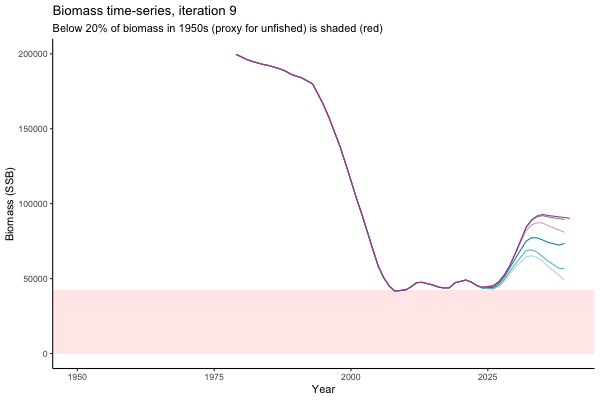
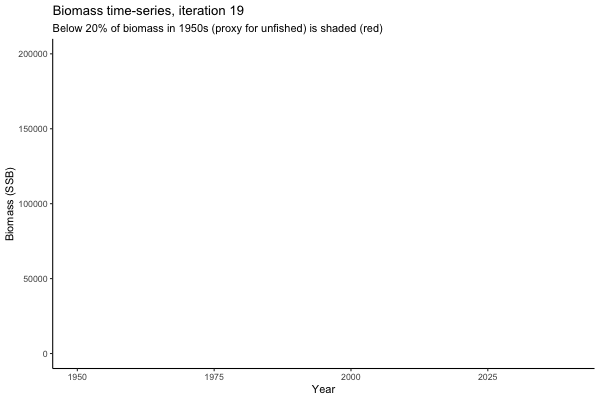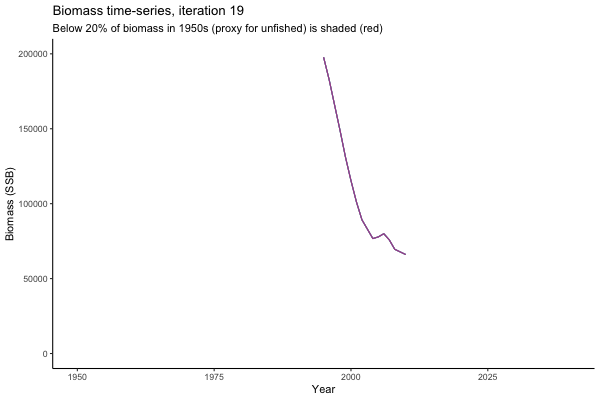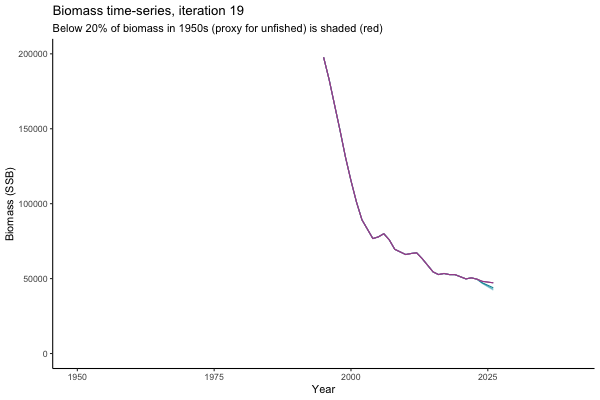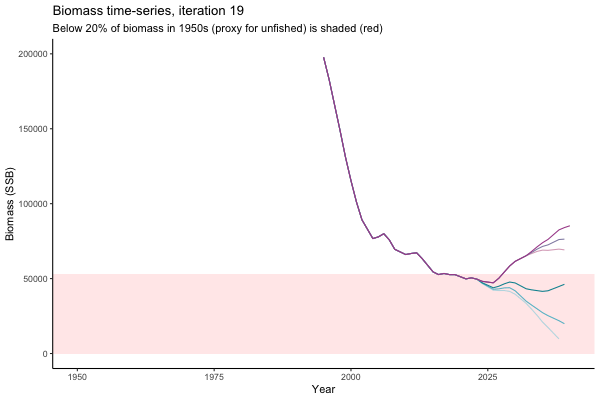
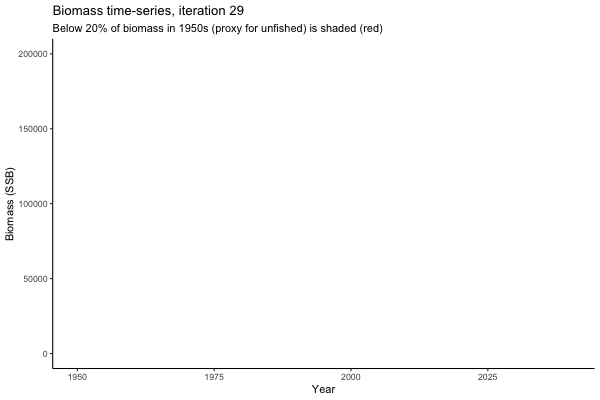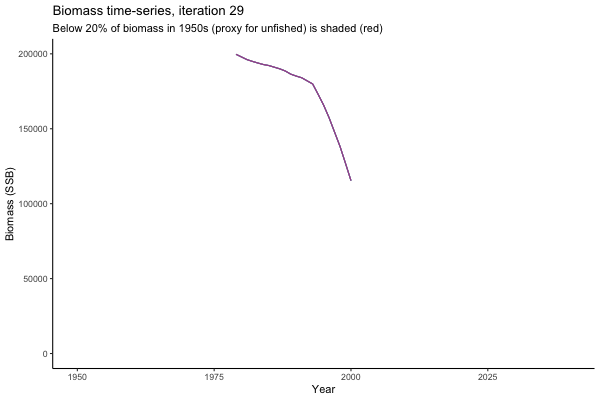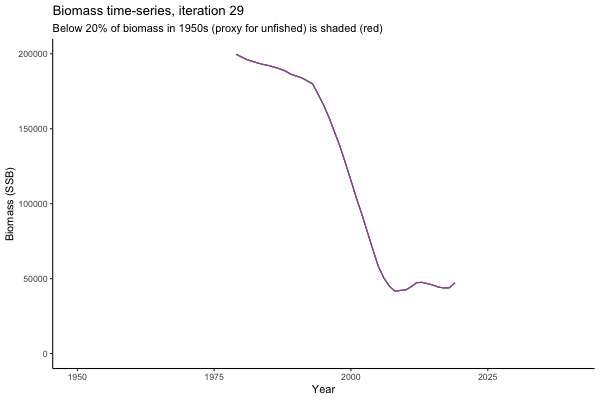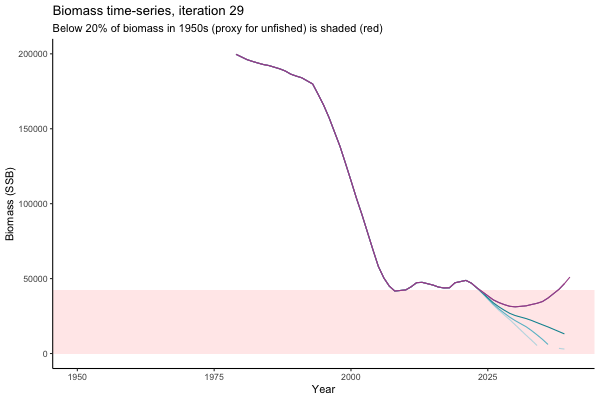
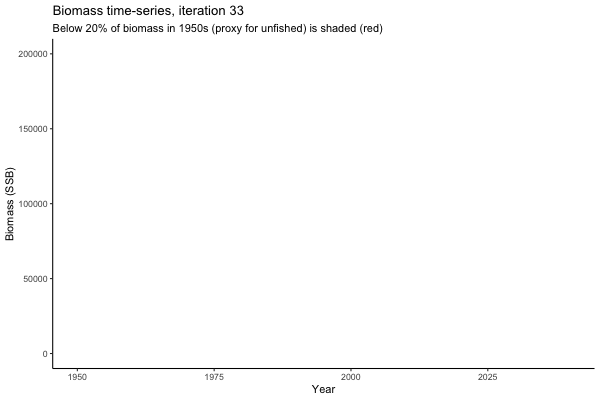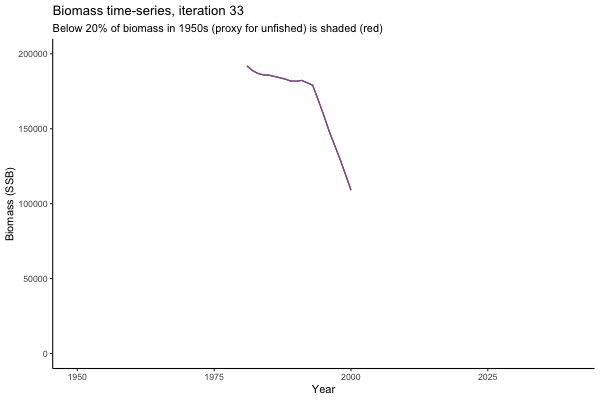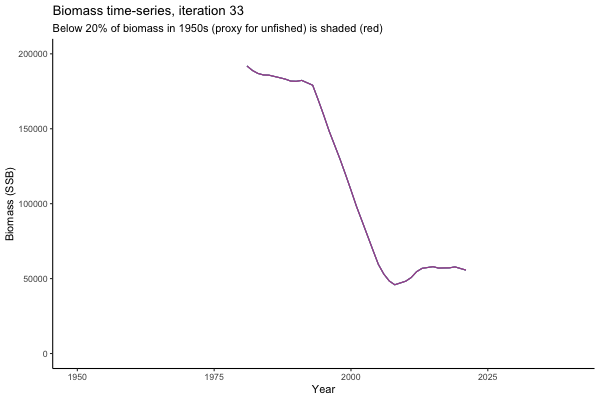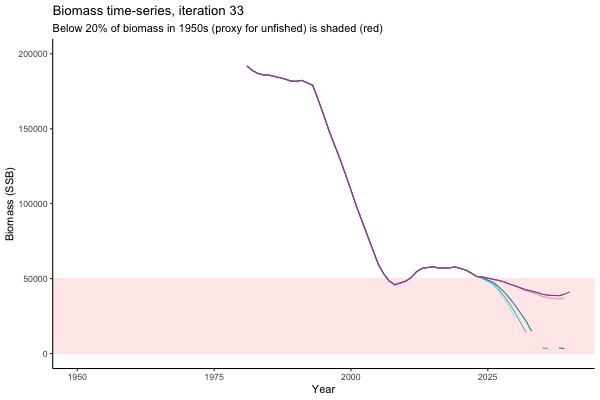
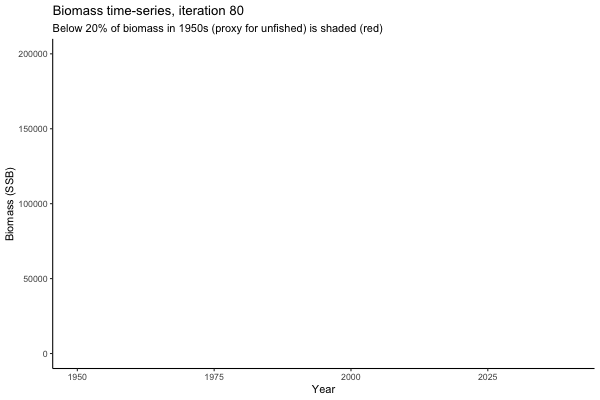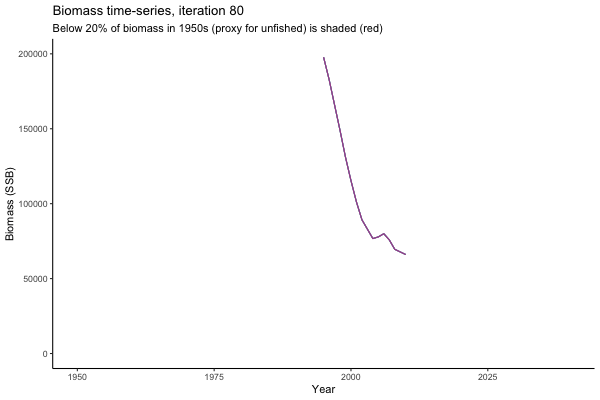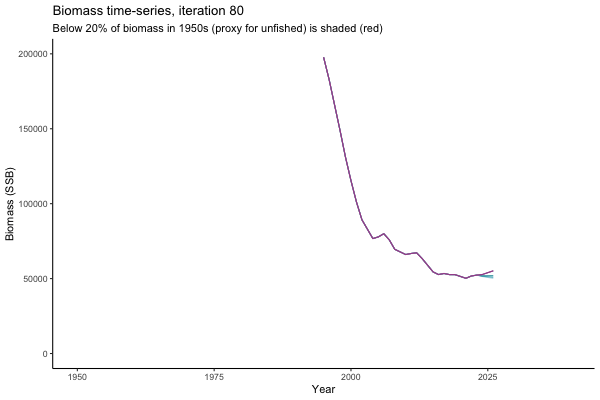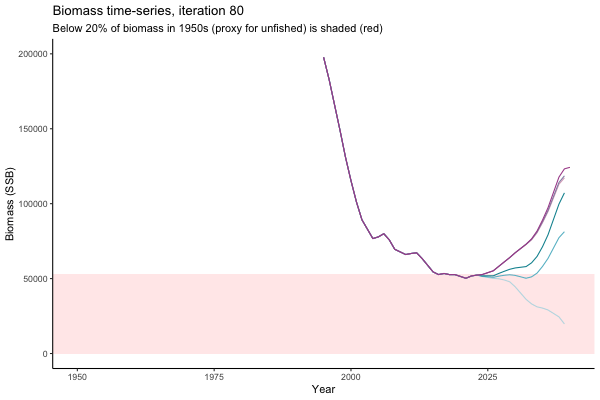
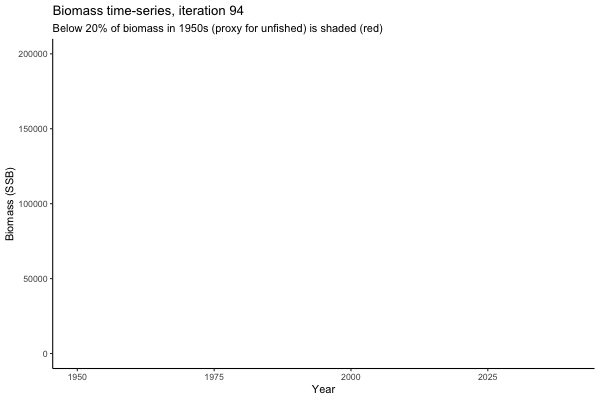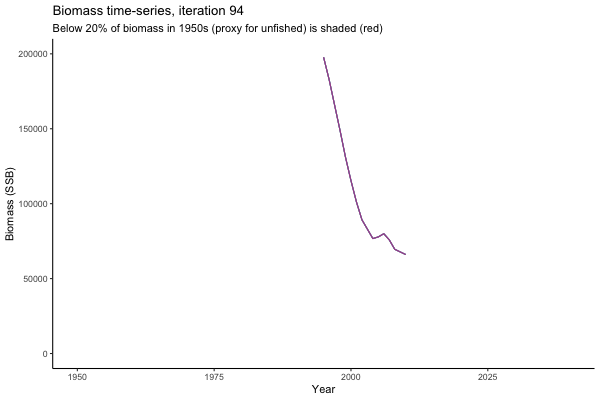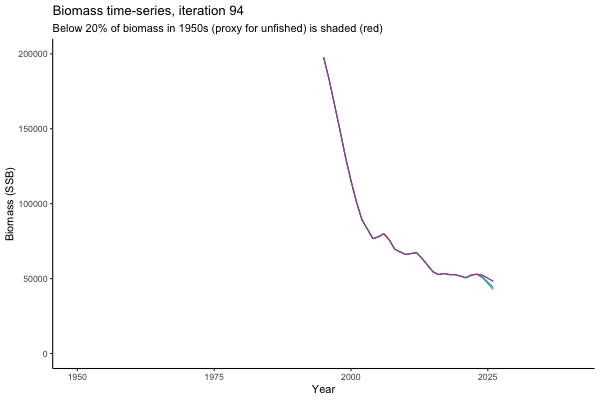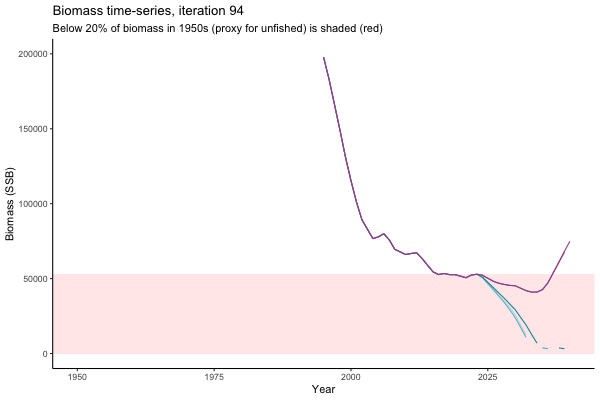
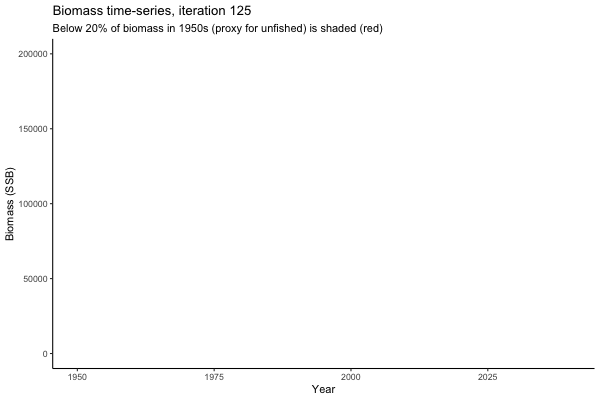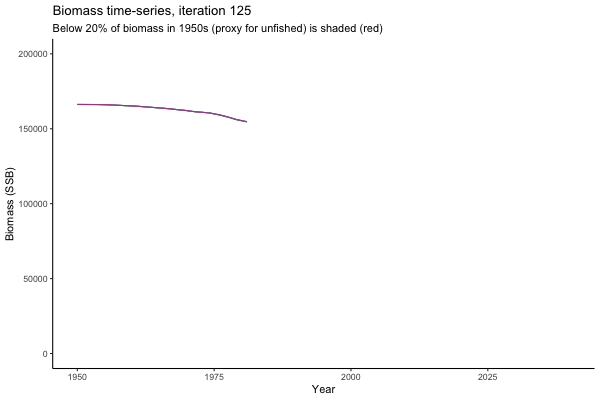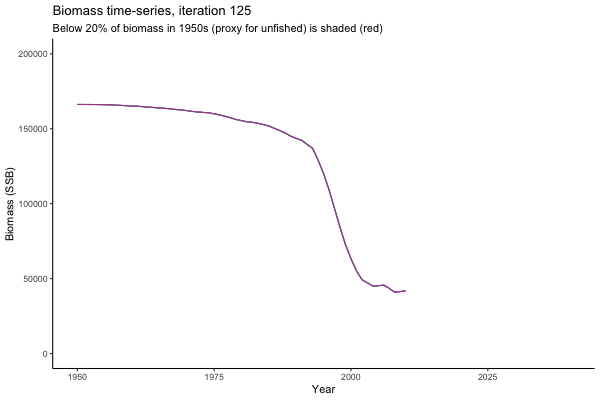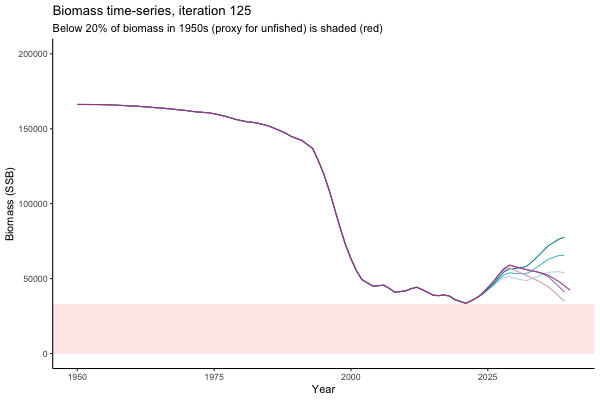
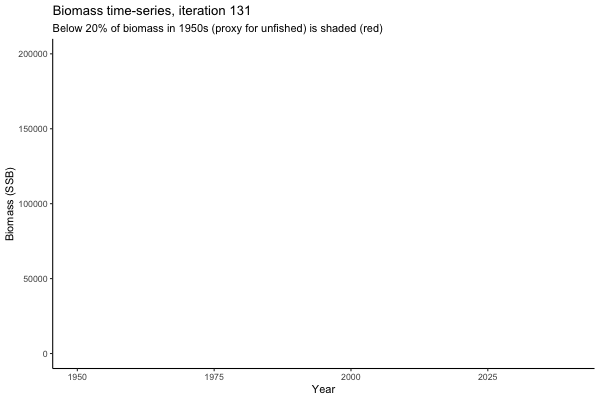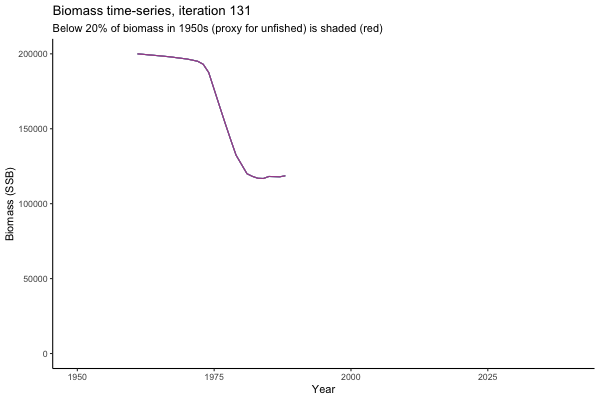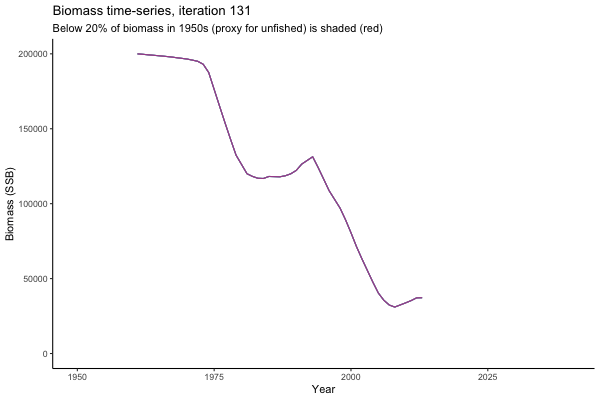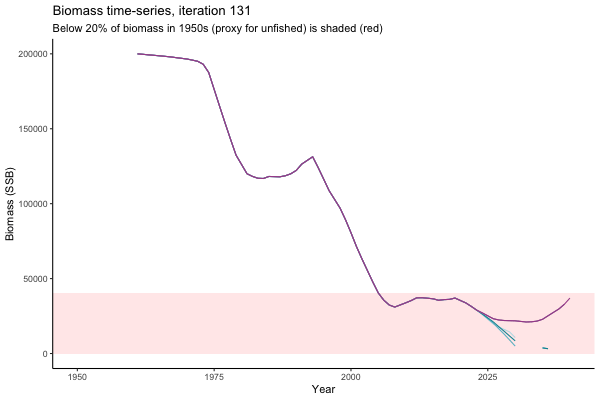
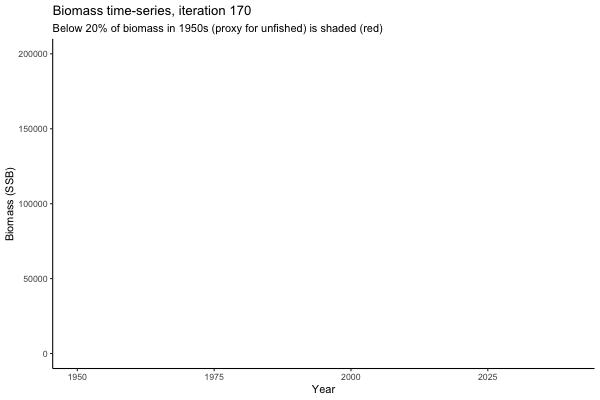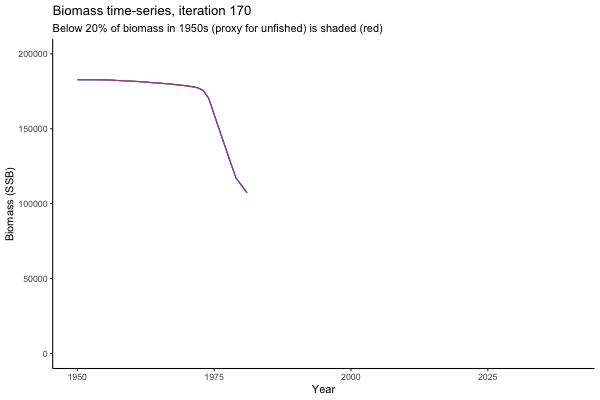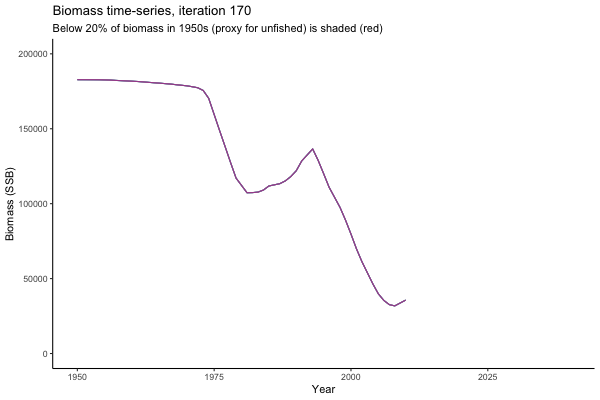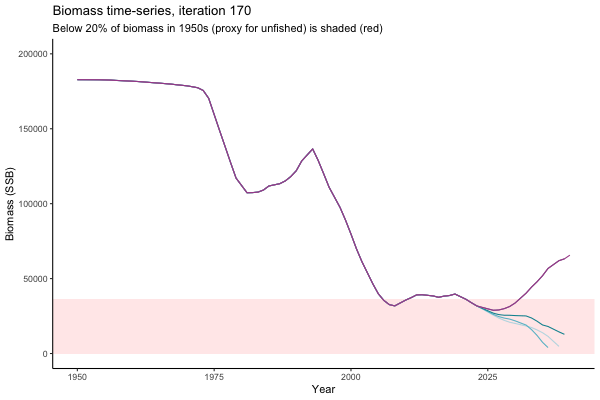
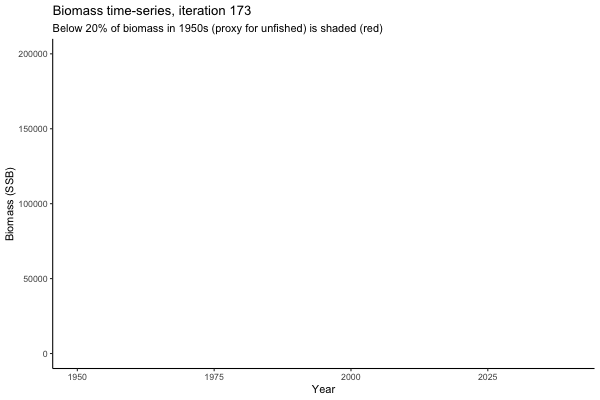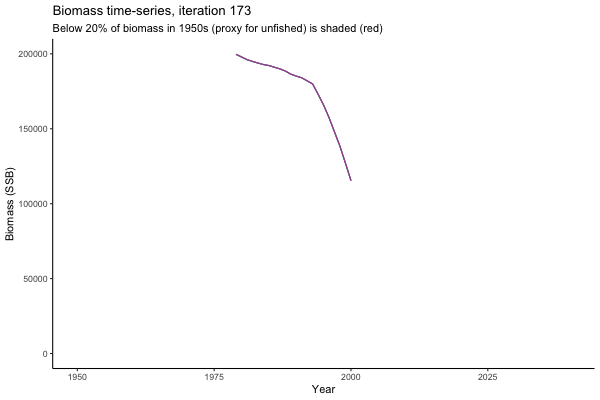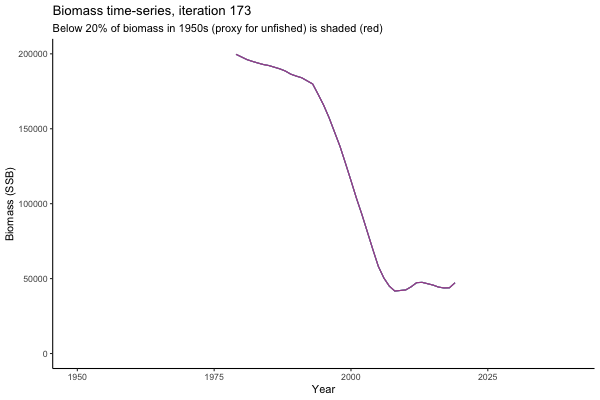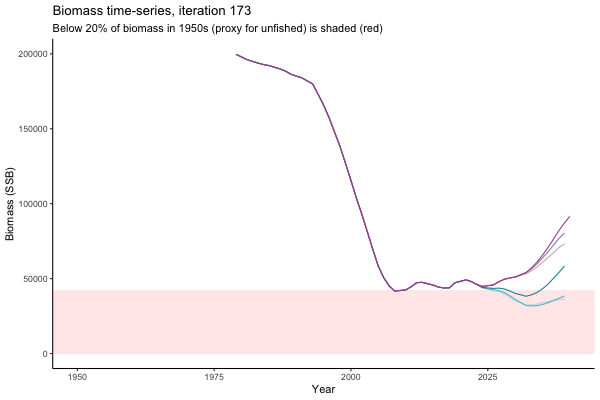
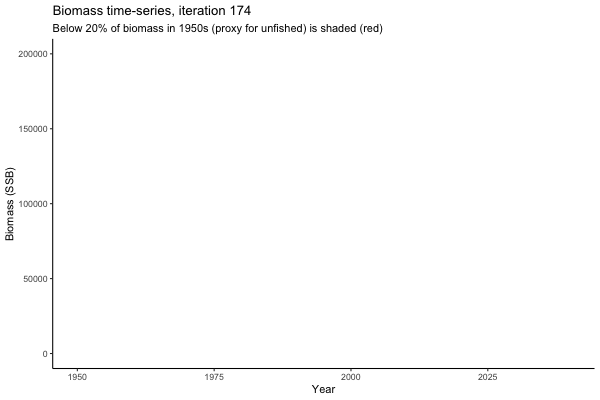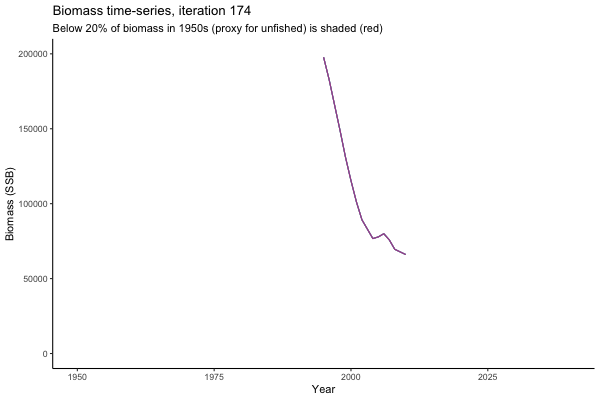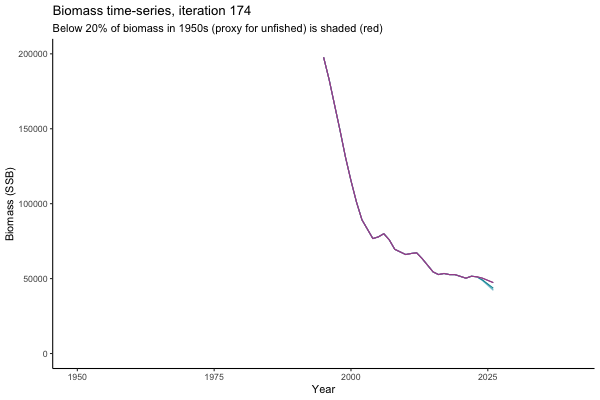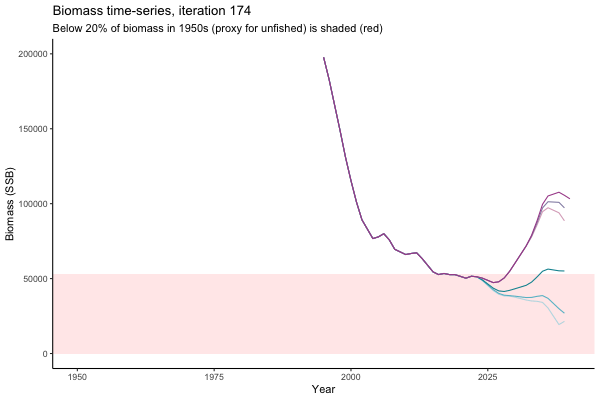
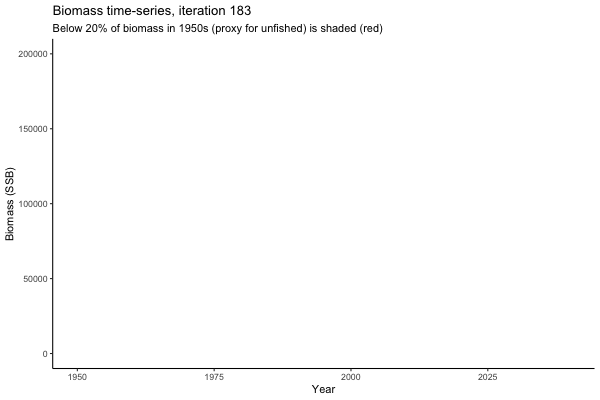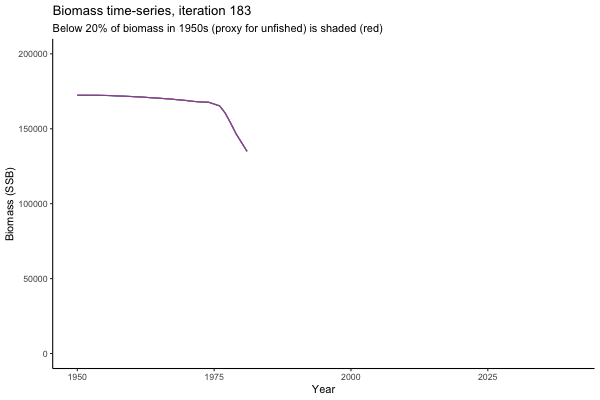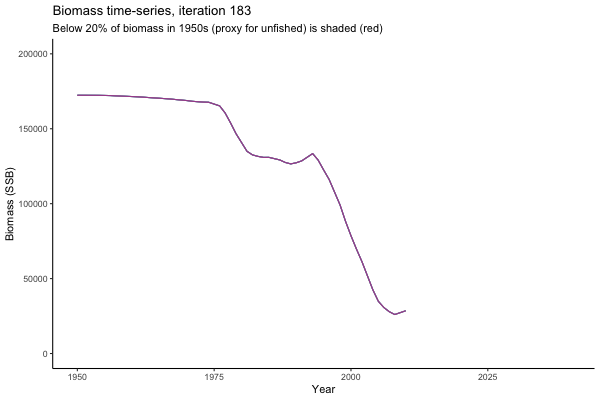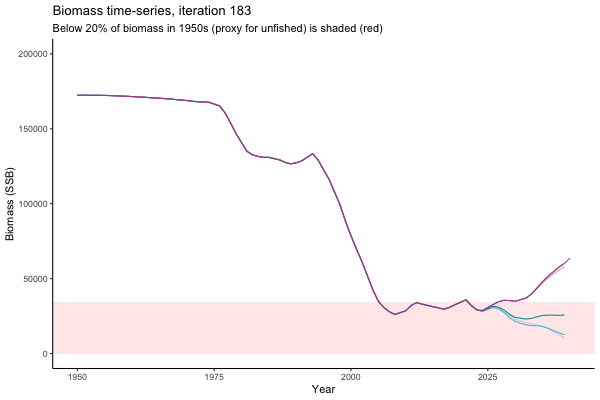
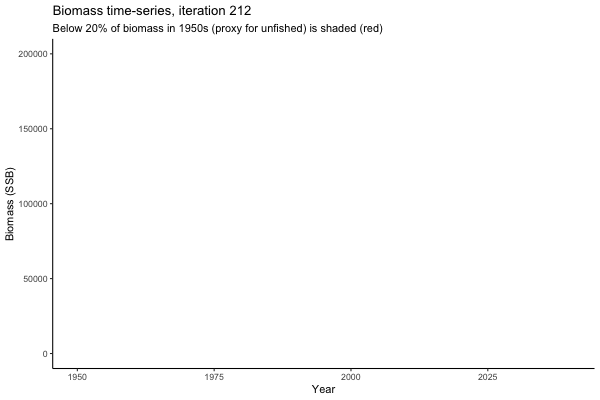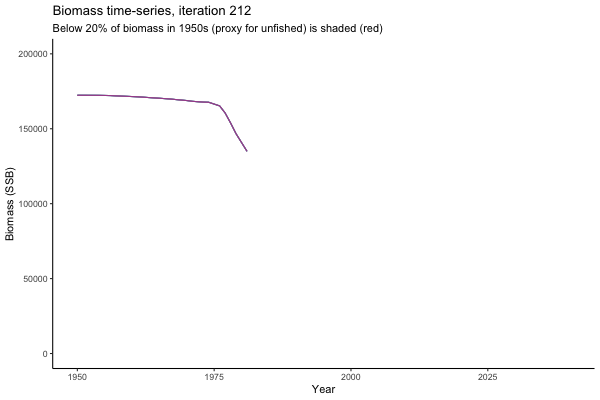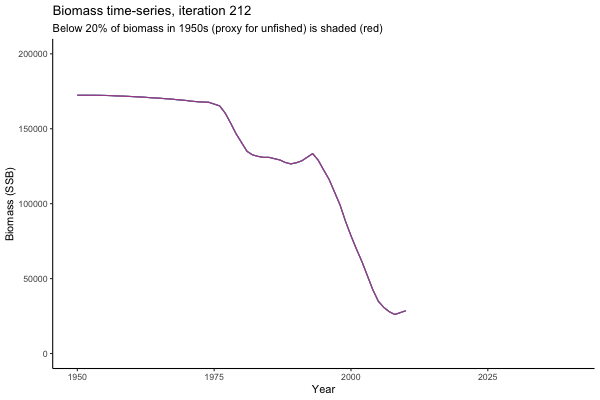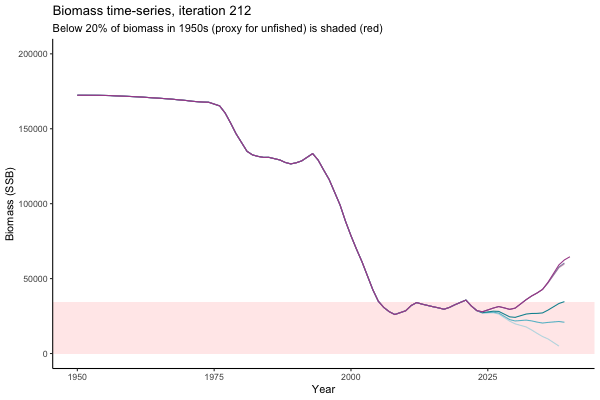
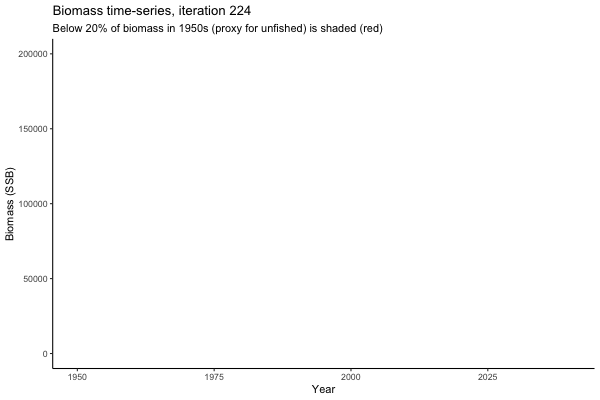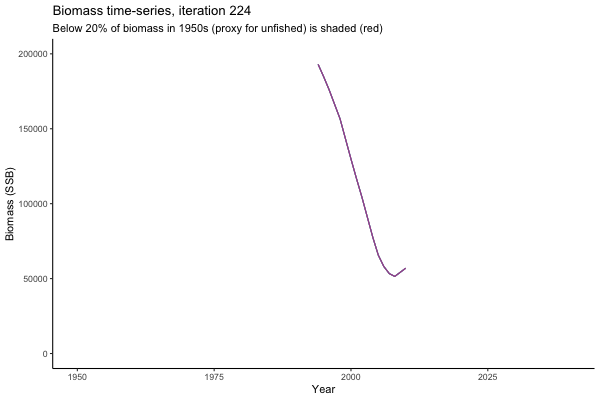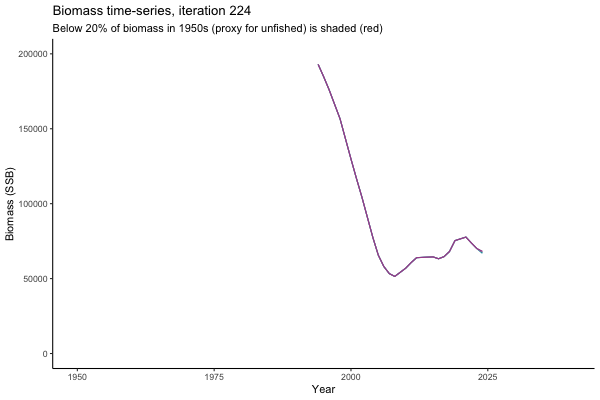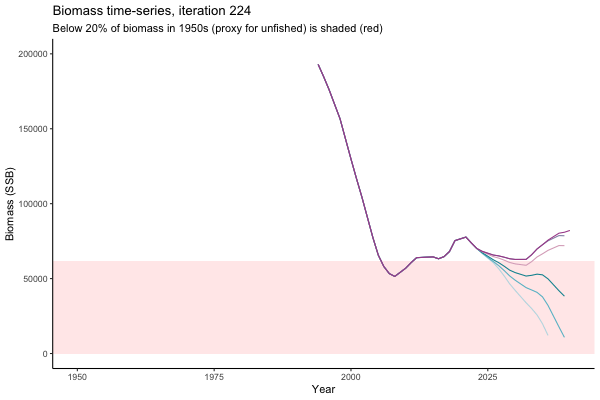
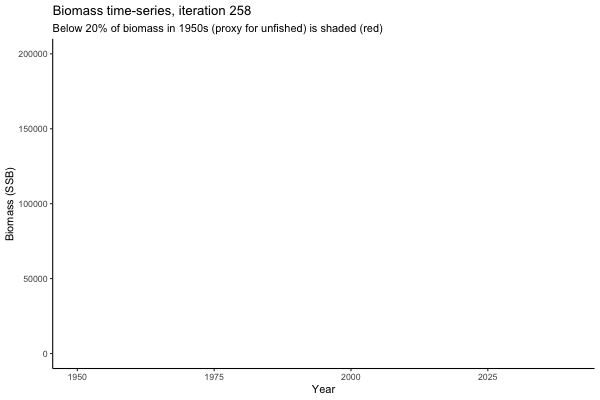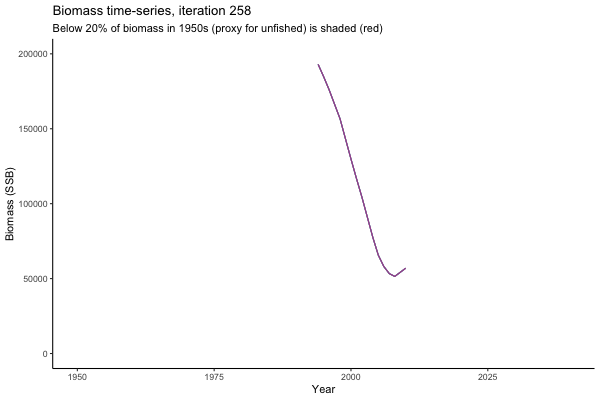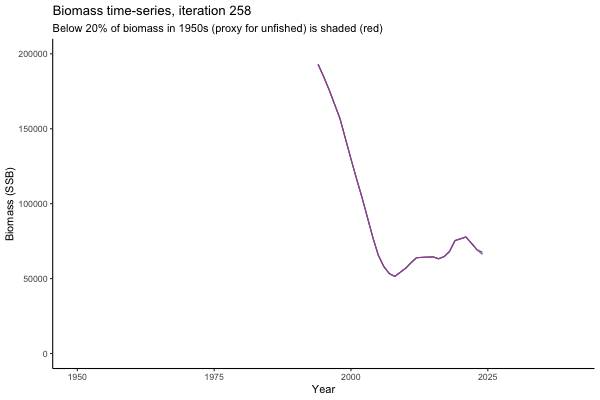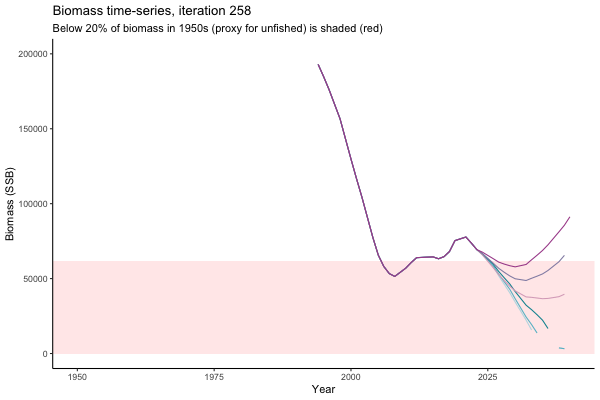
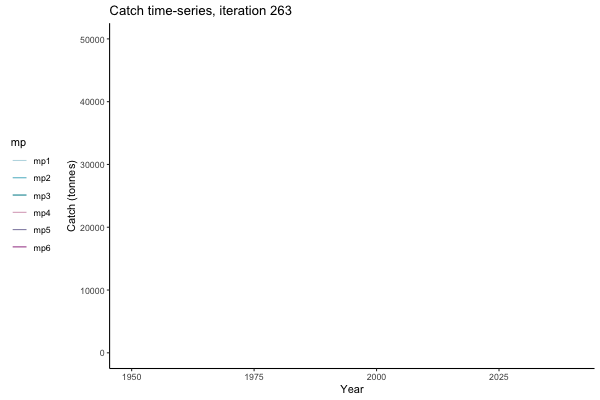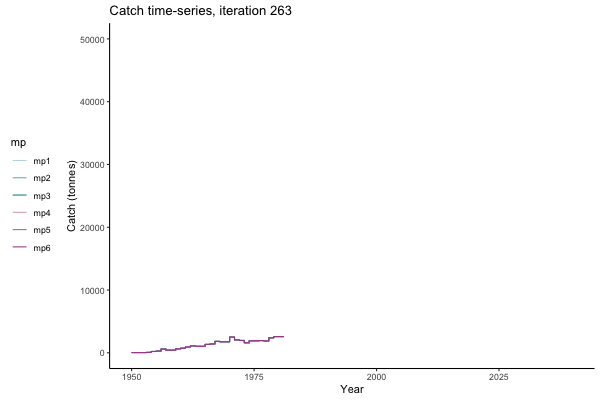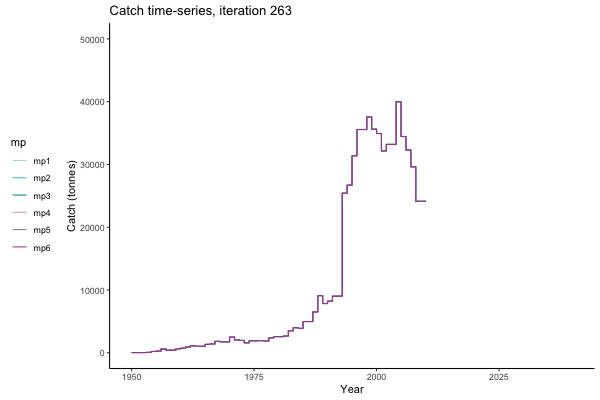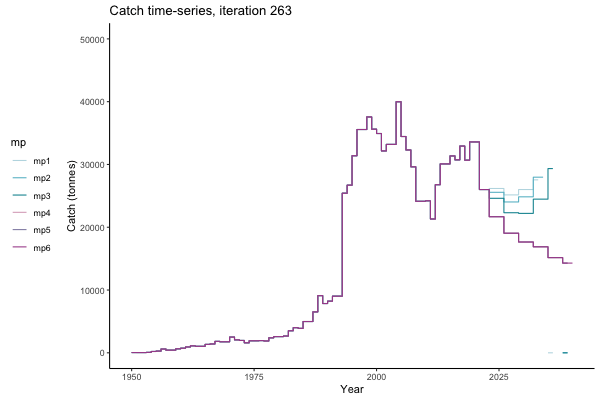
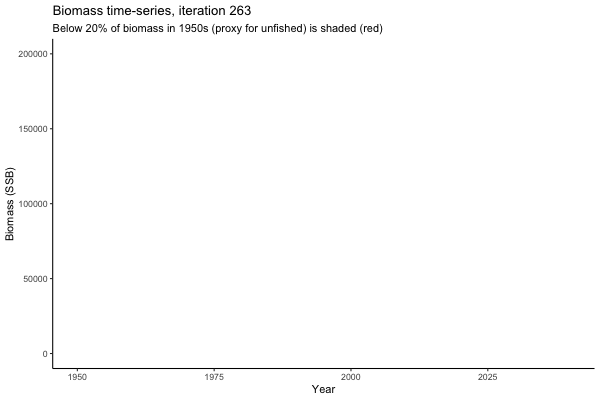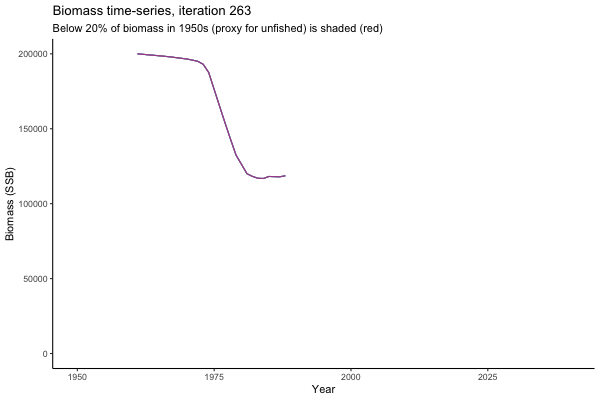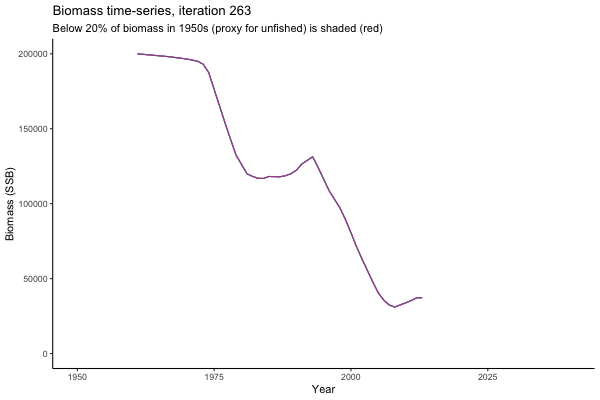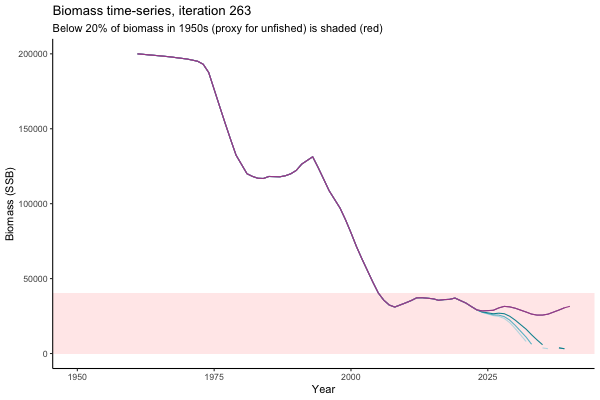
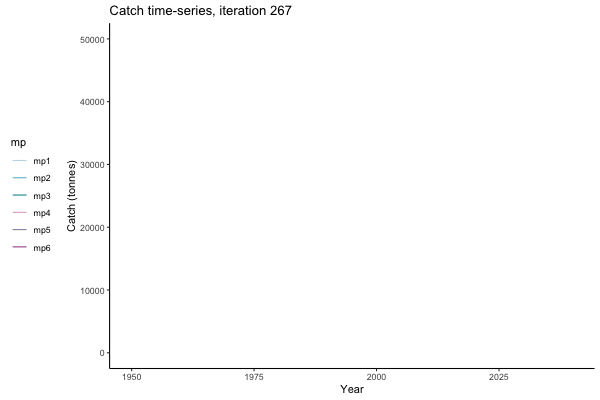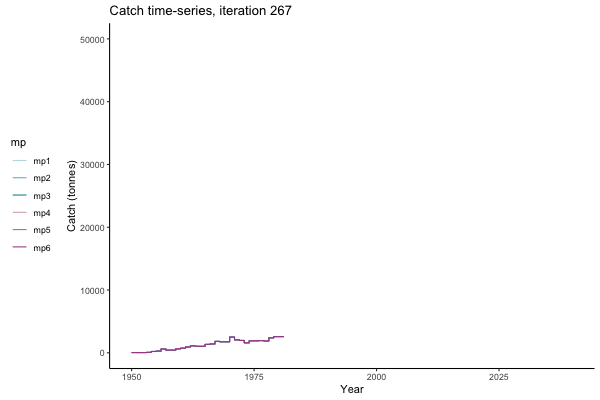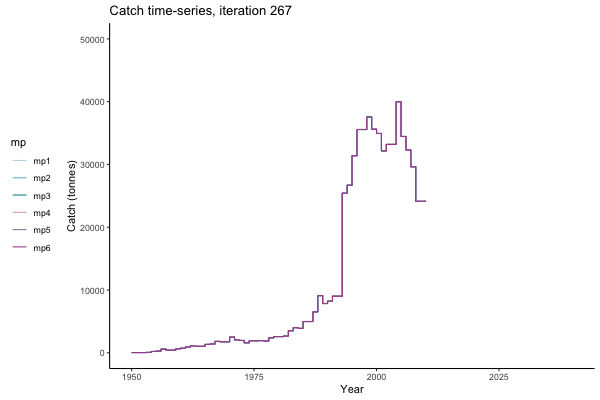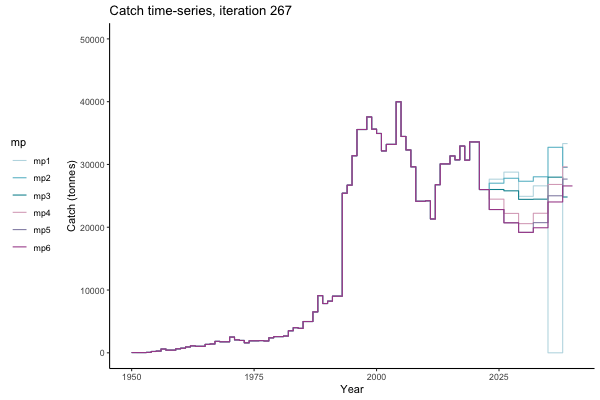
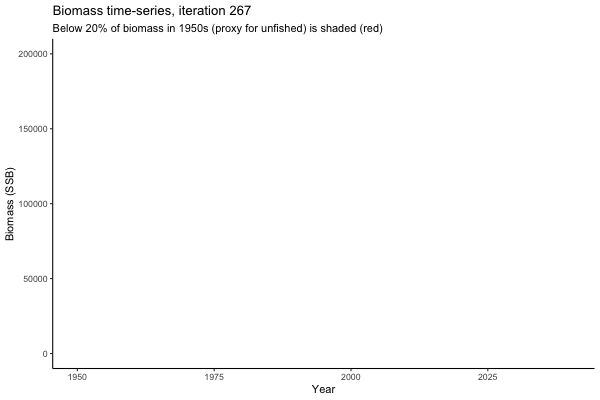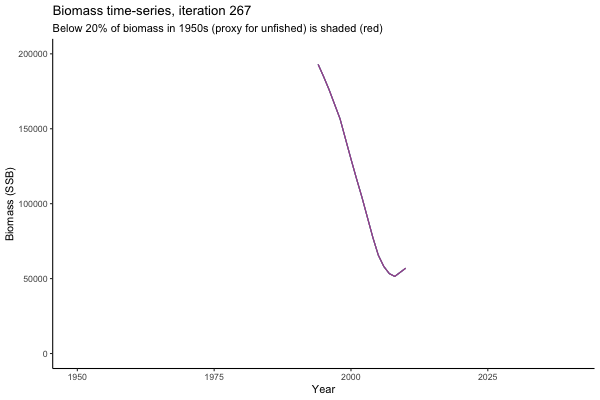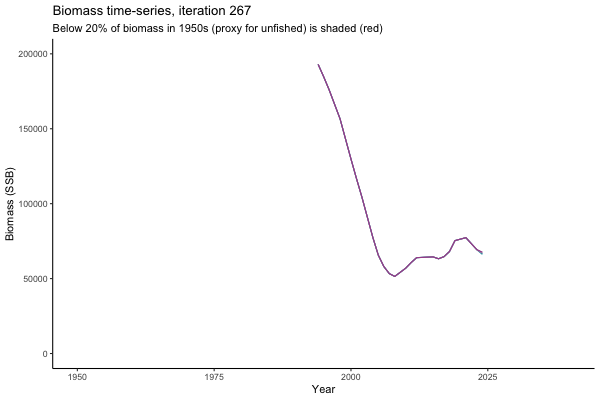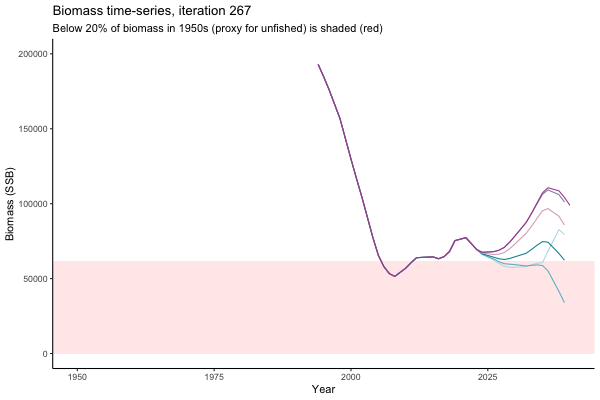
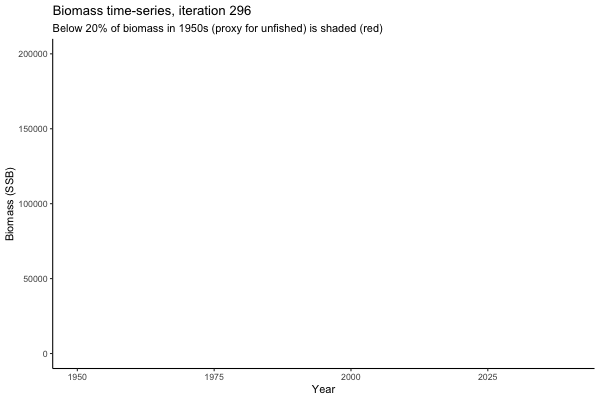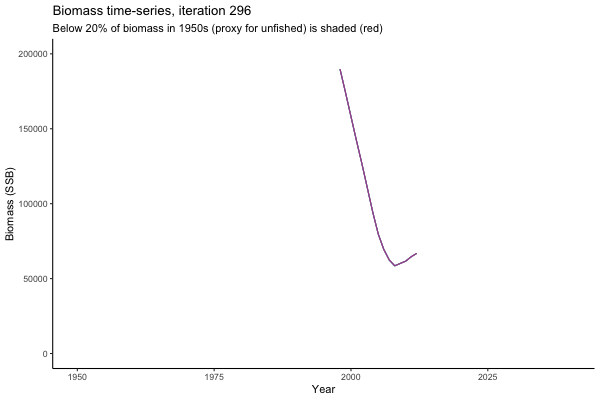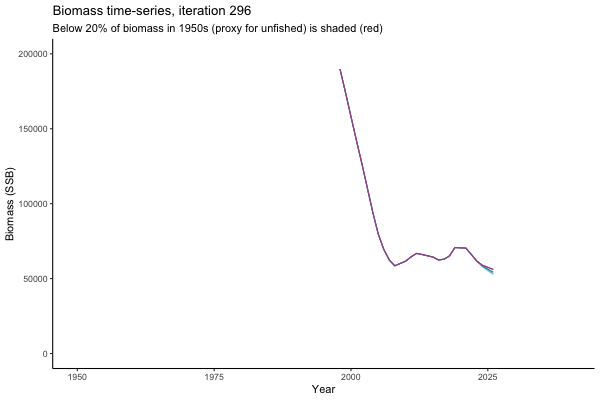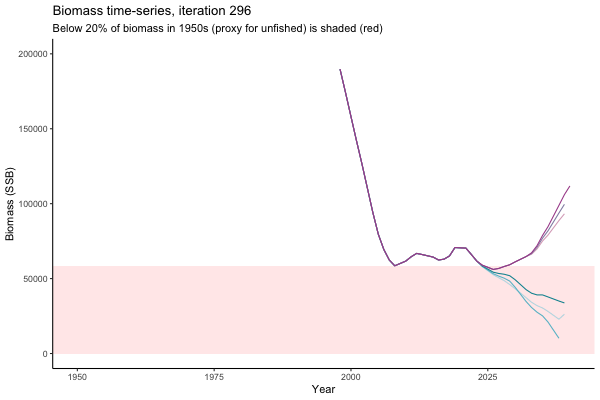
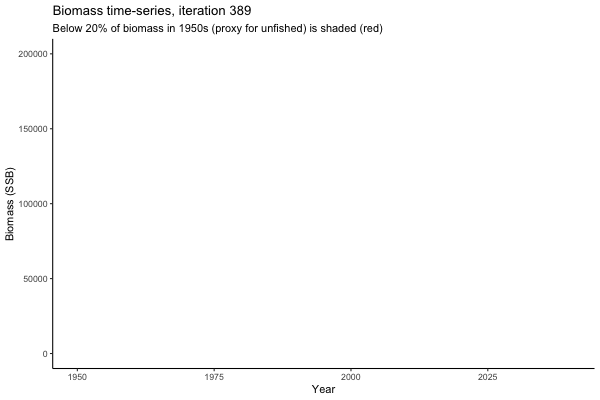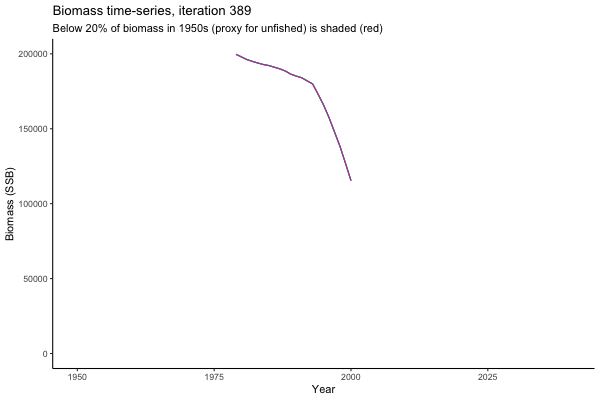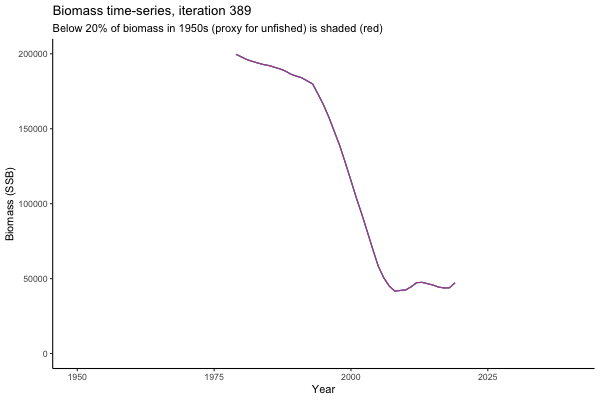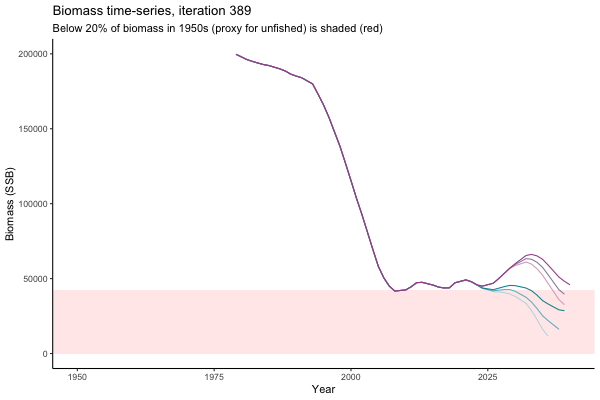
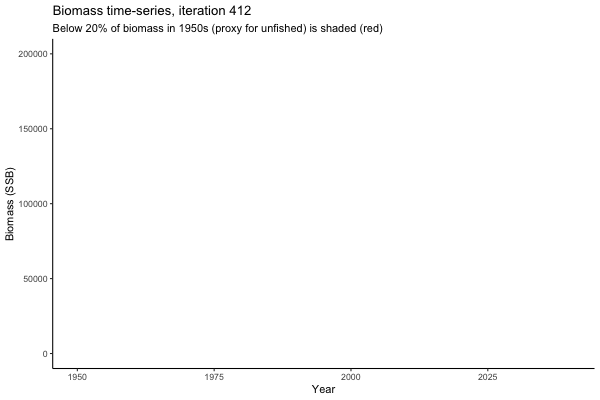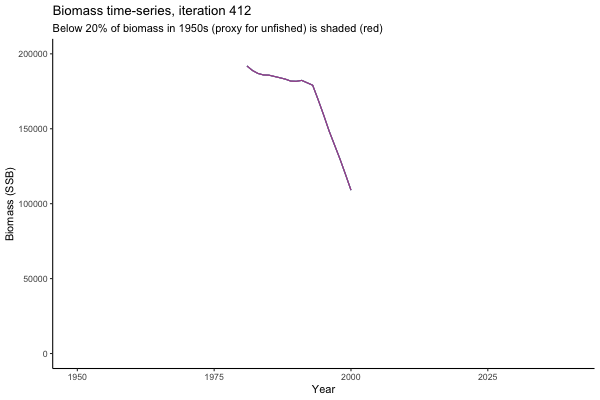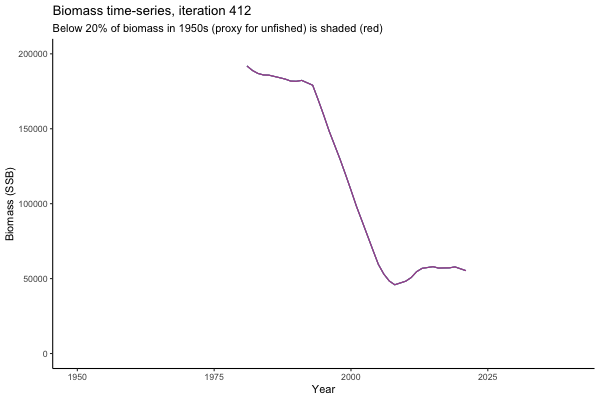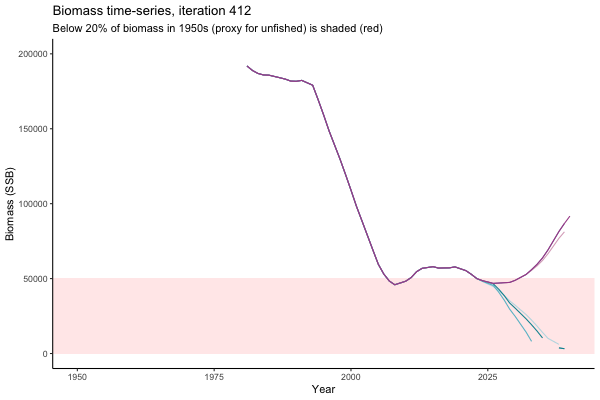
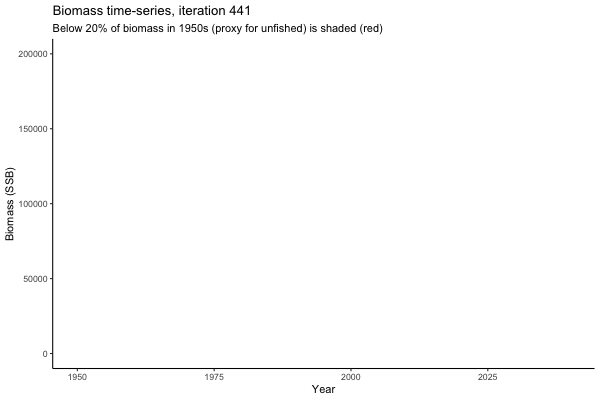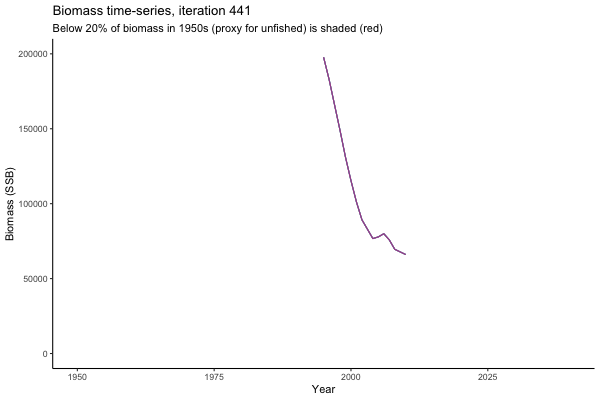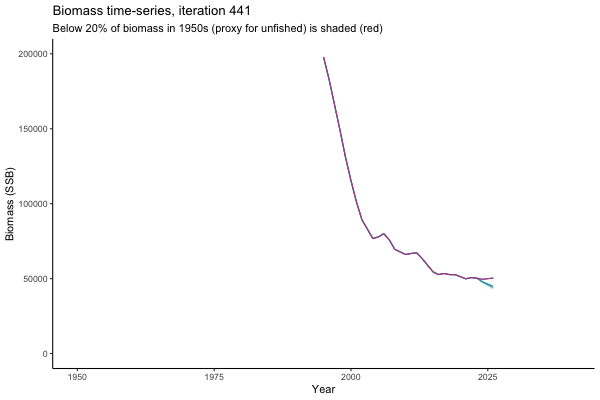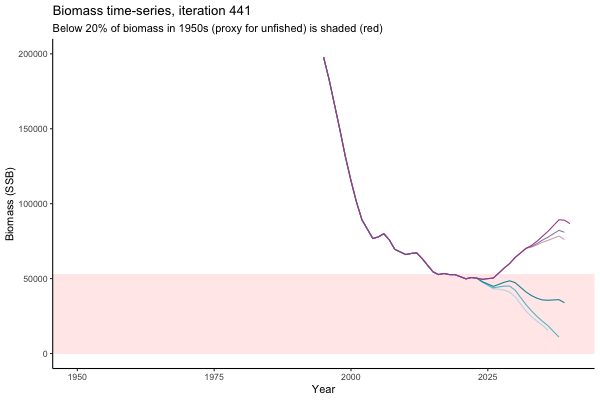
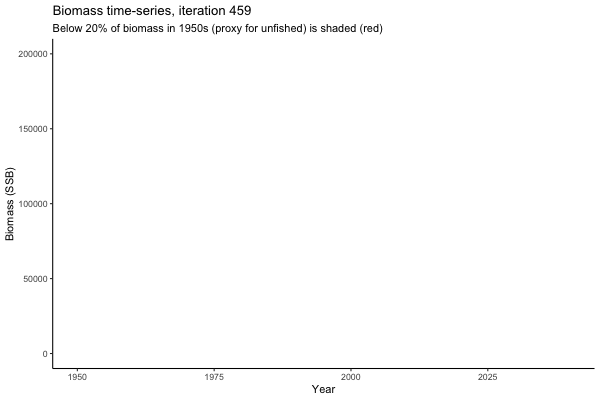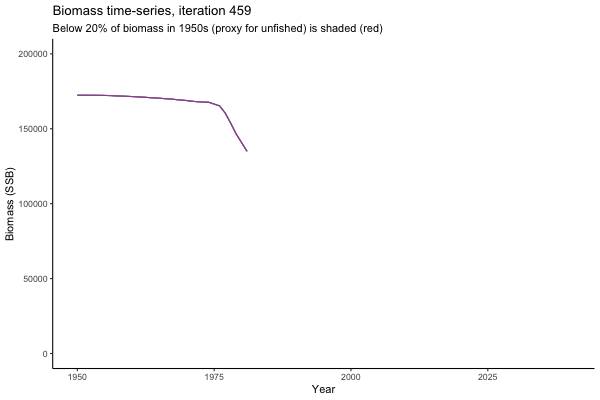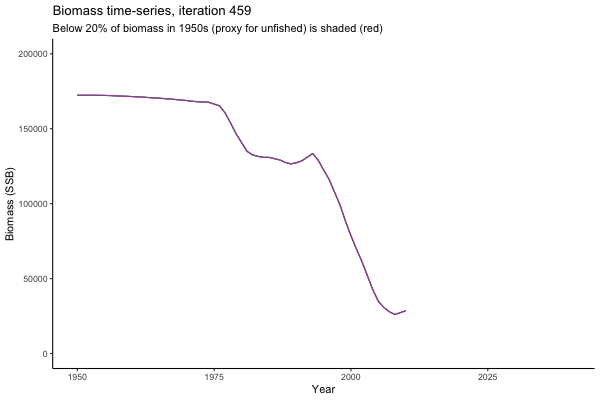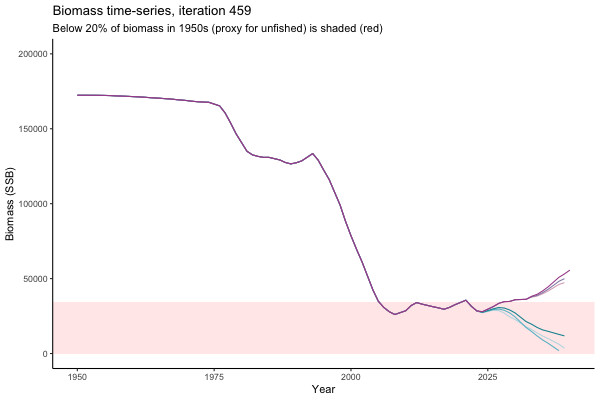
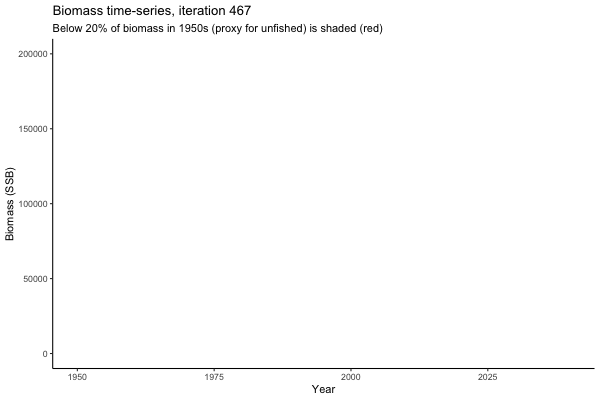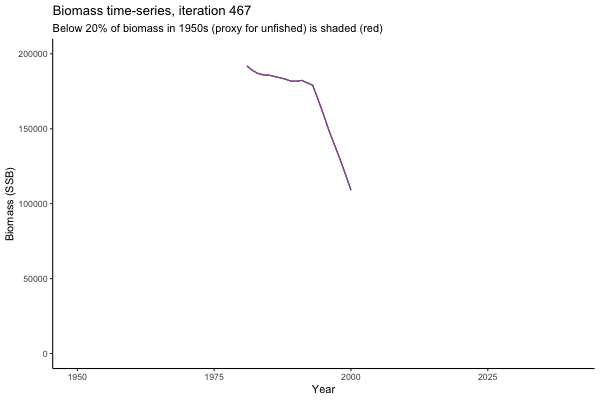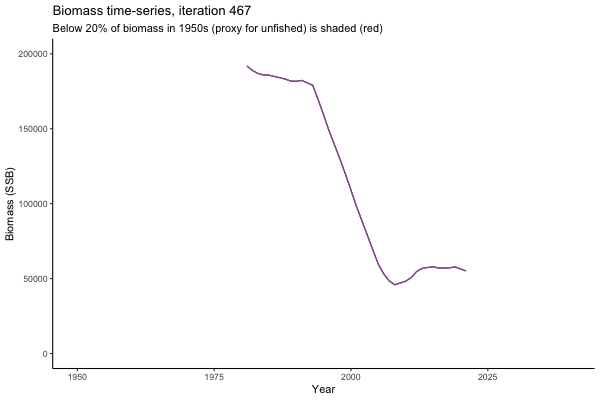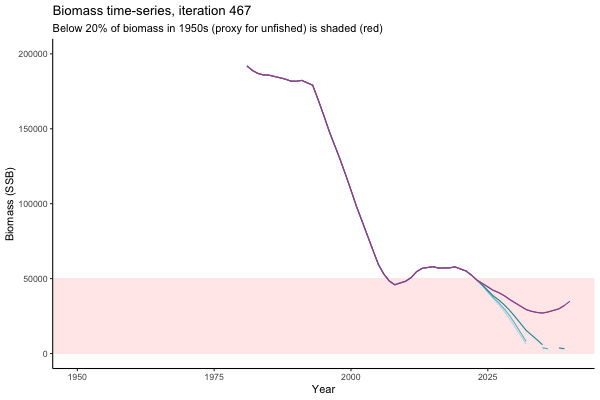
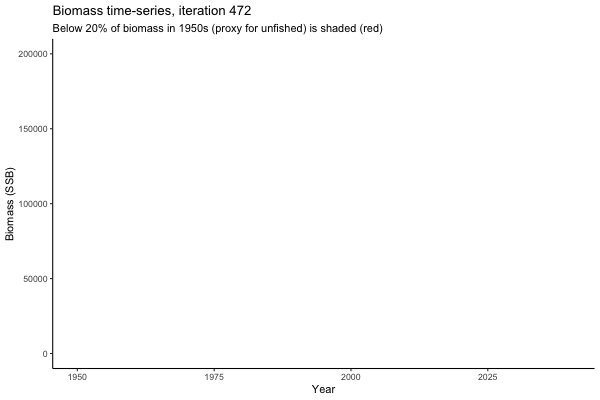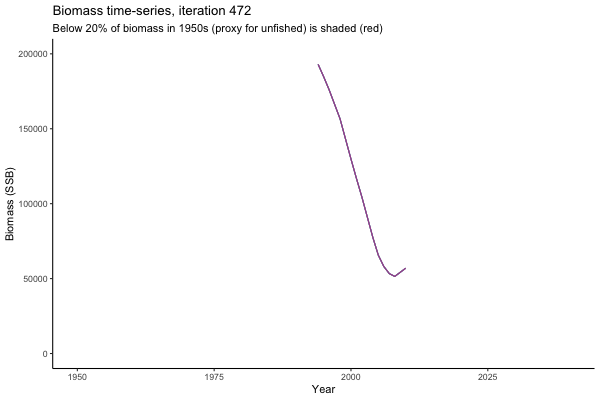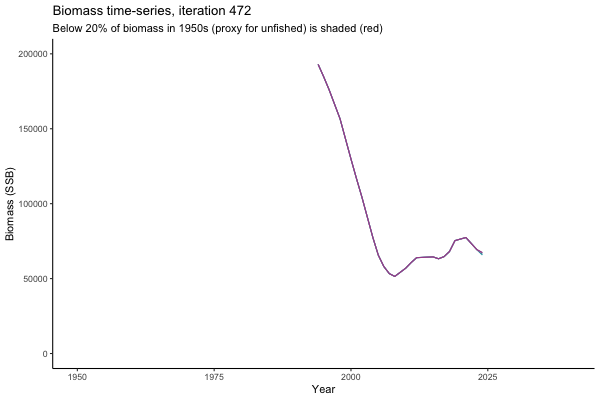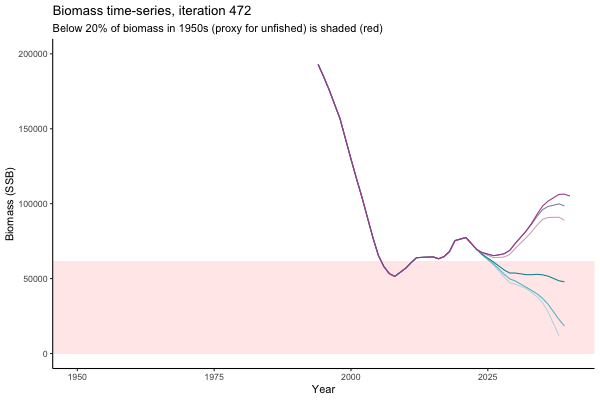
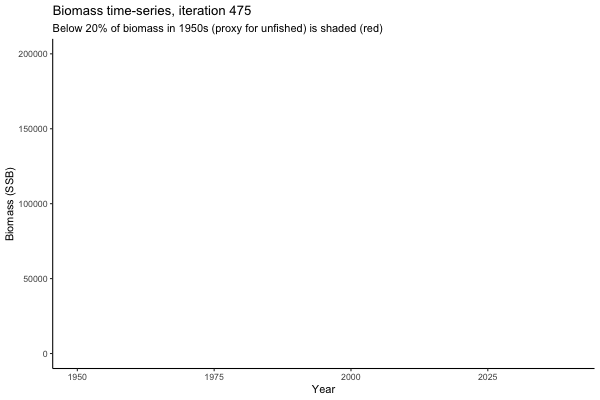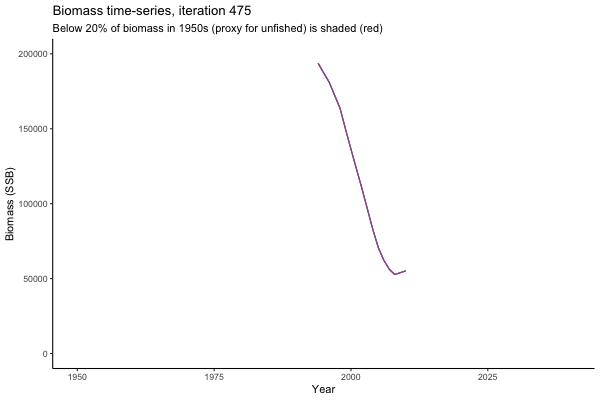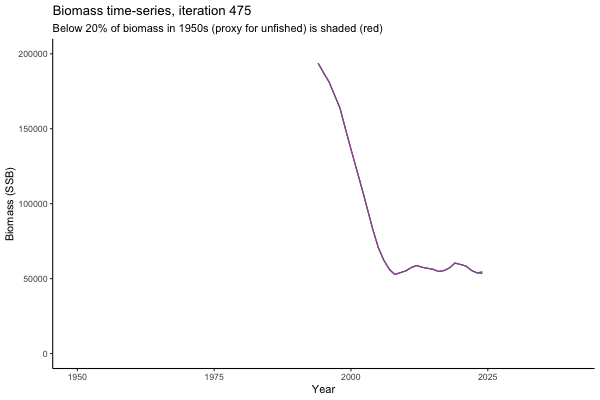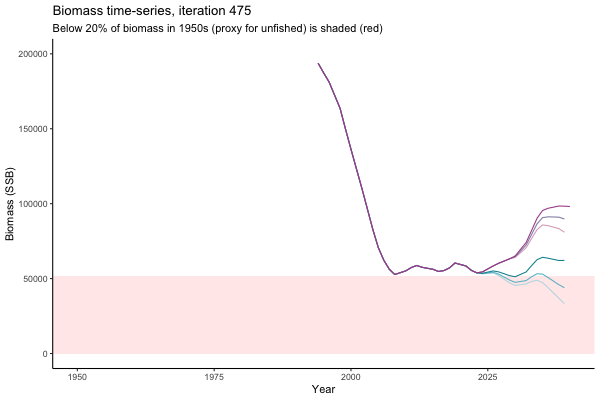
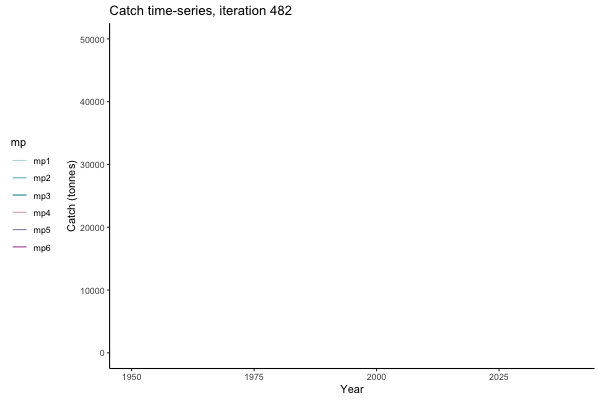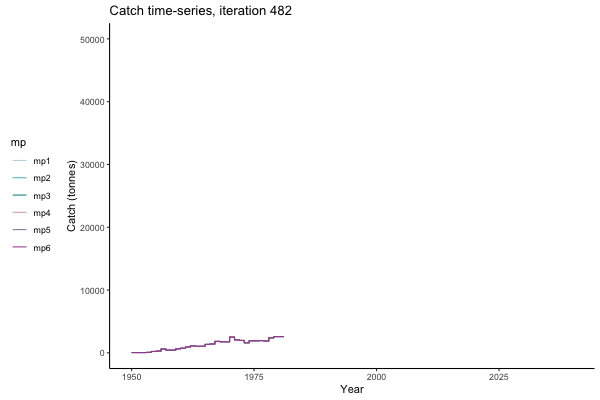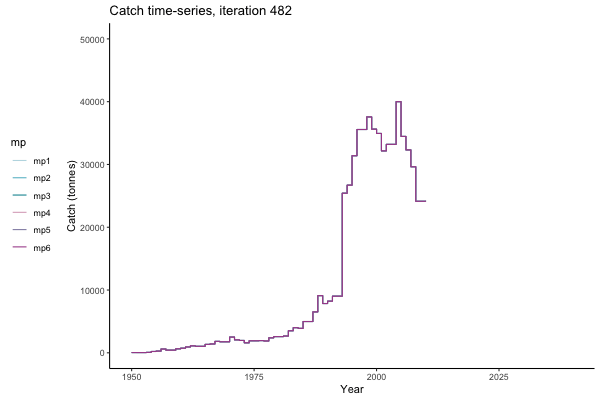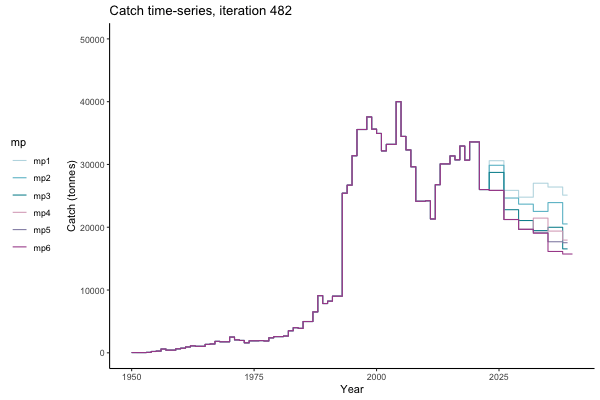
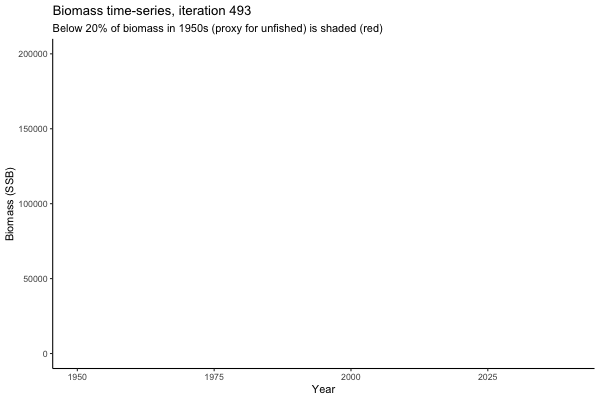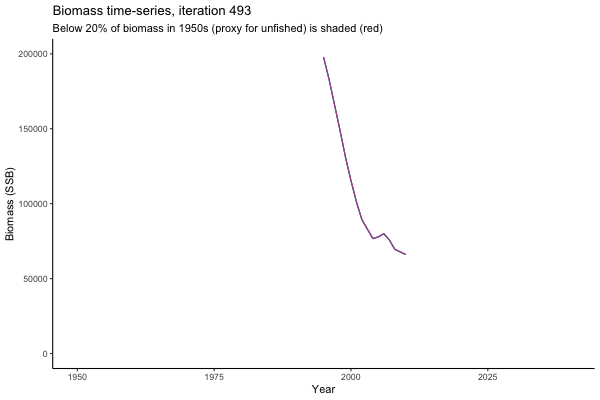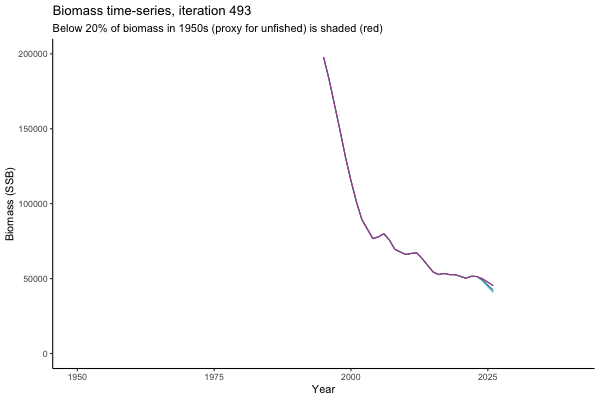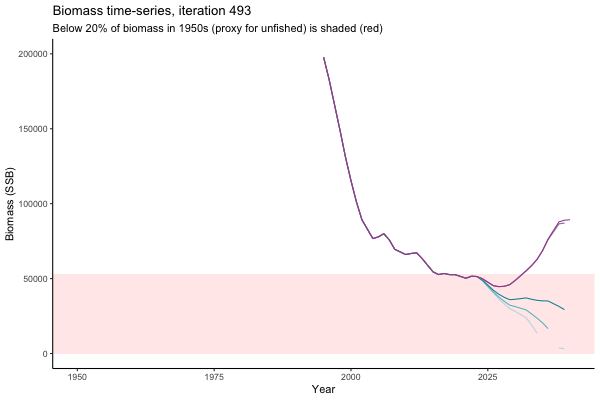
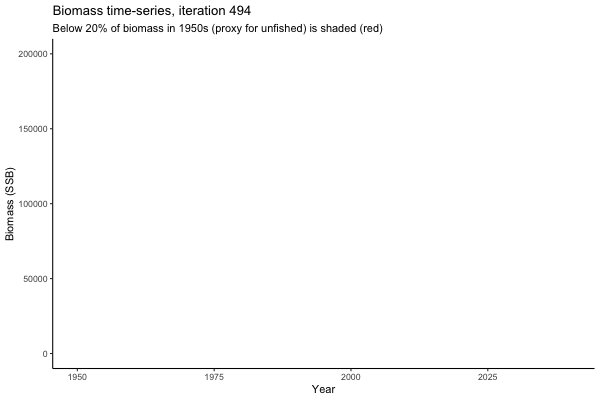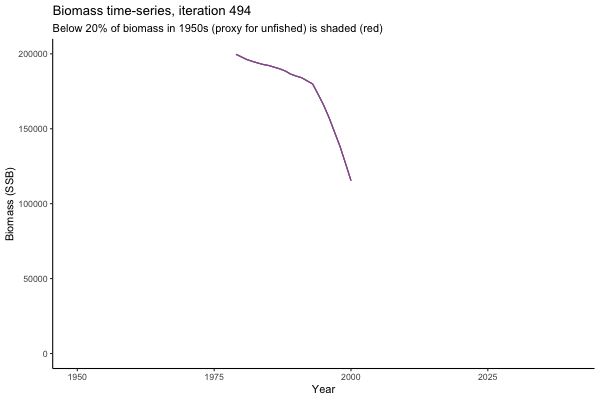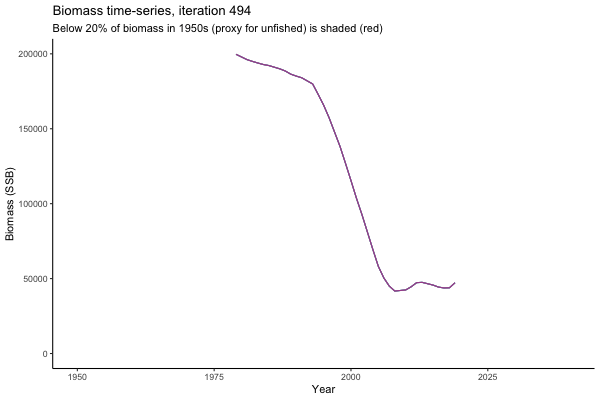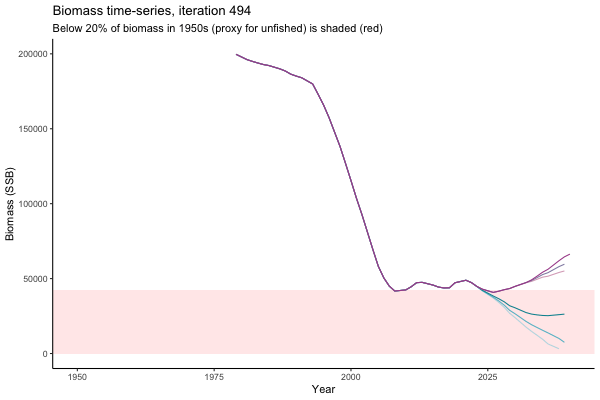
Trajectories
Looking at random individual trajectories is a good way to communicate volatility over time. Here we explore what happens in the same world under different MPs and get a sense of how tuning works.
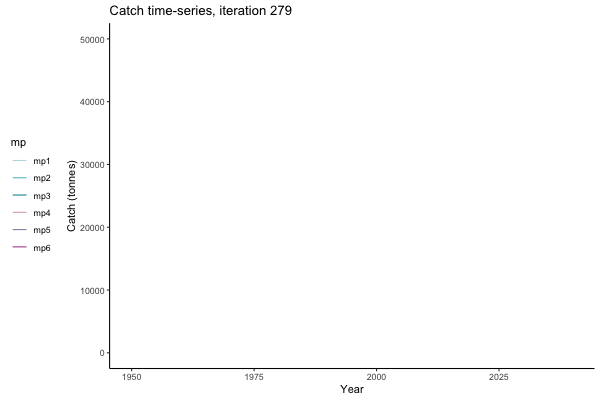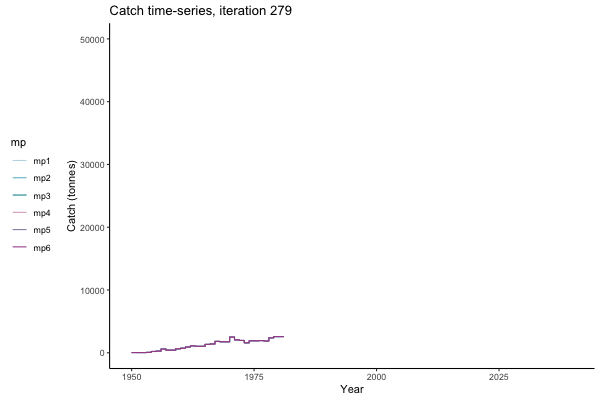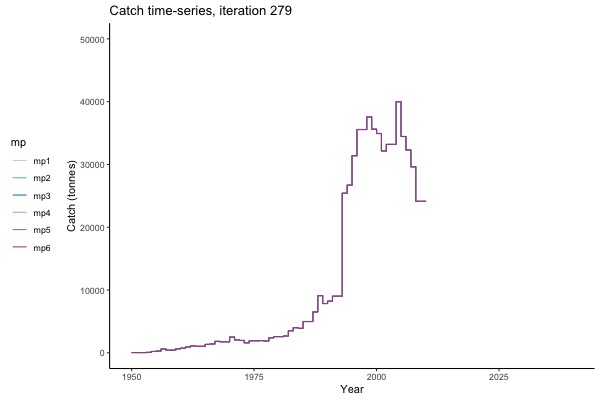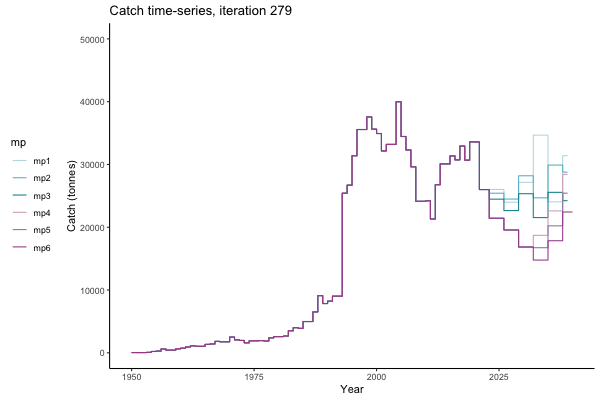
All MPs set TAC for 3 years at a time, no implementation error is modelled (e.g. it is assumed that TAC equals actual catch) and the maximum change allowed is 15% of previous TAC — thus the step function visualisation is more appropriate for catch.
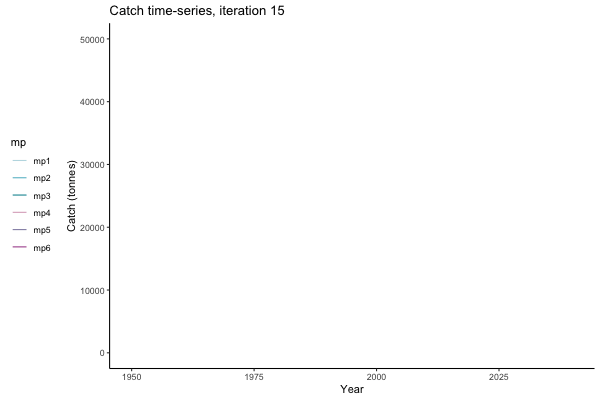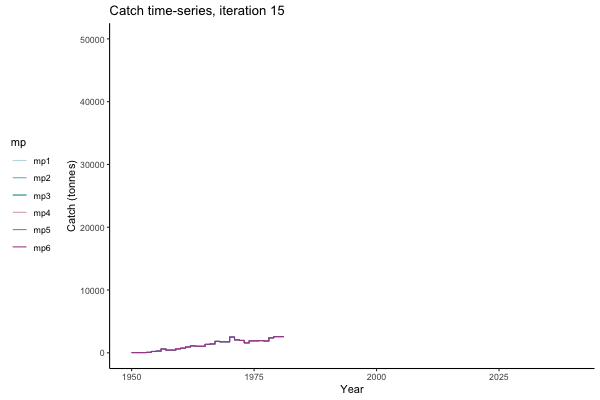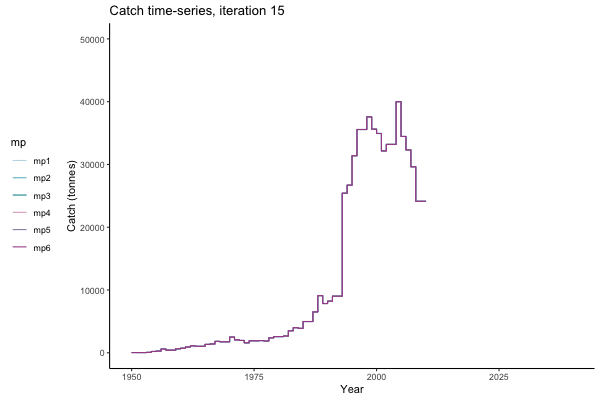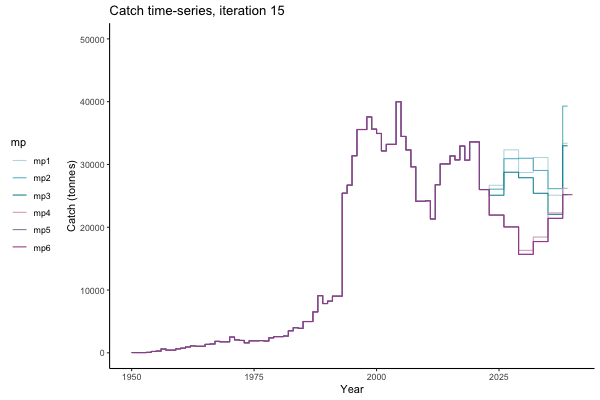
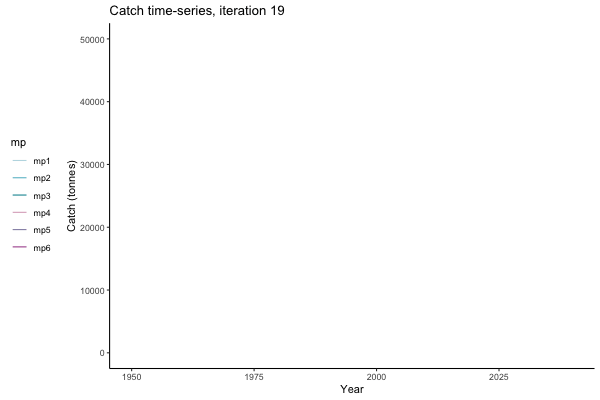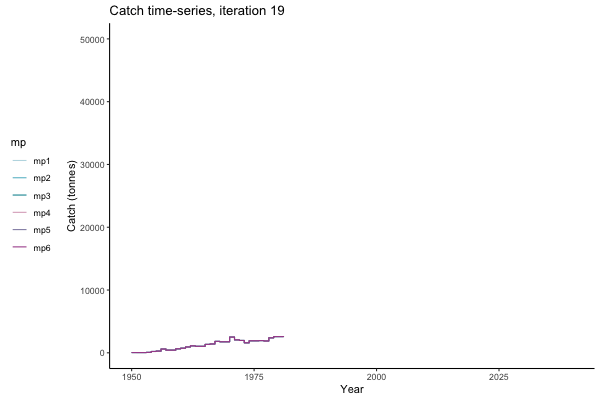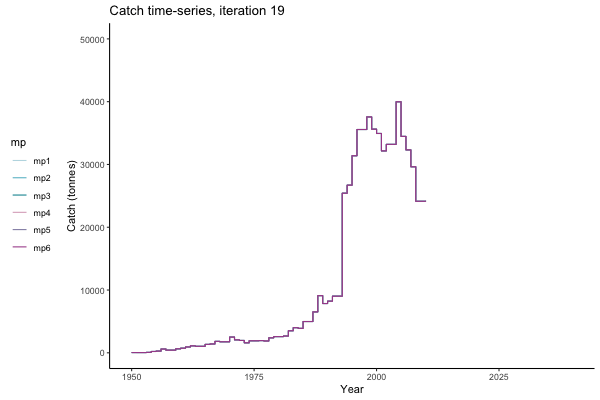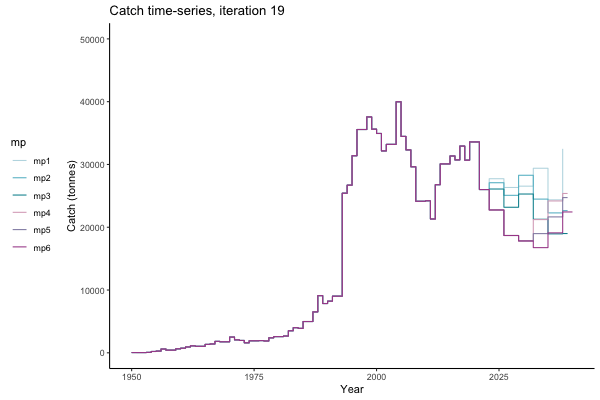
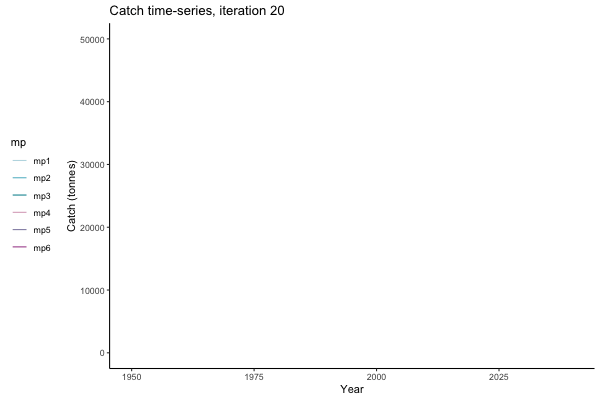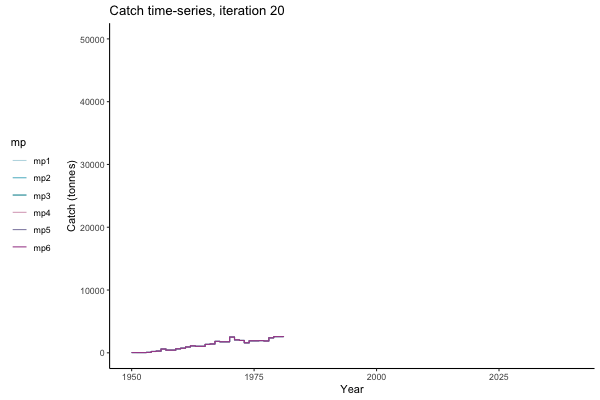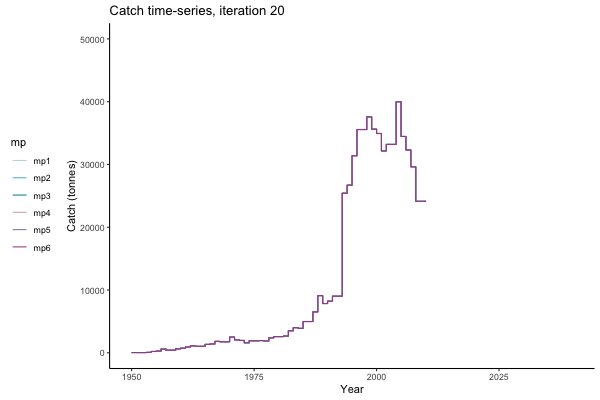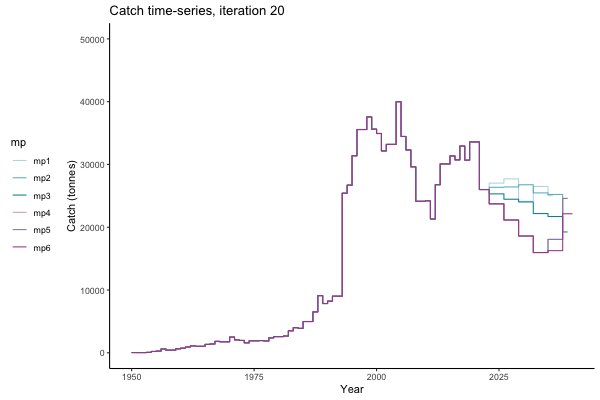
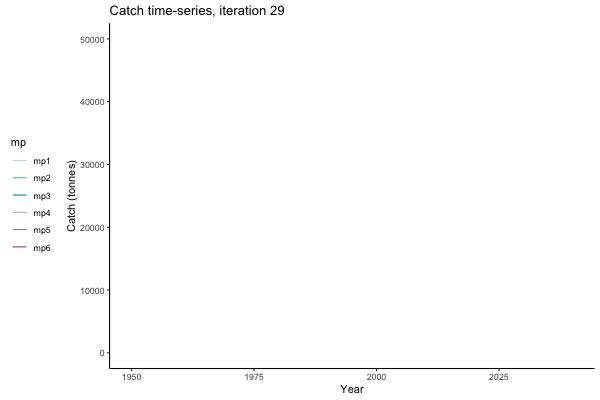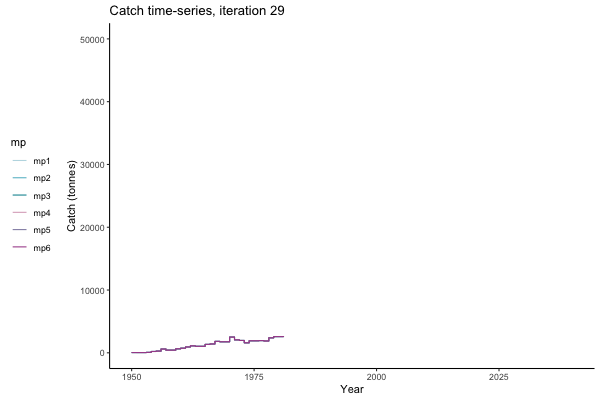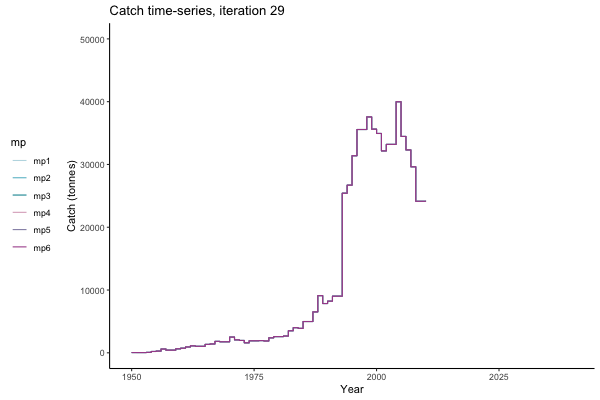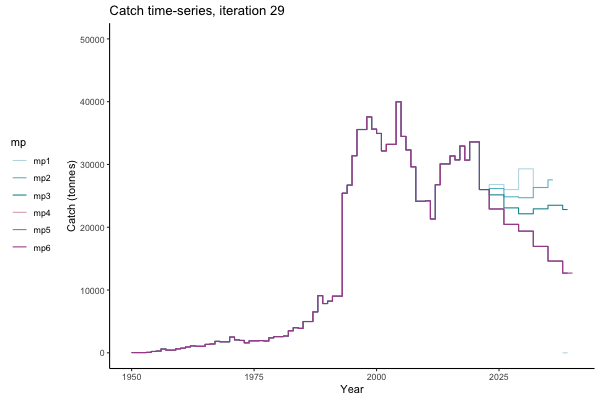
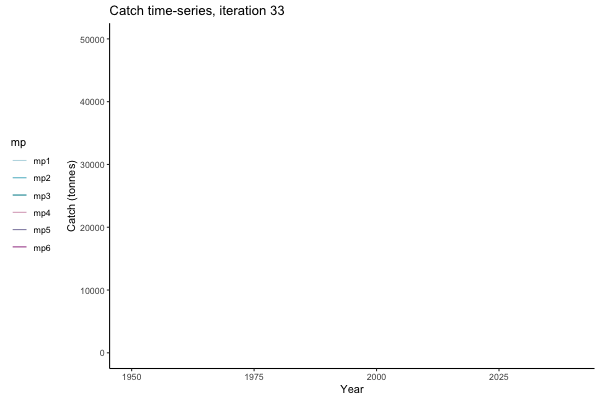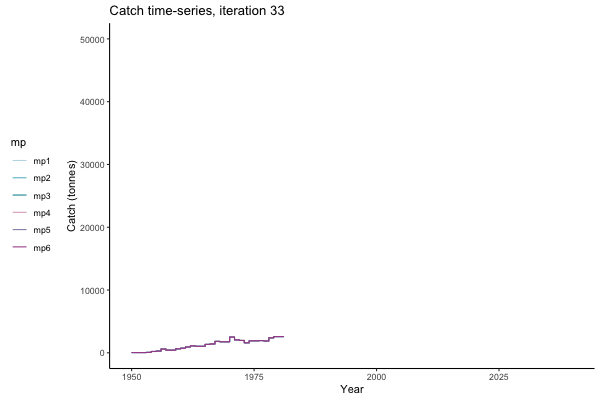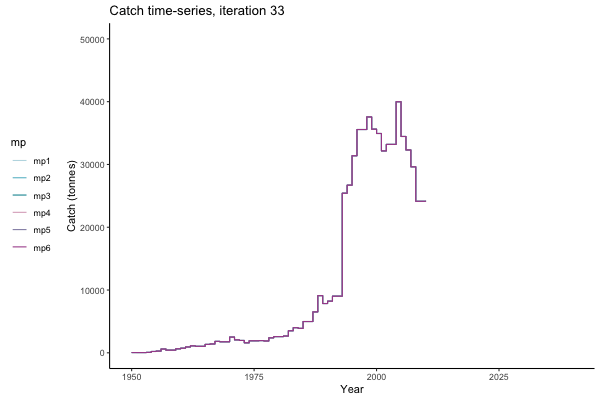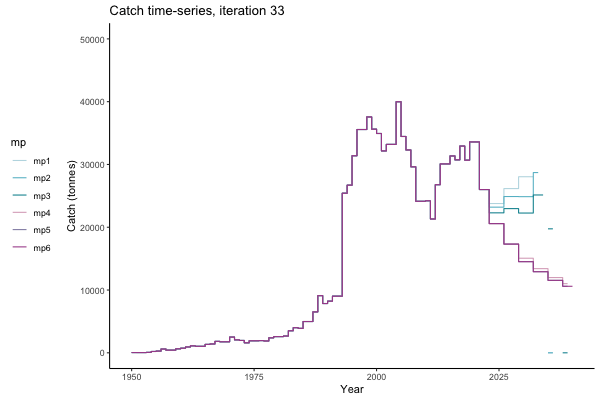
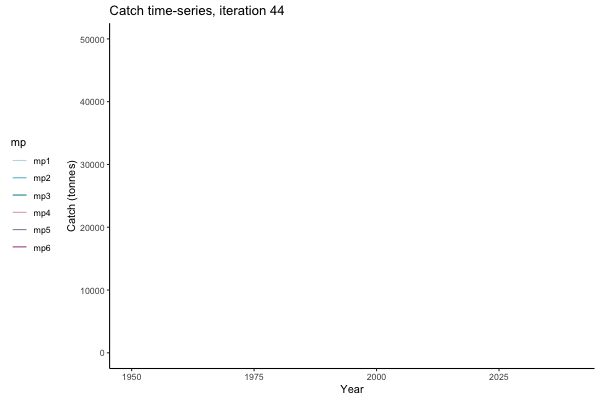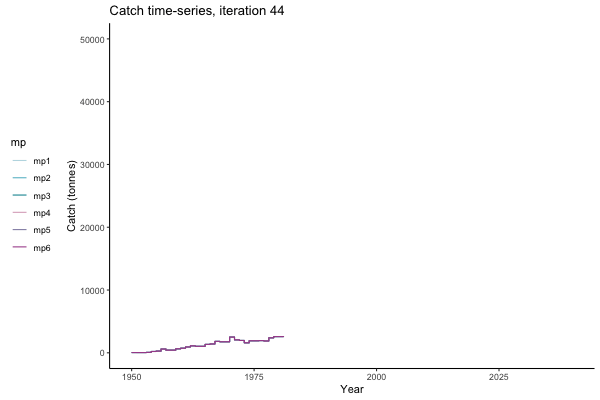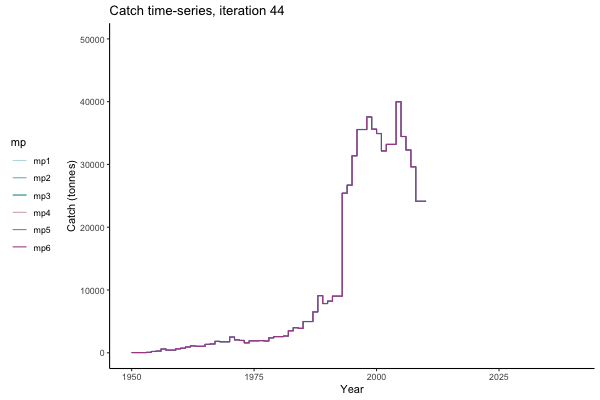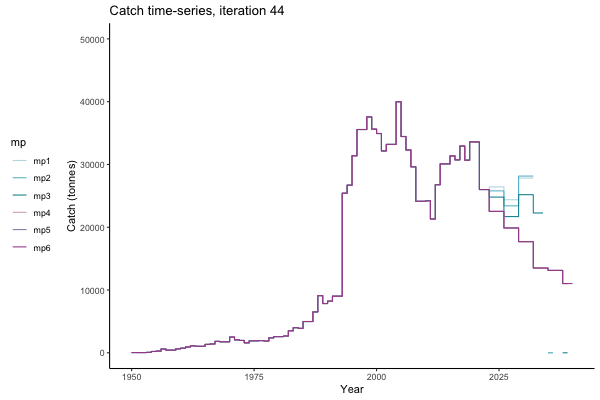
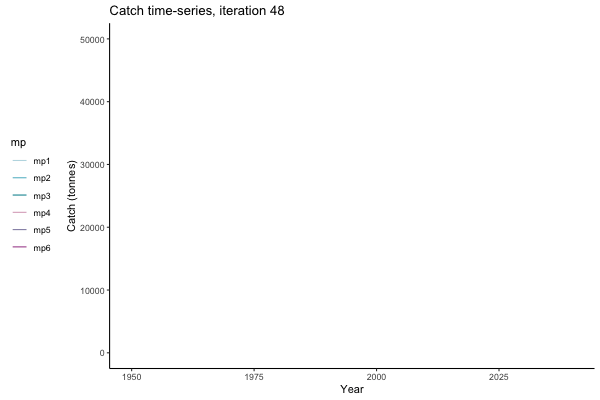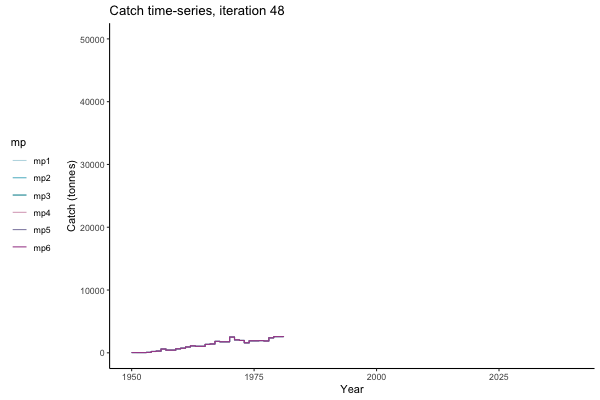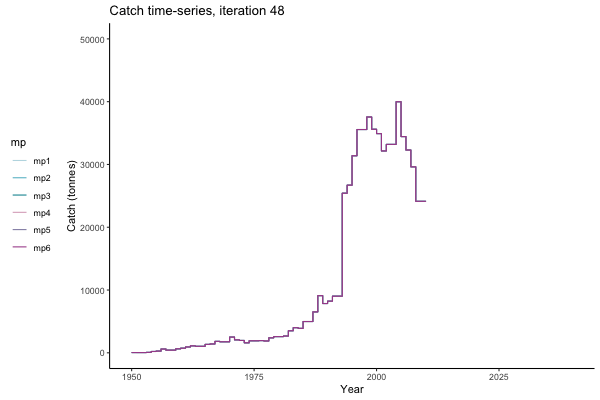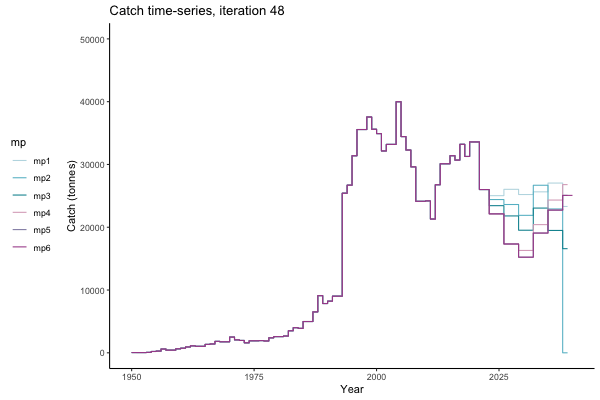
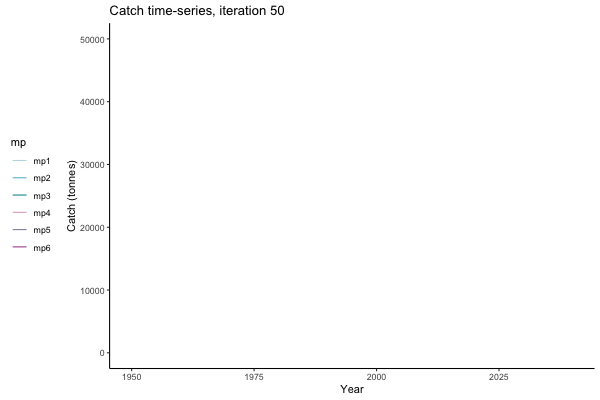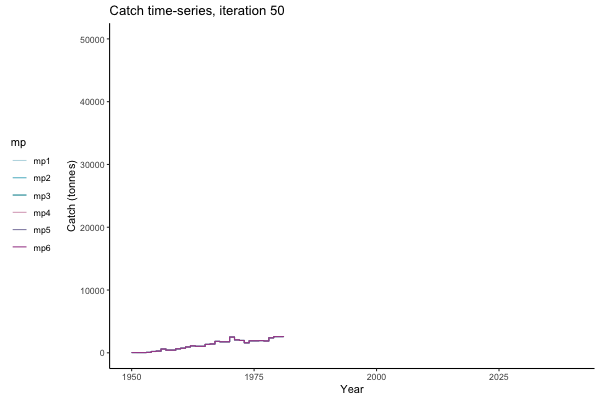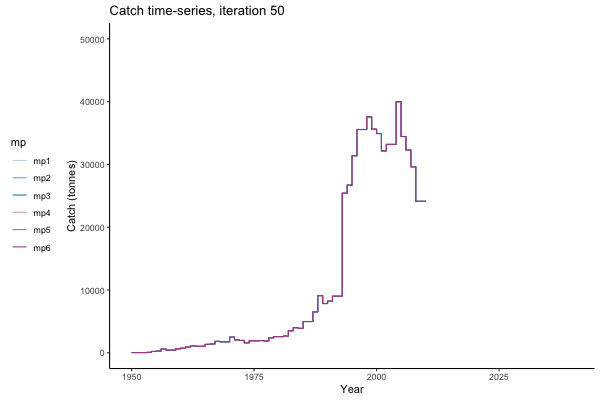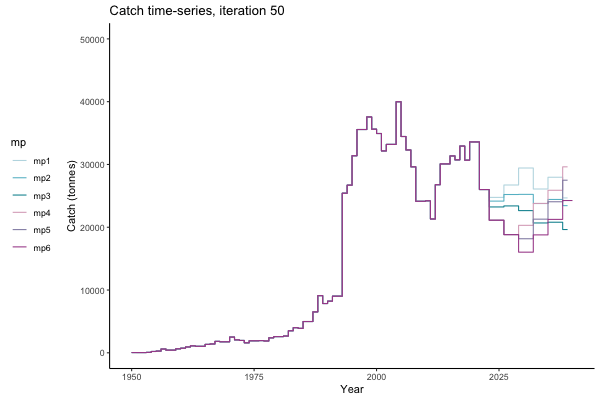
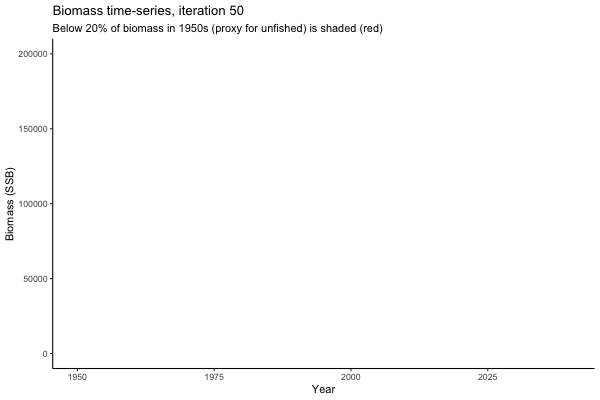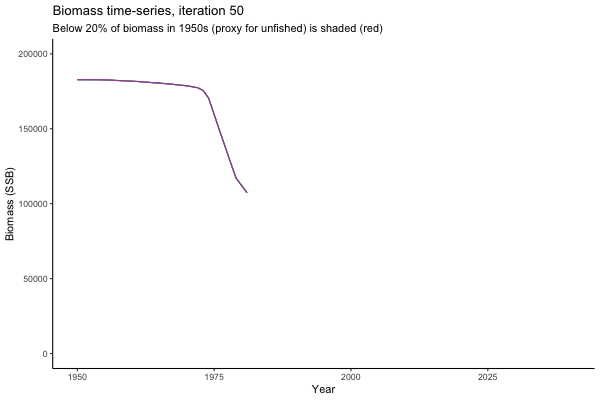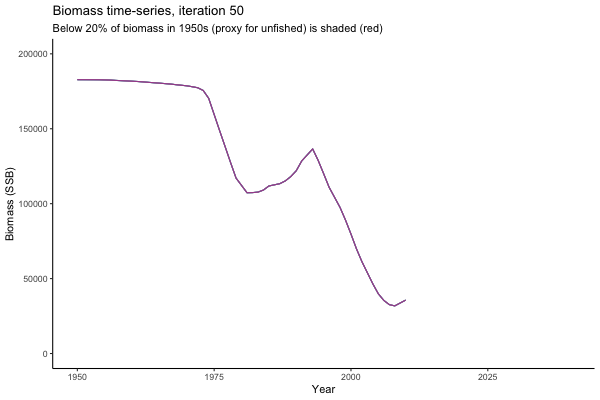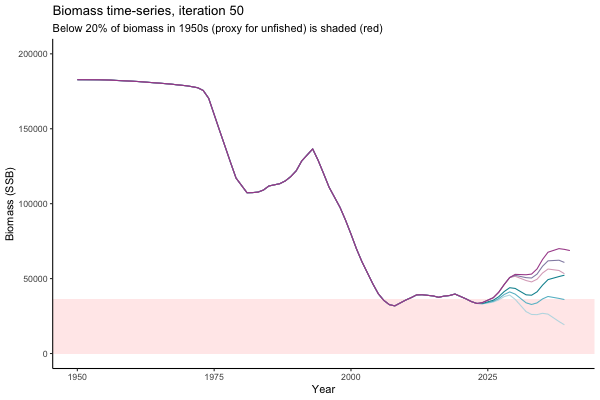
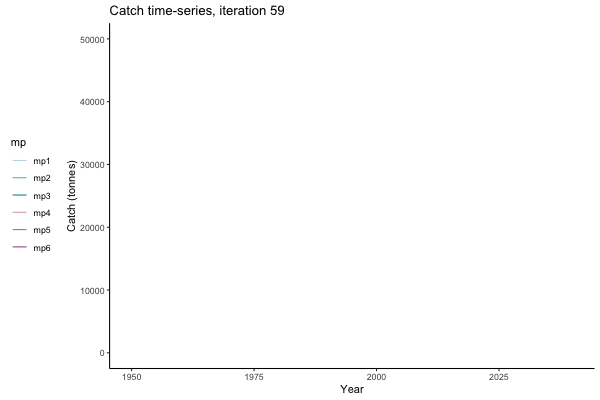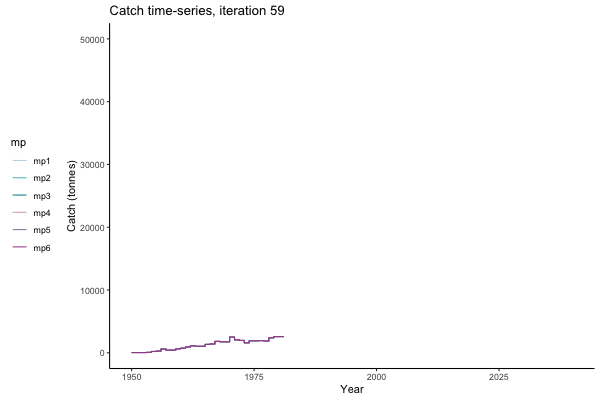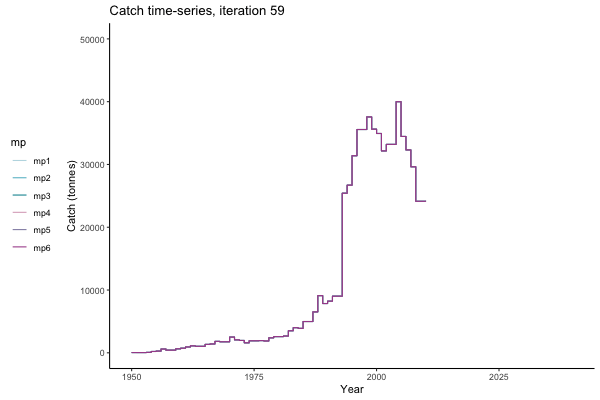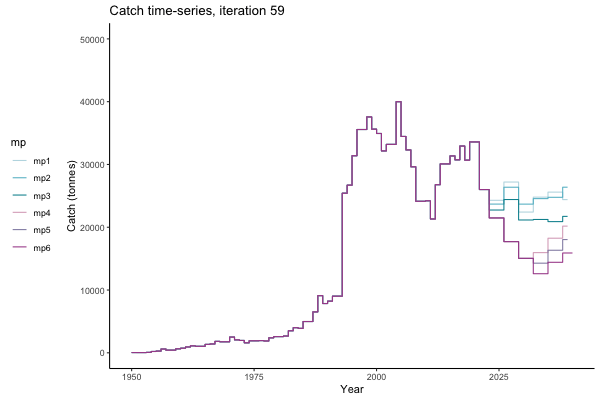
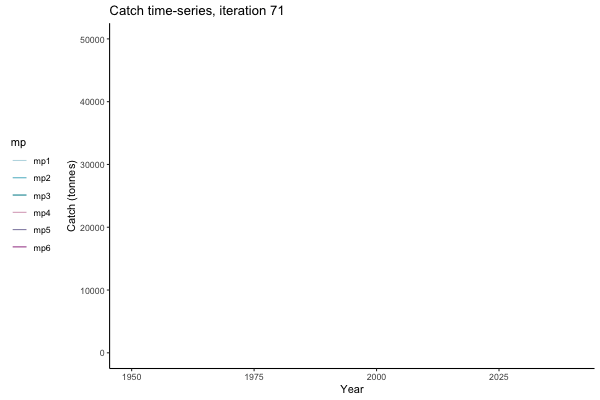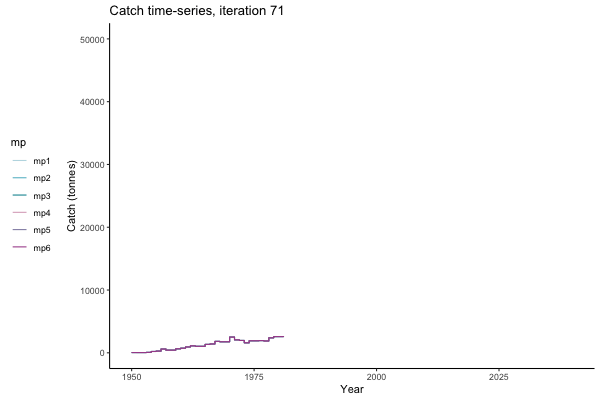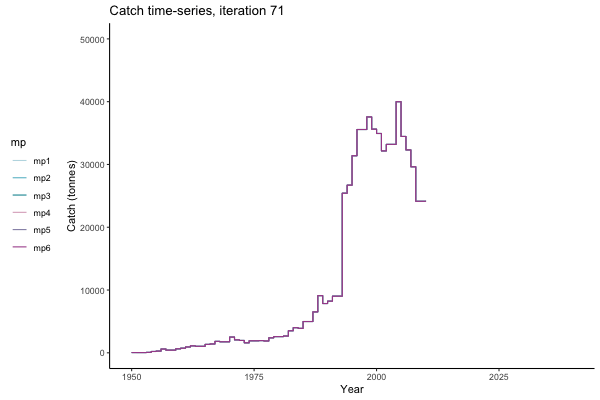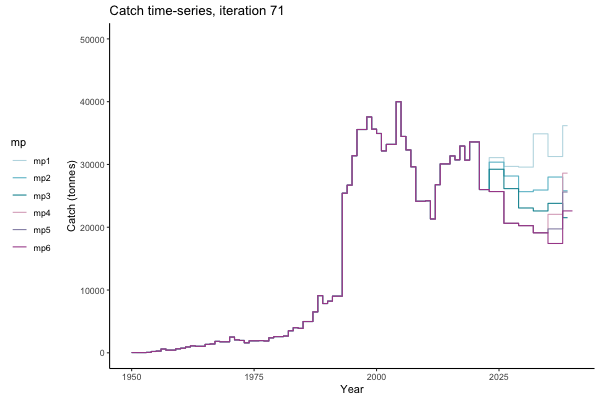
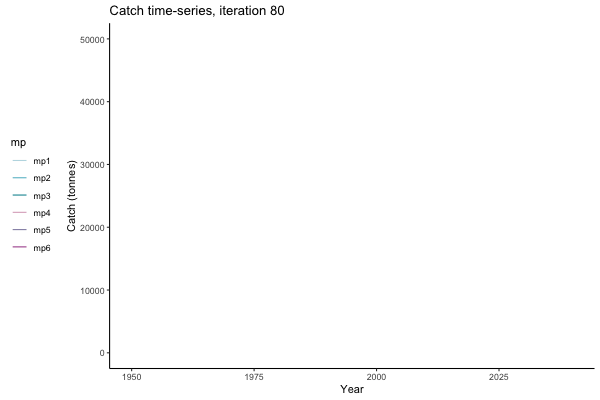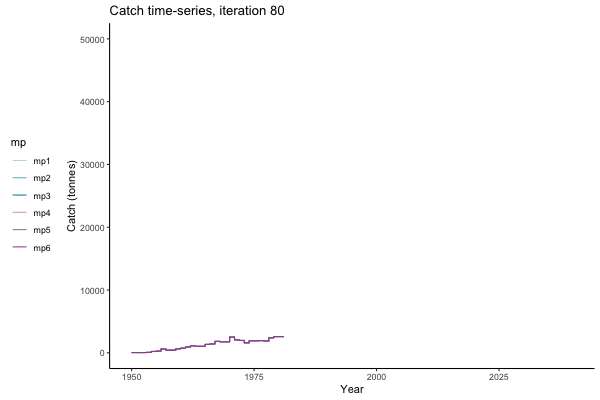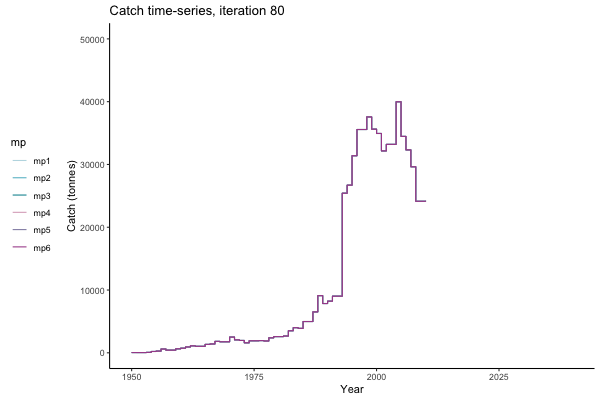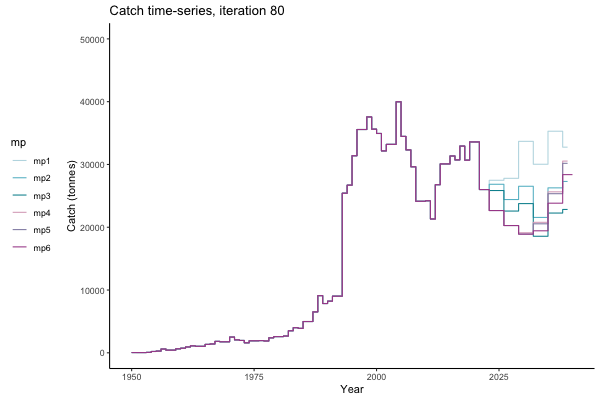
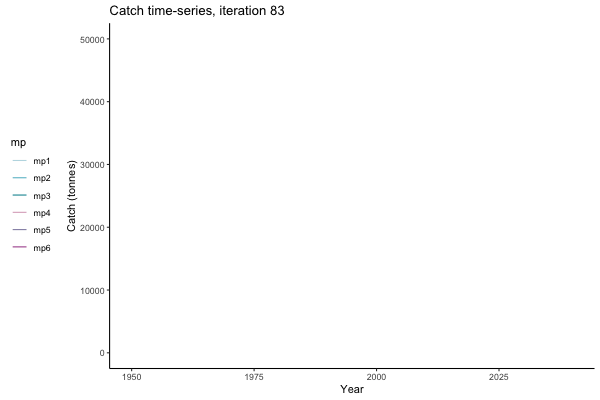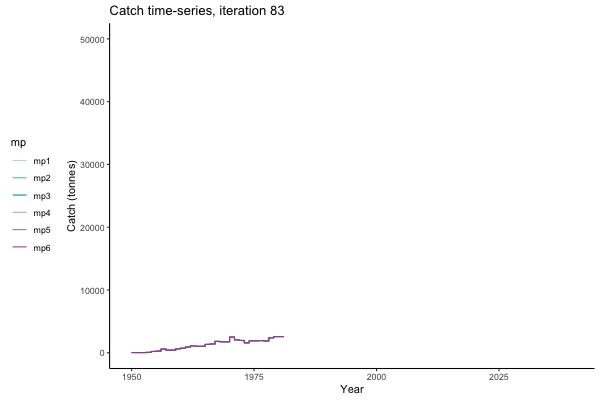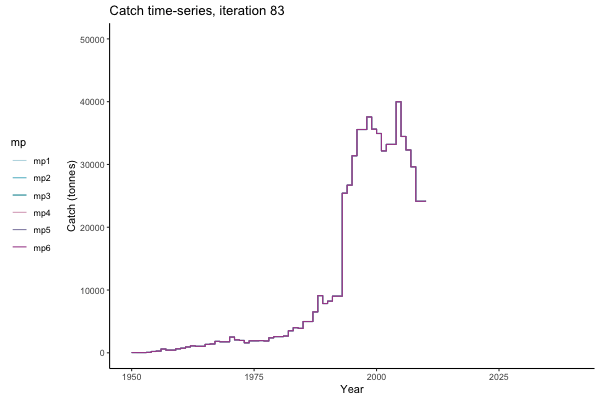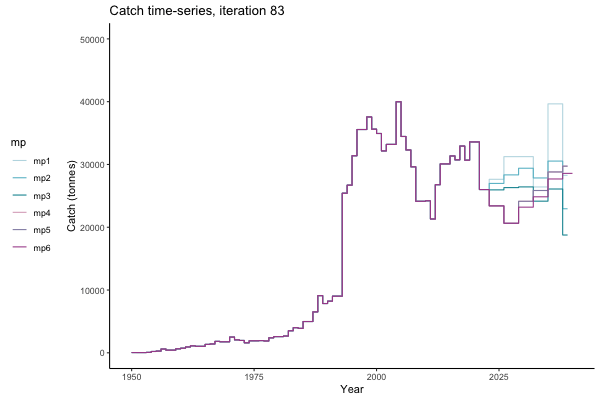
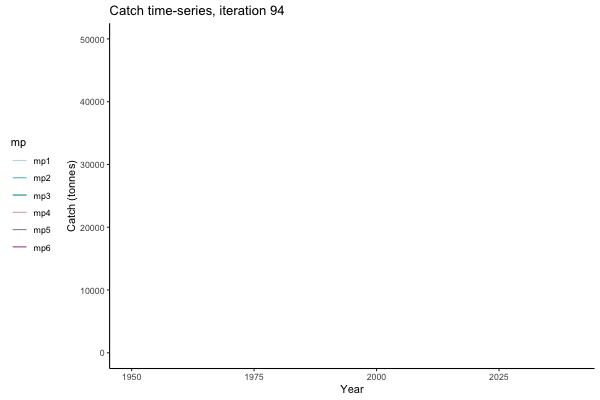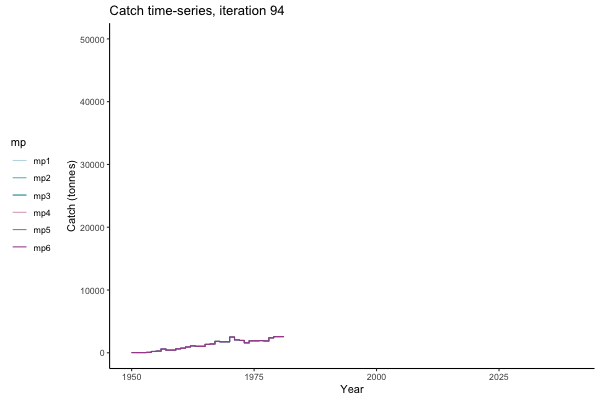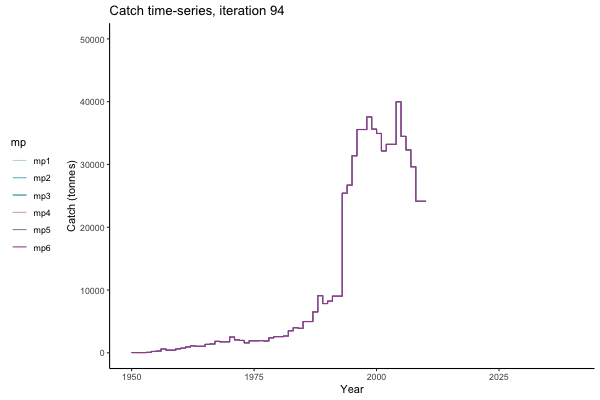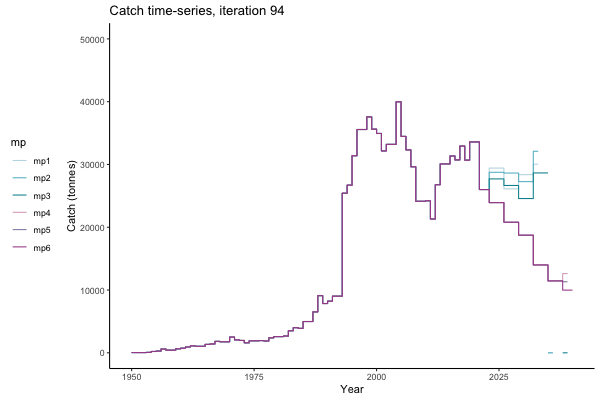
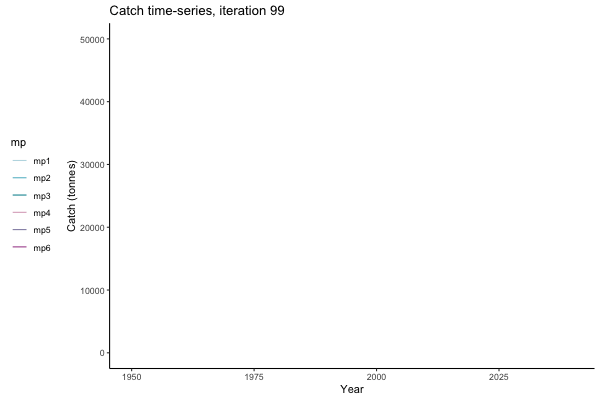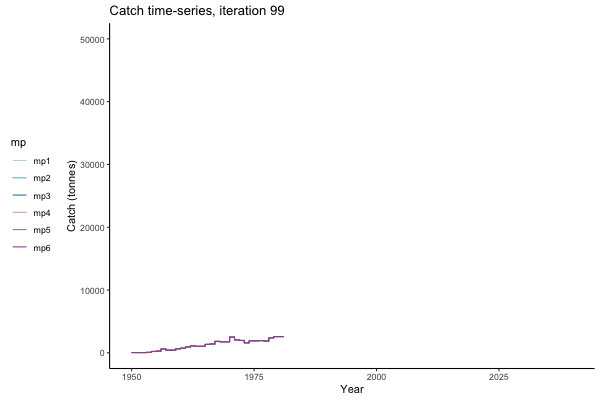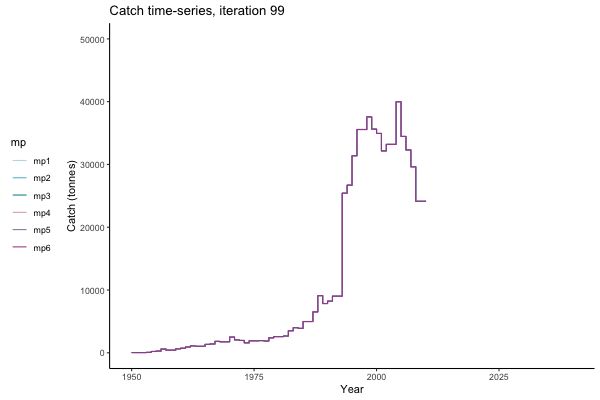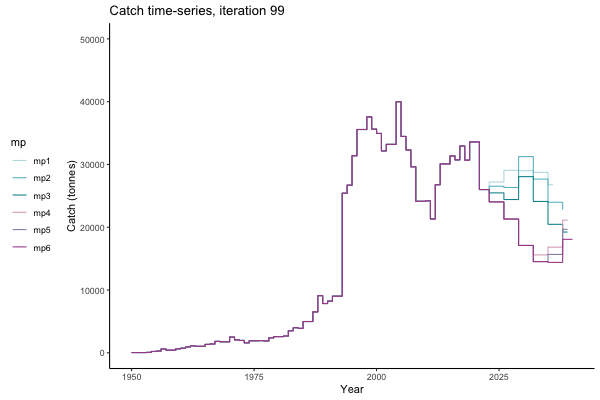
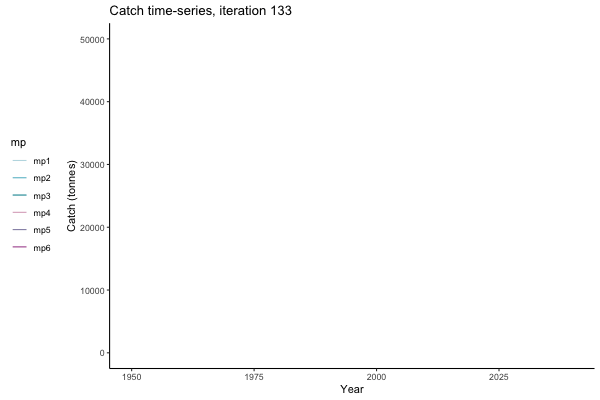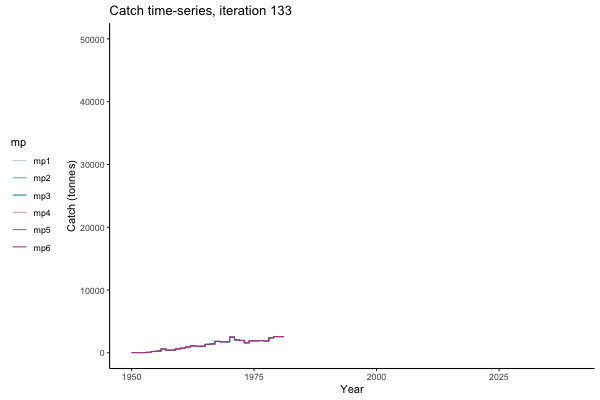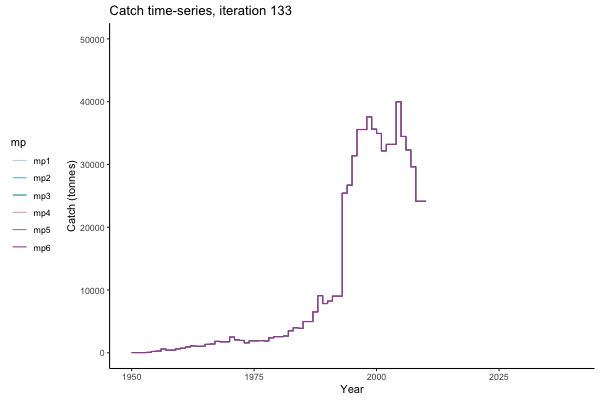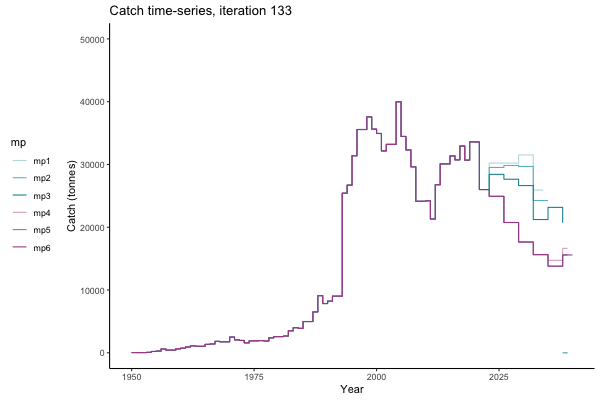
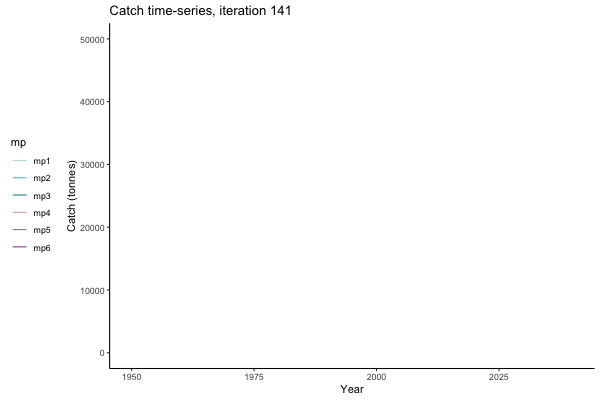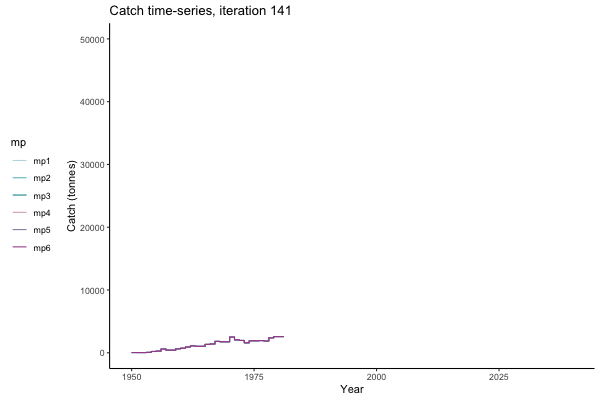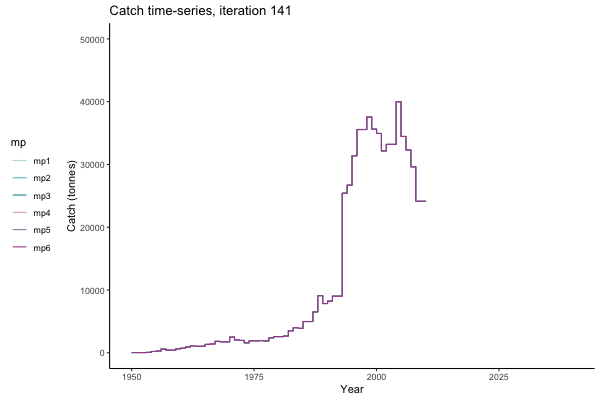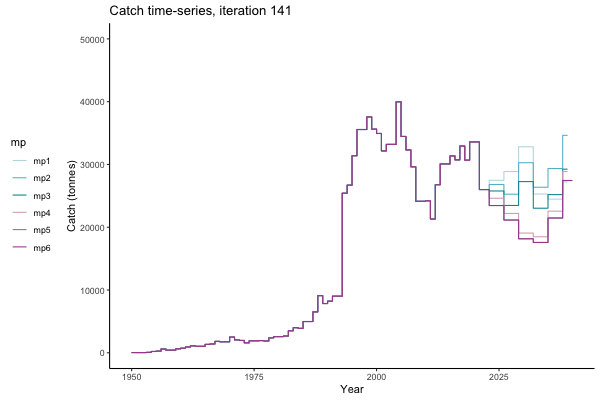
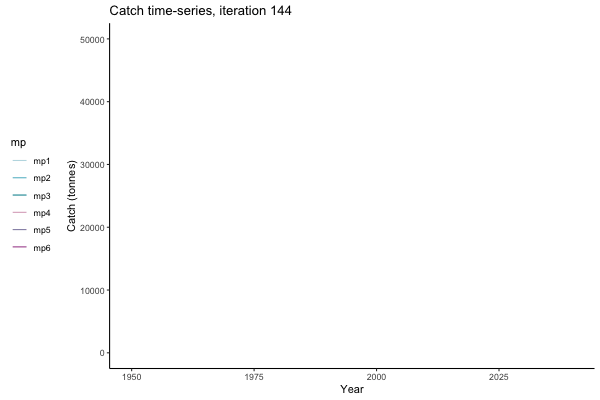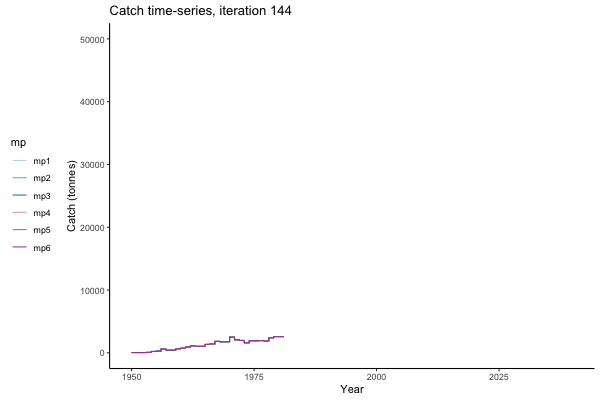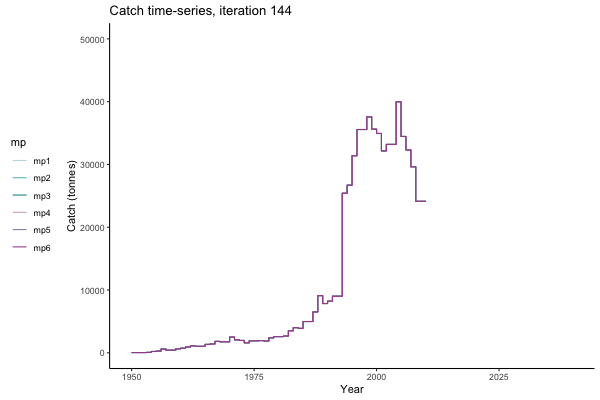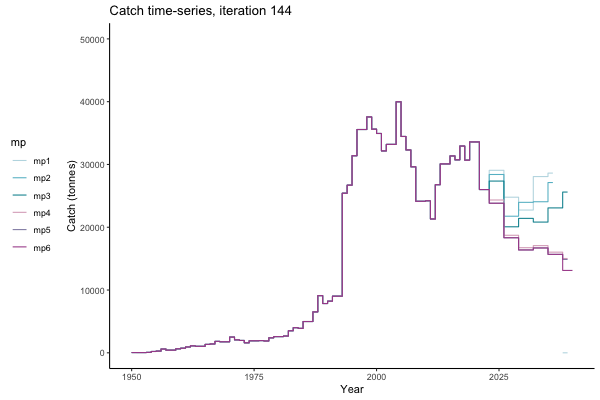
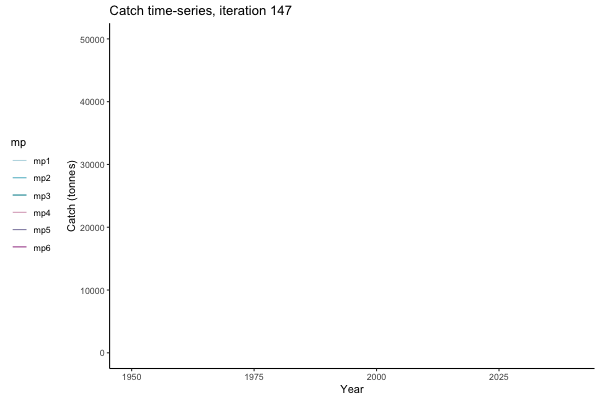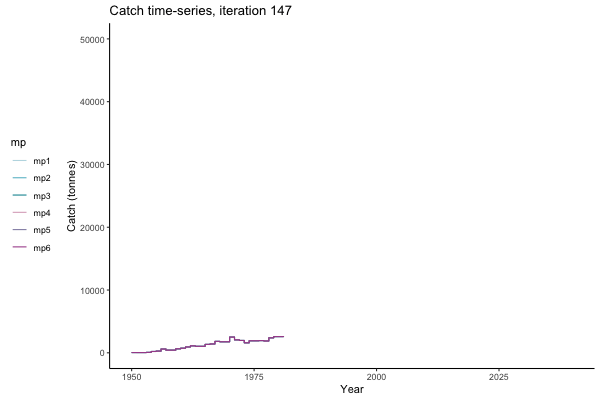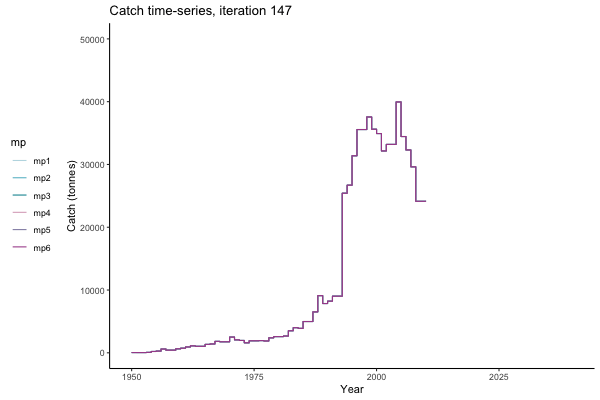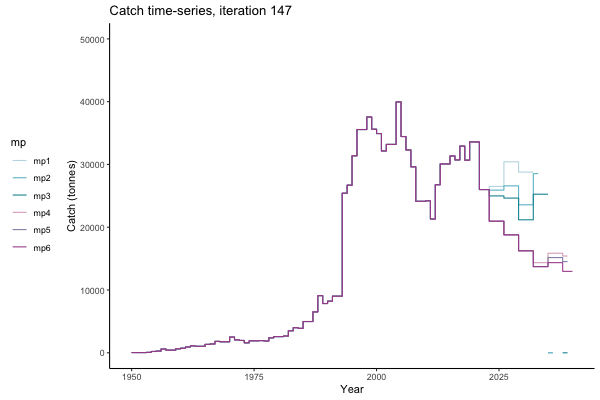
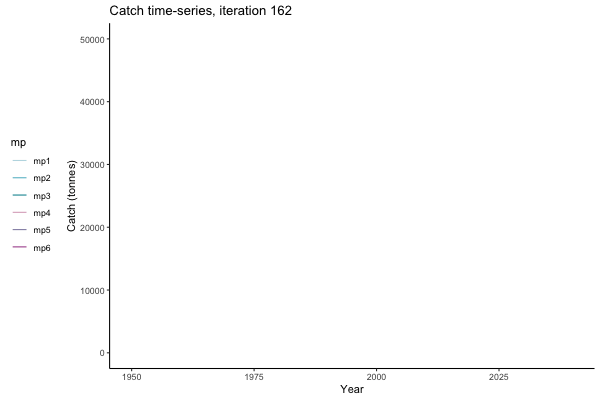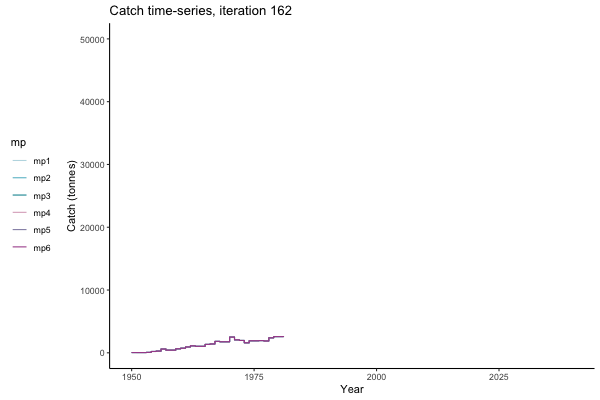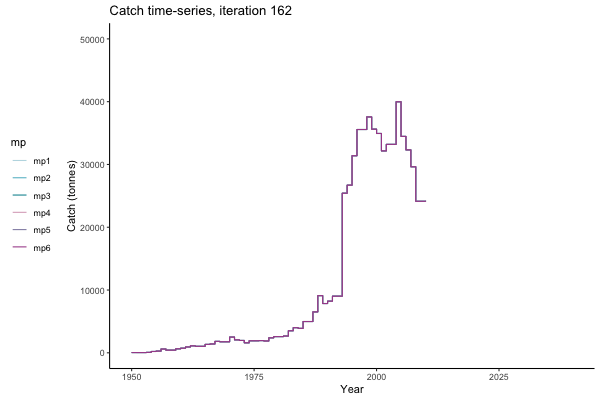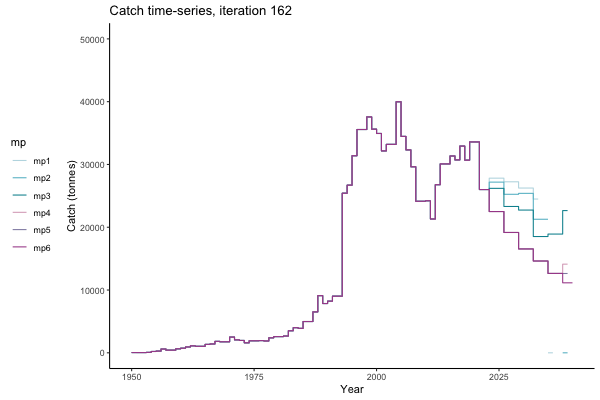
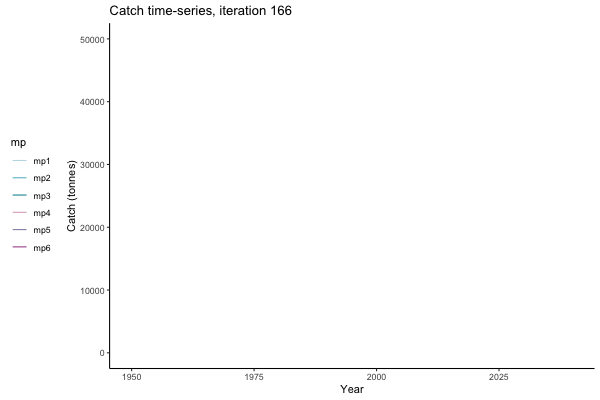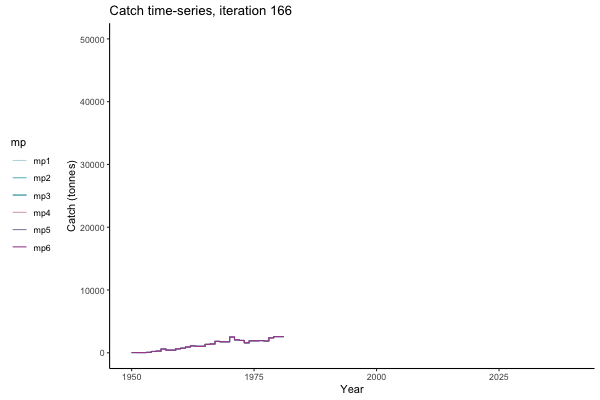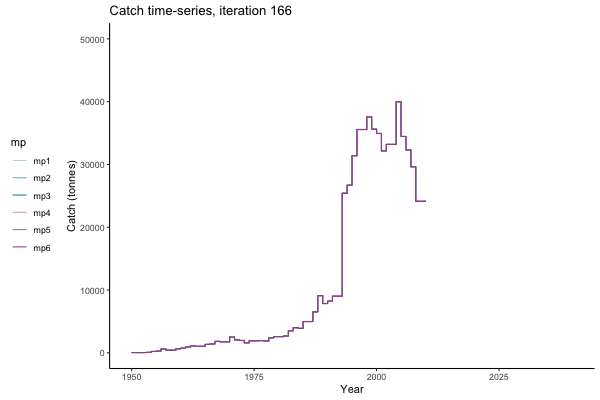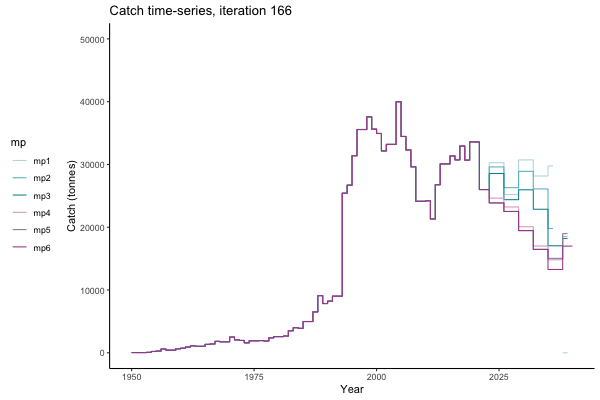
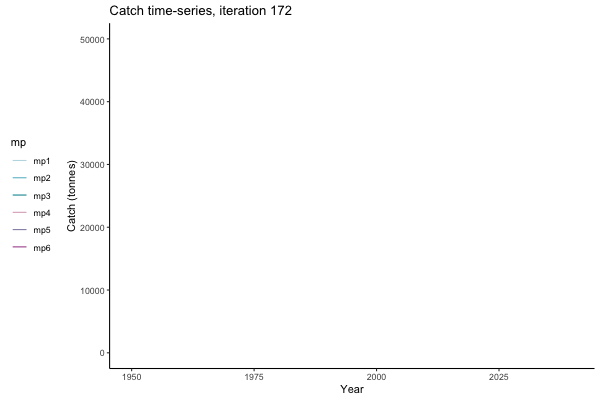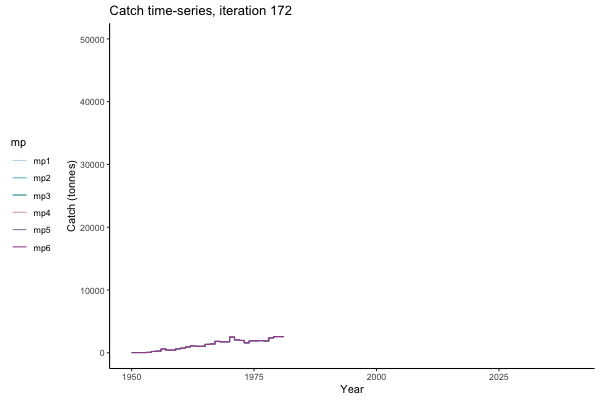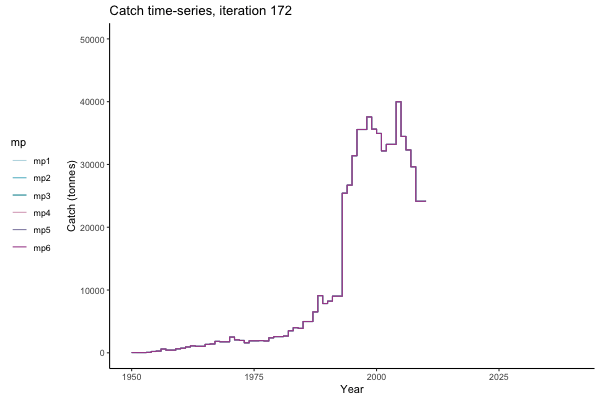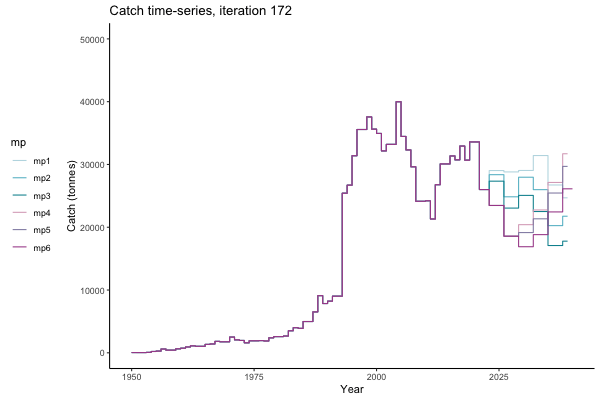
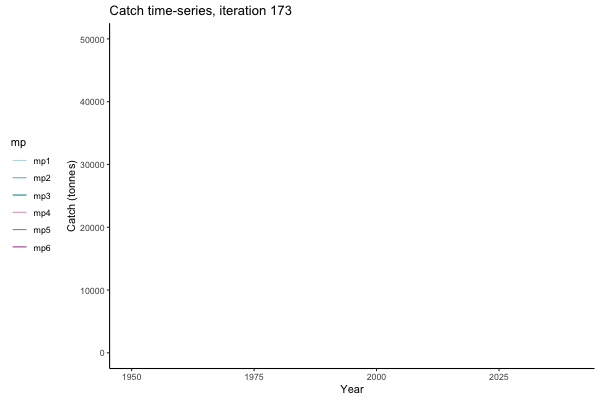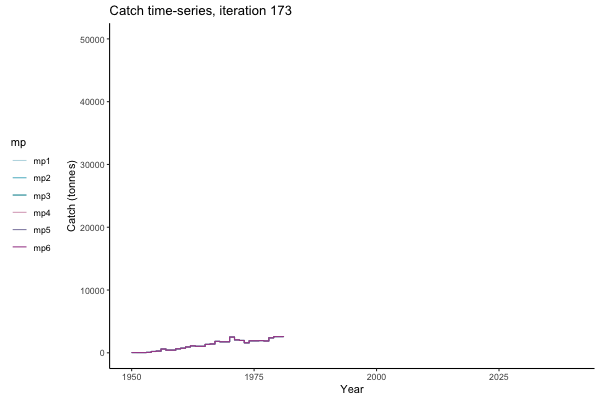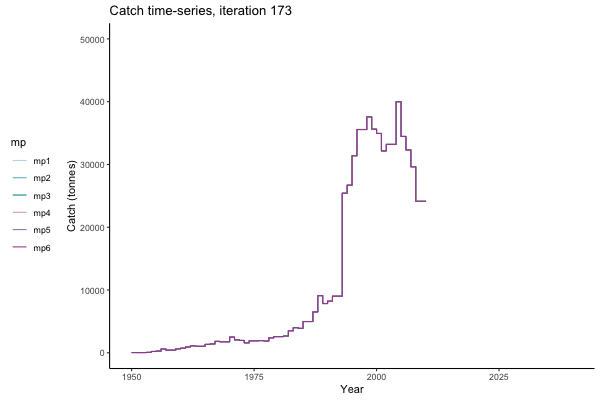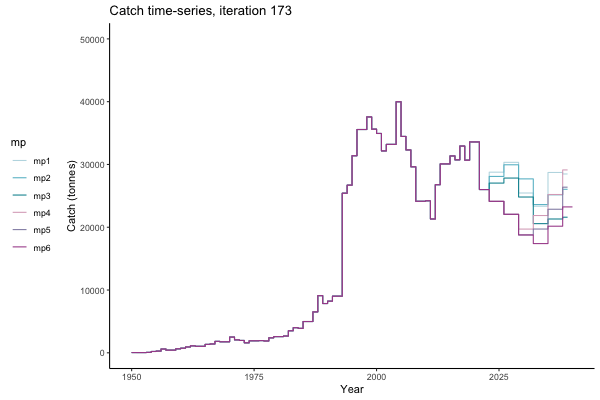
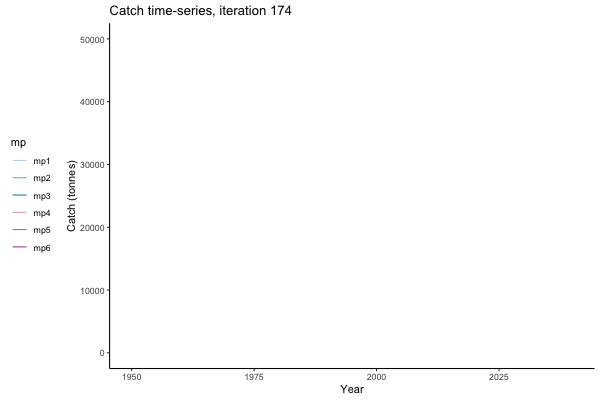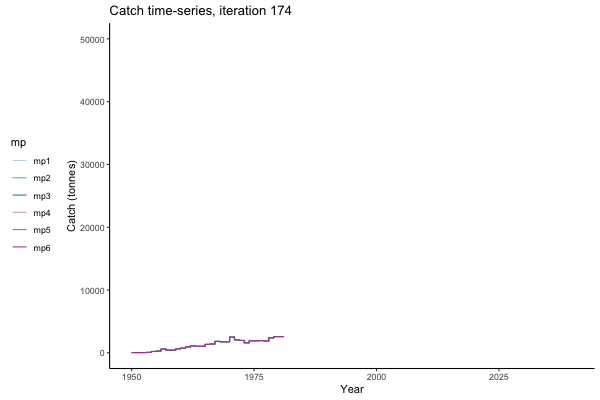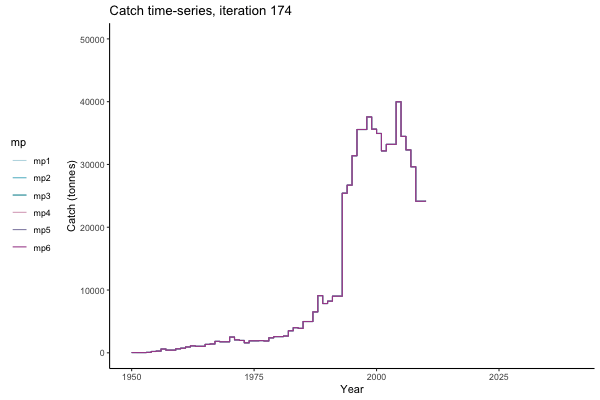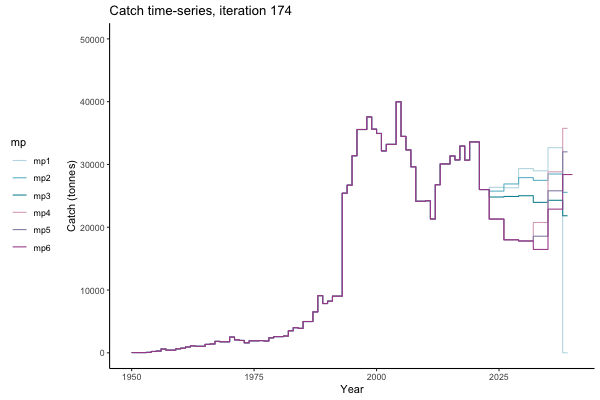
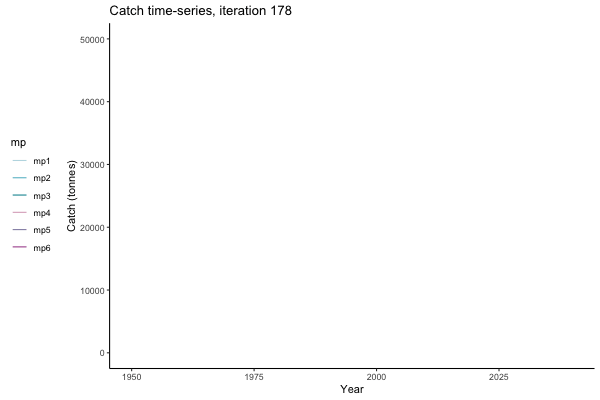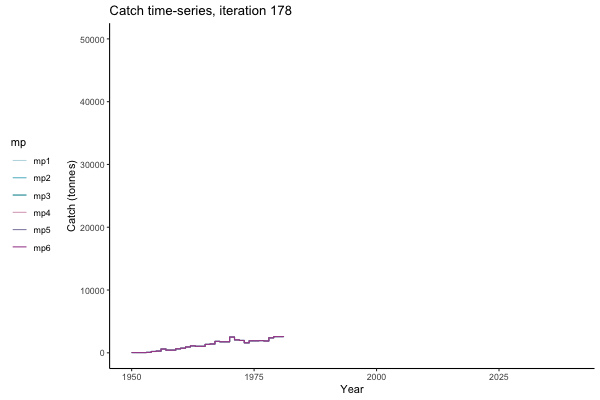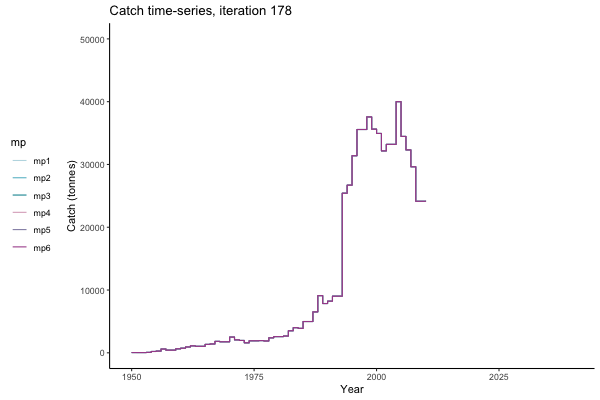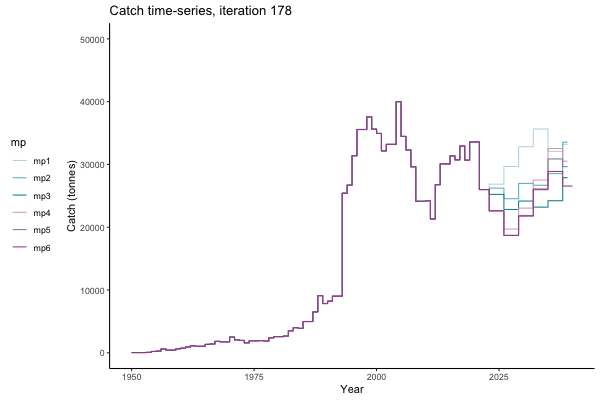
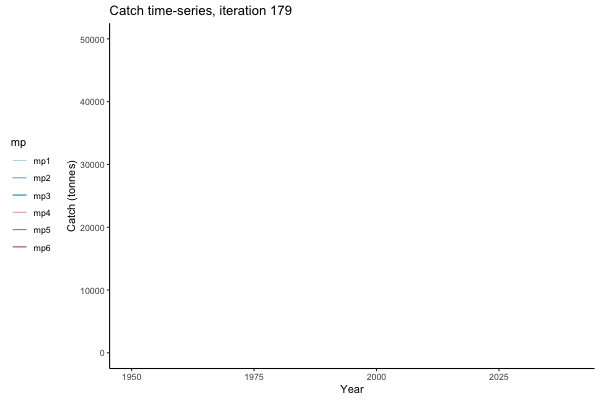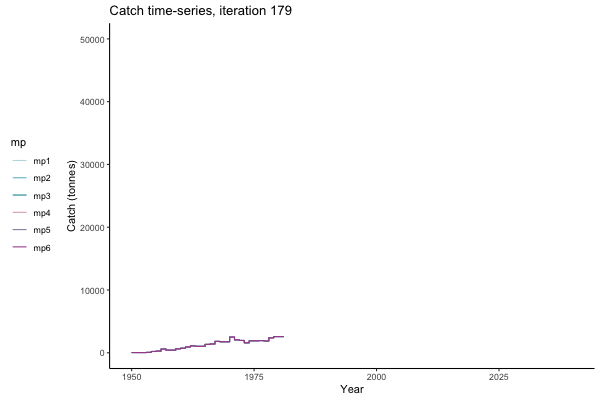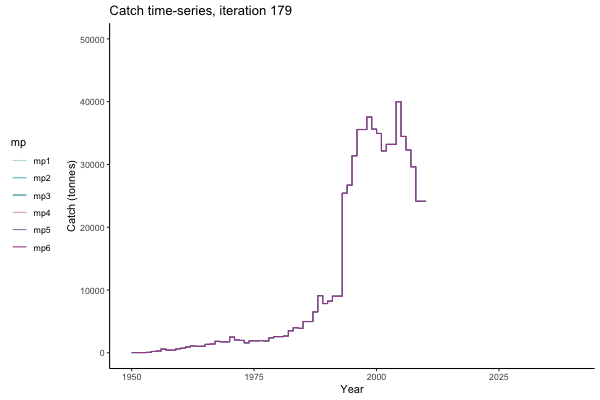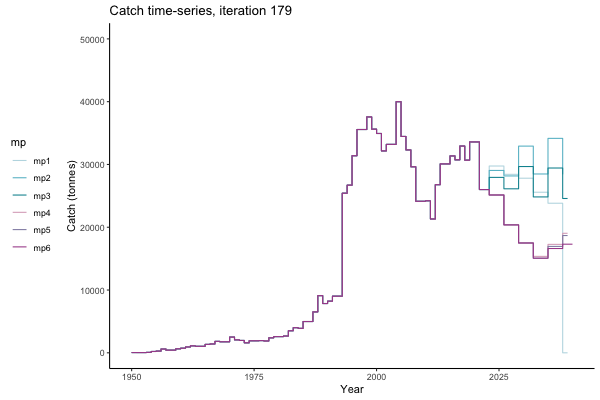
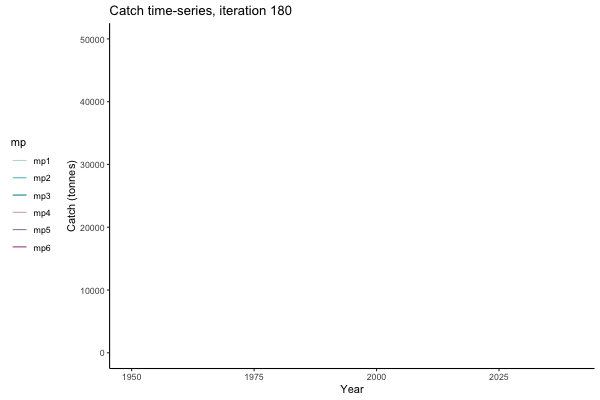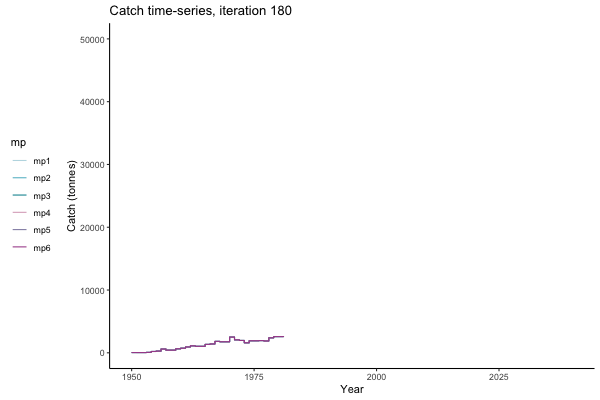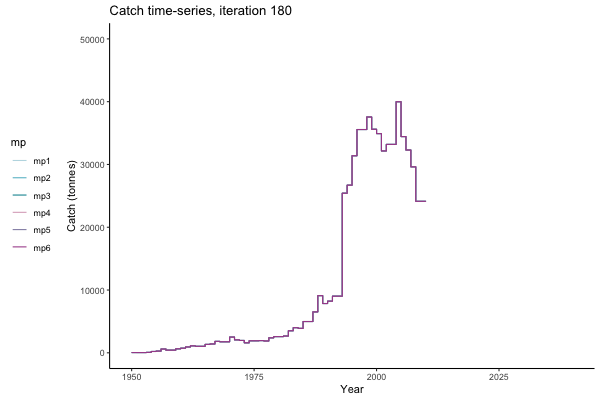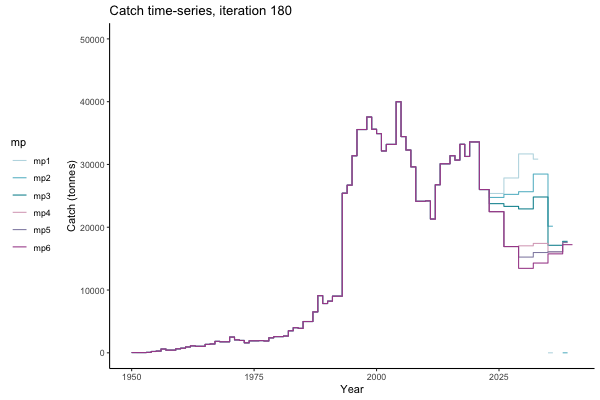
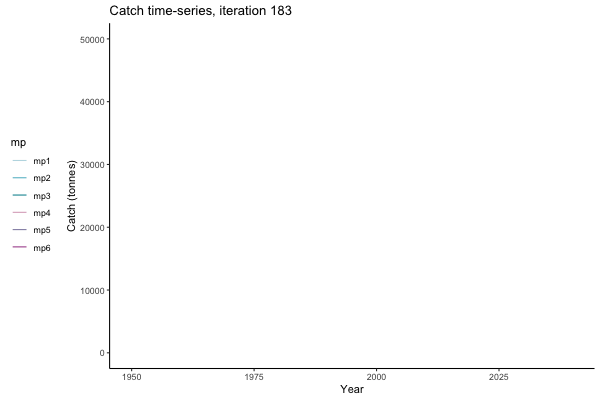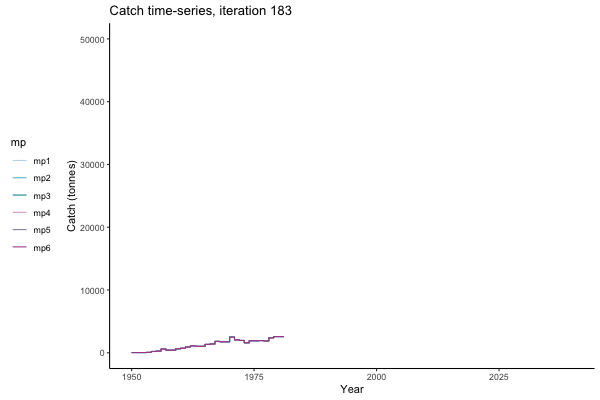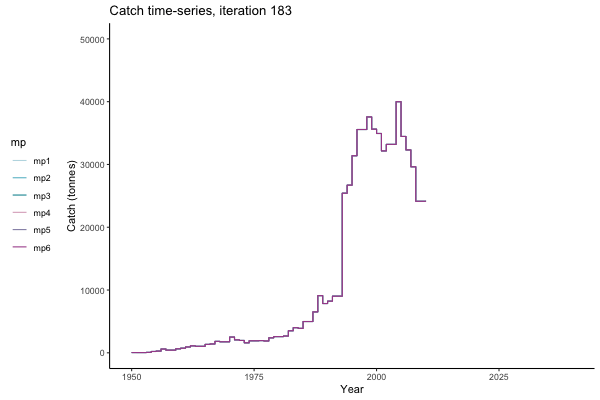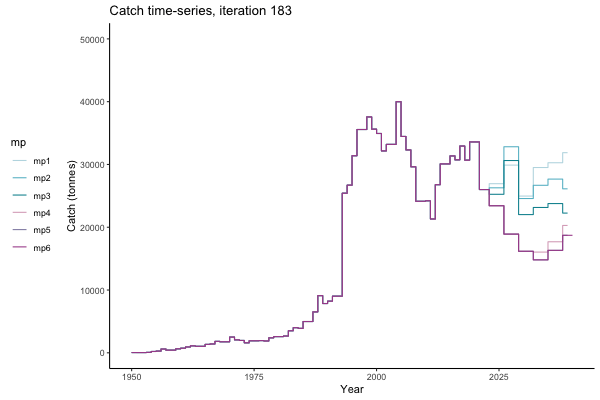
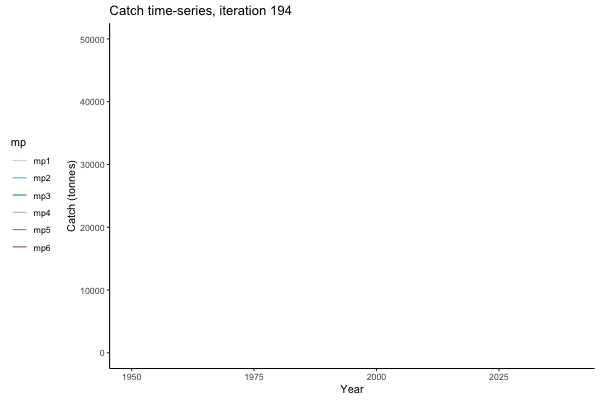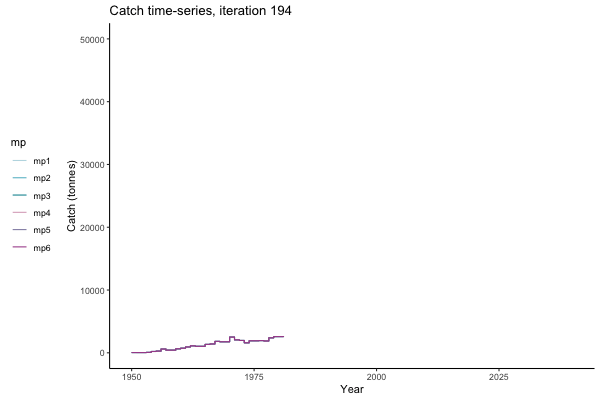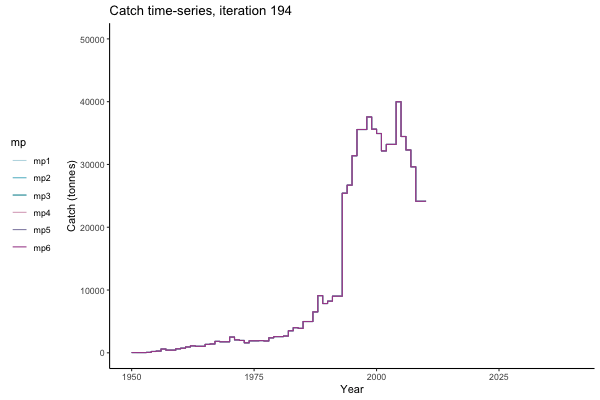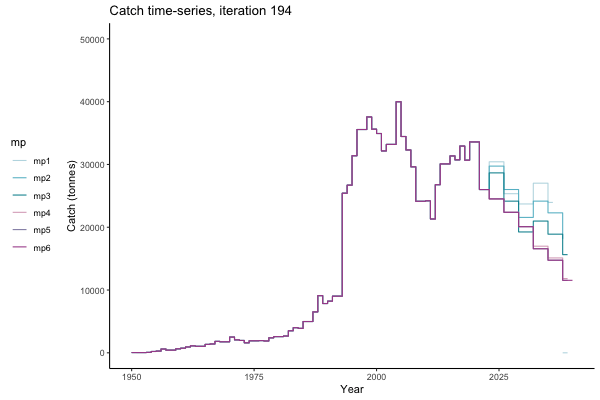
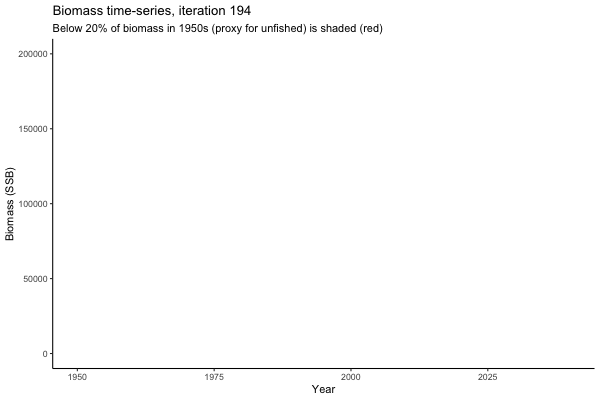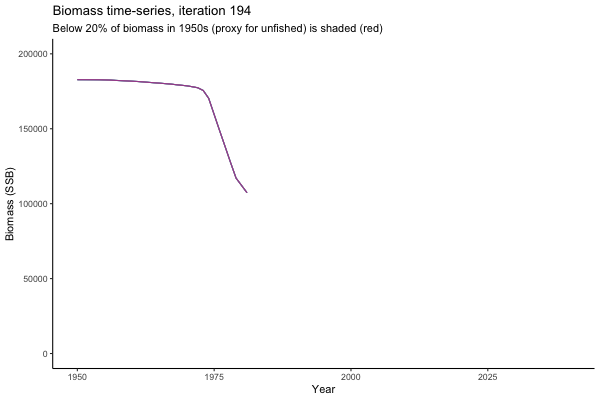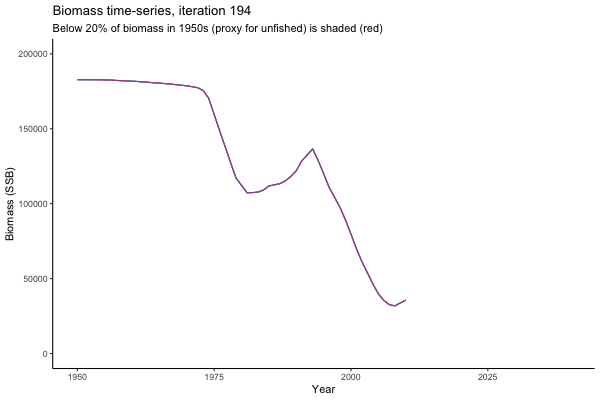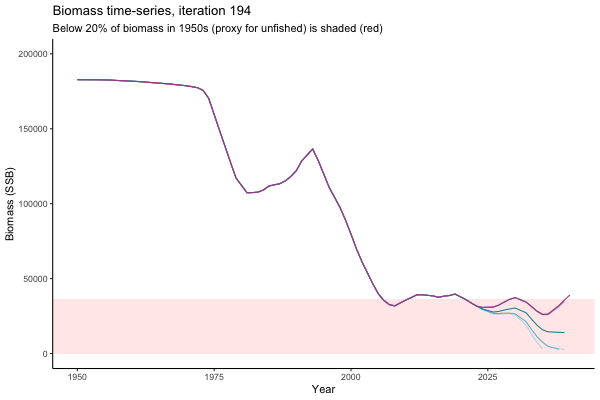
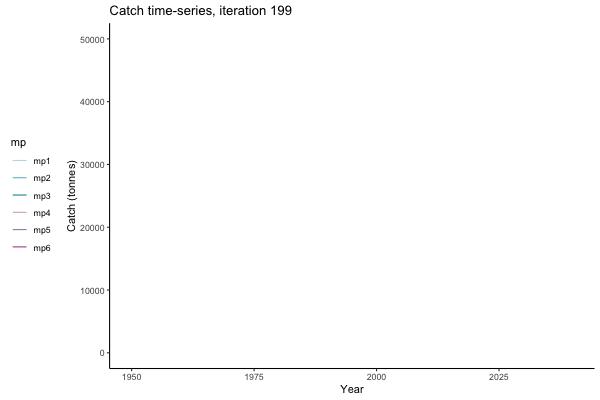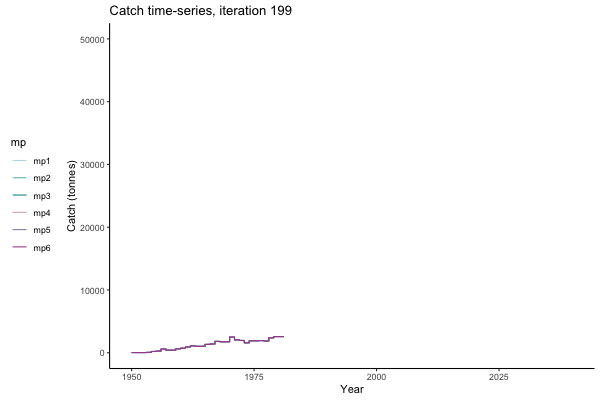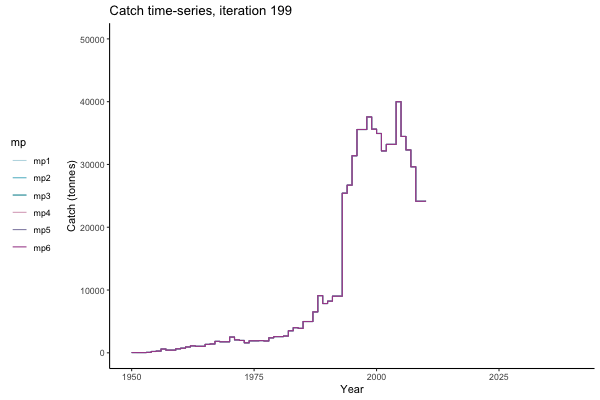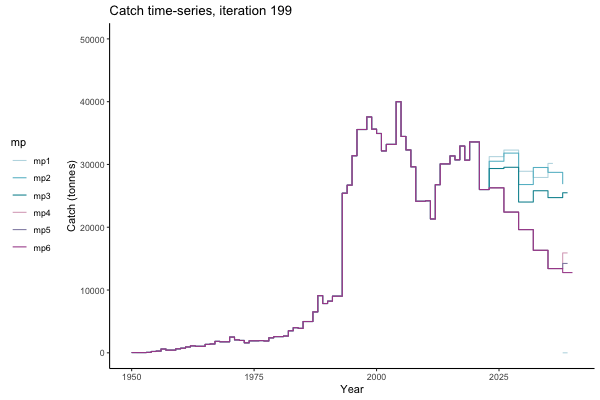
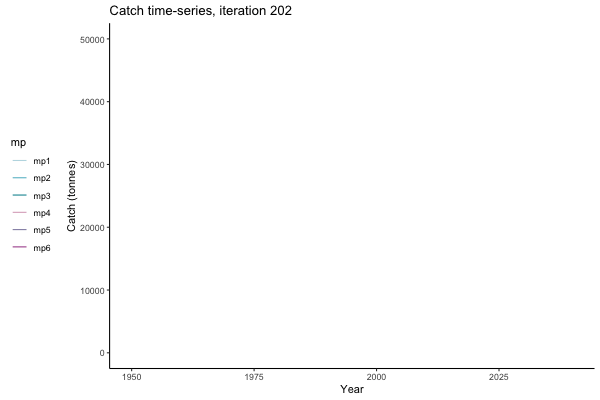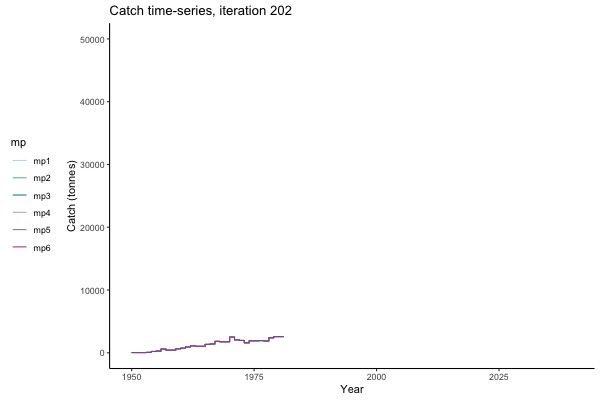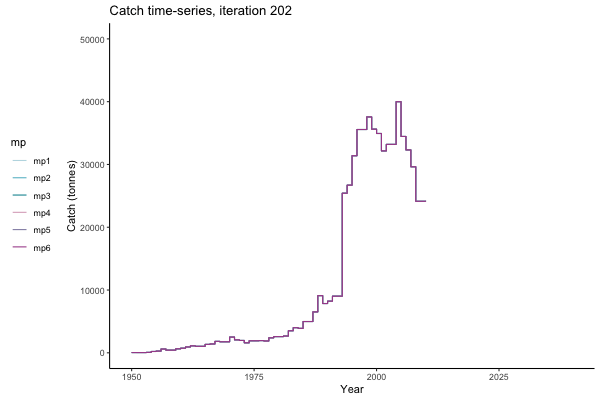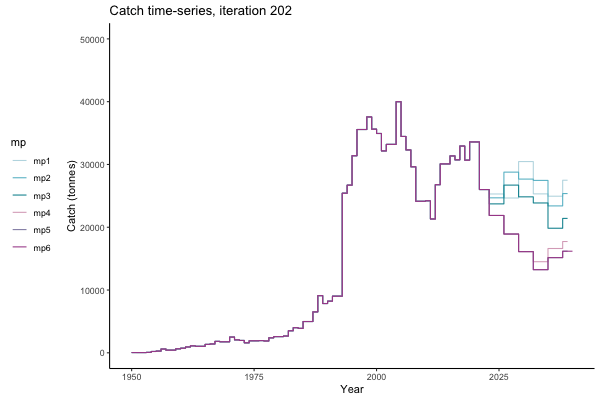
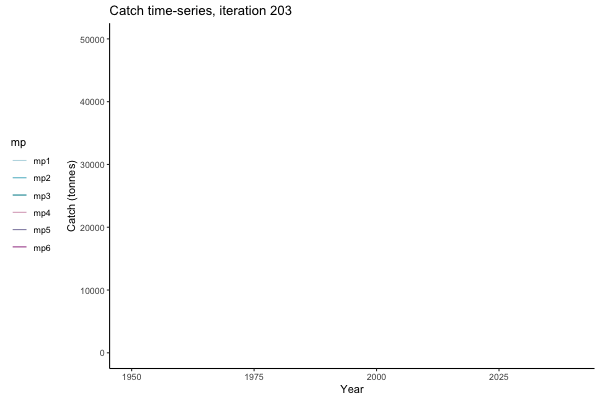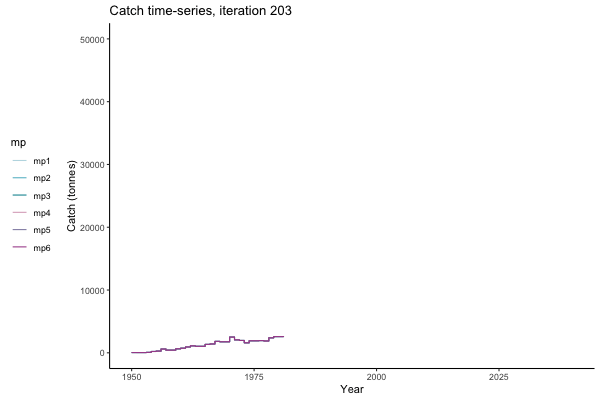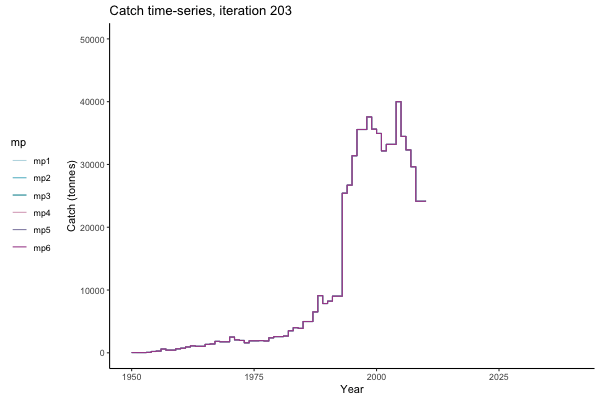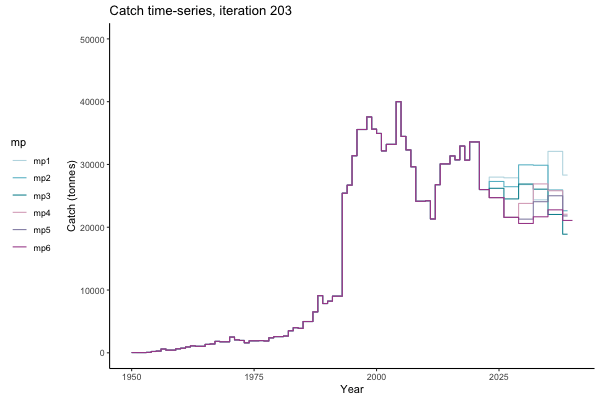
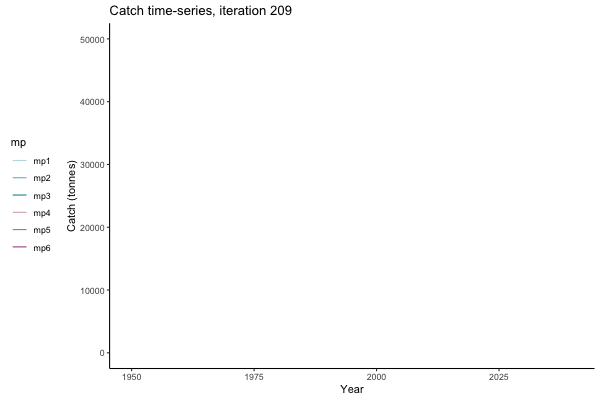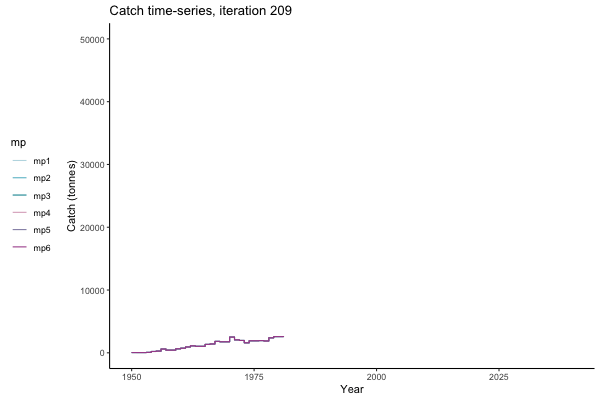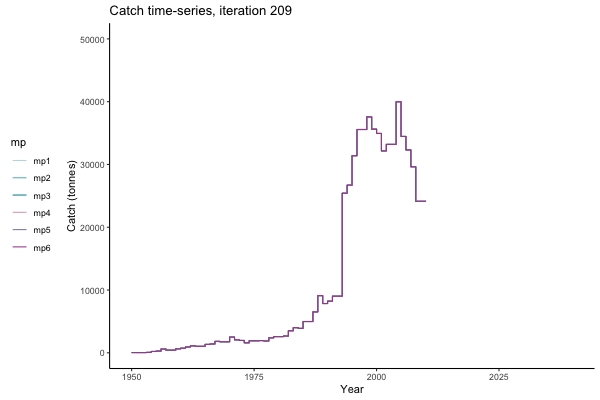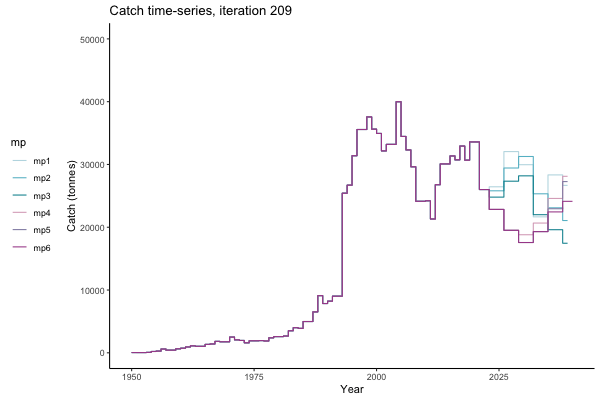
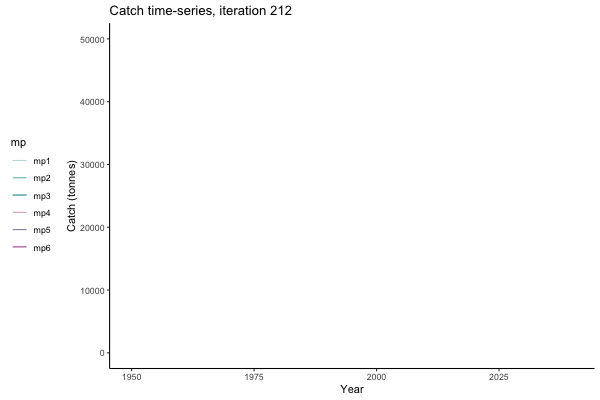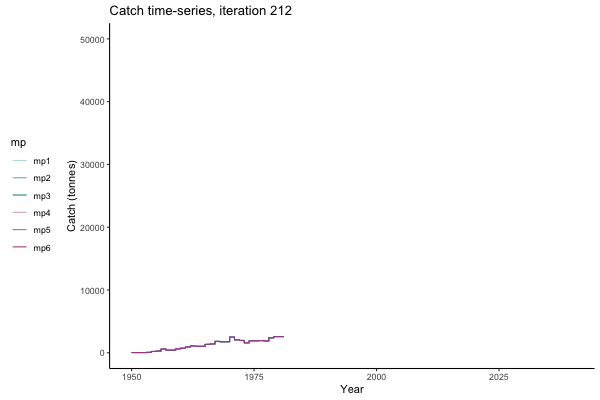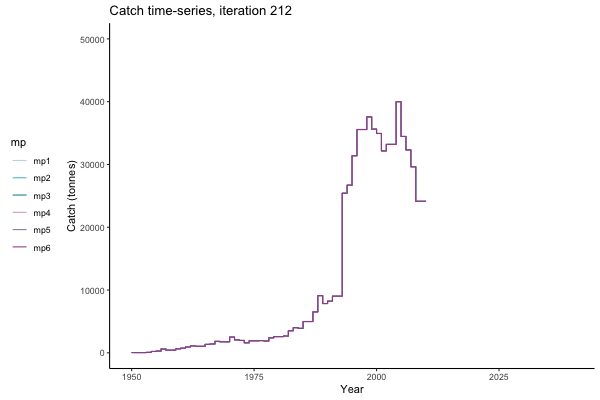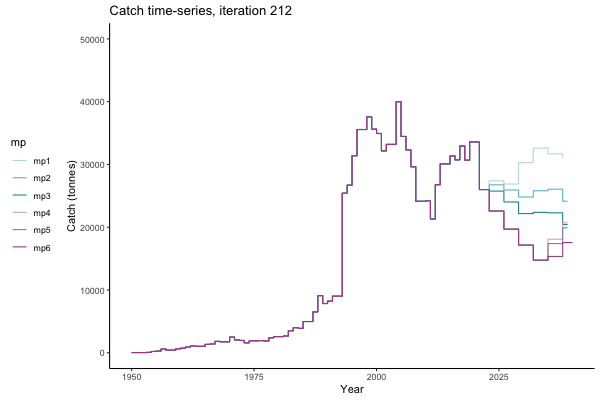
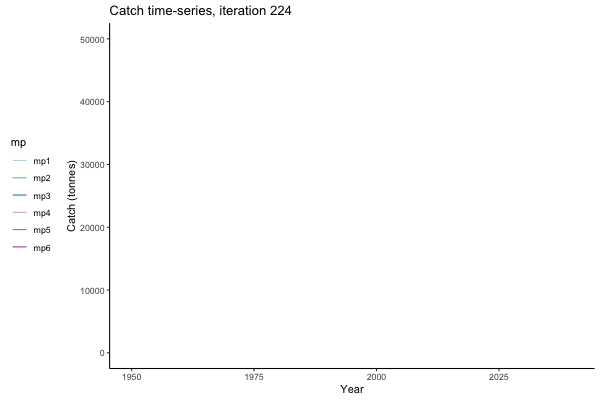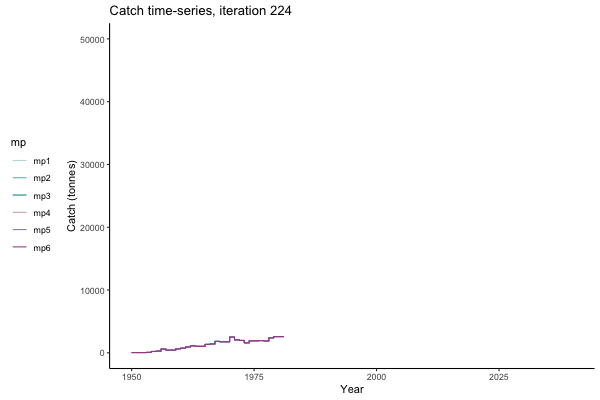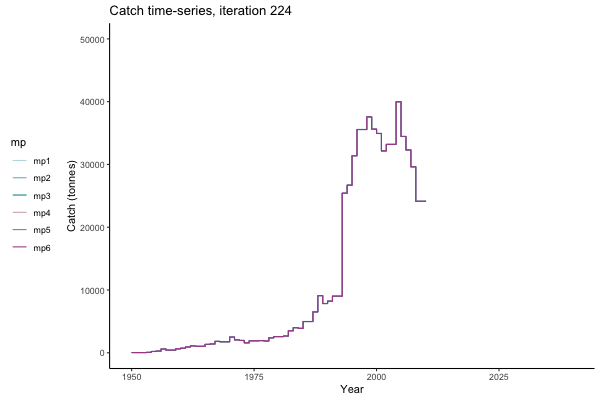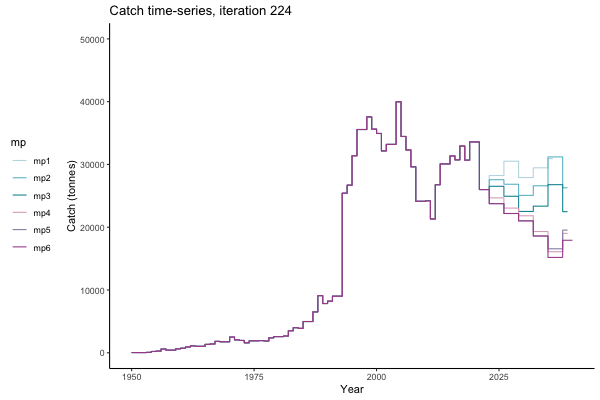
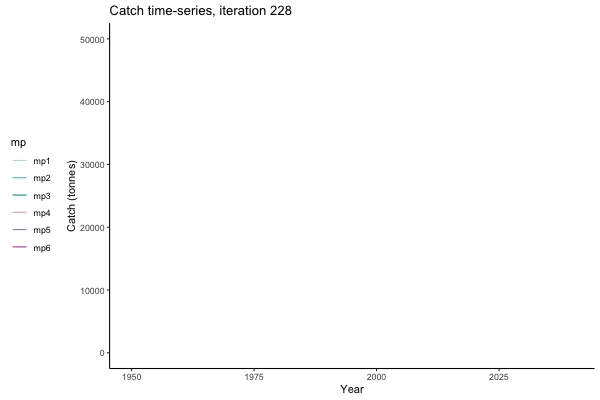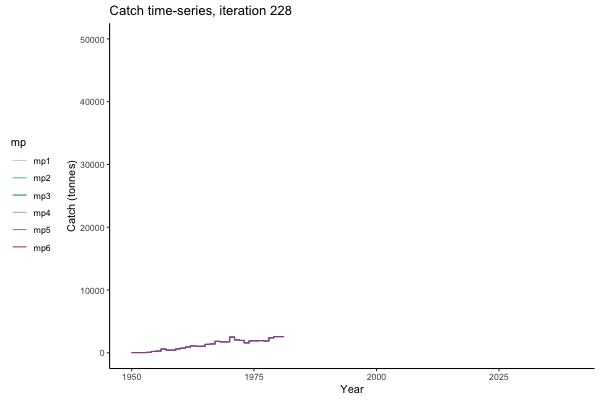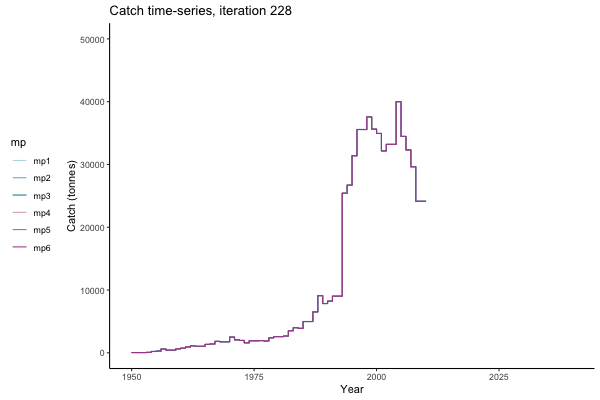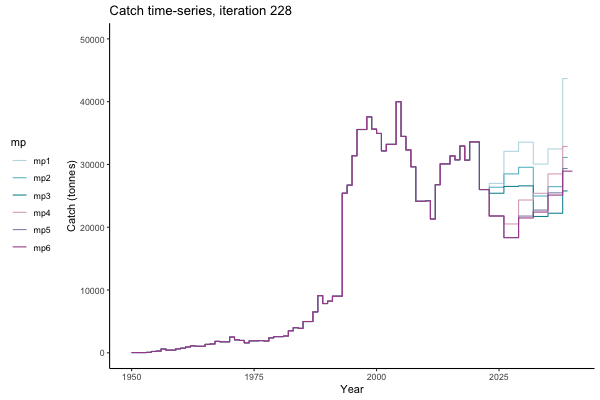
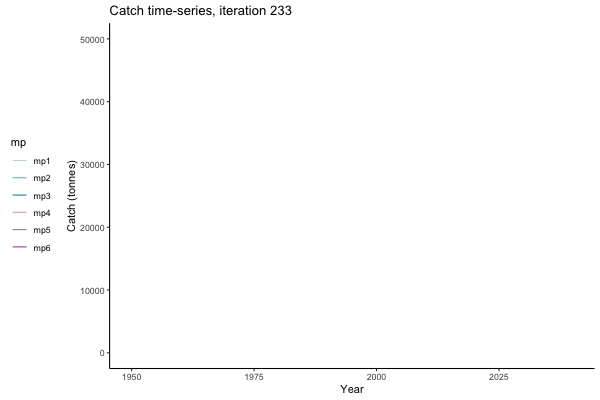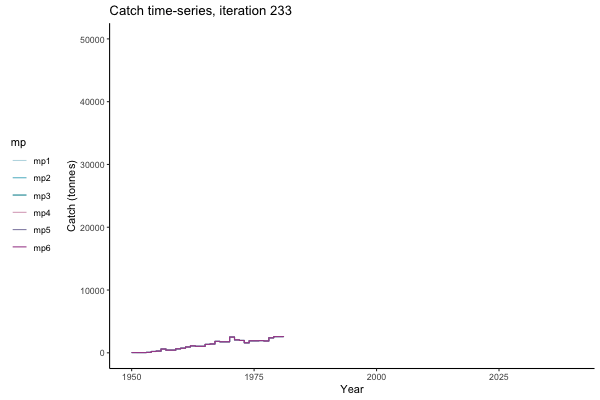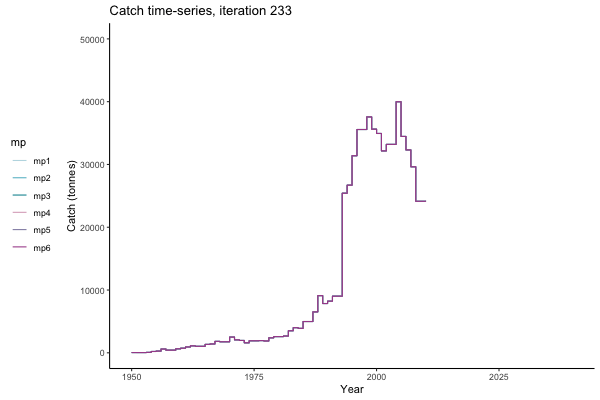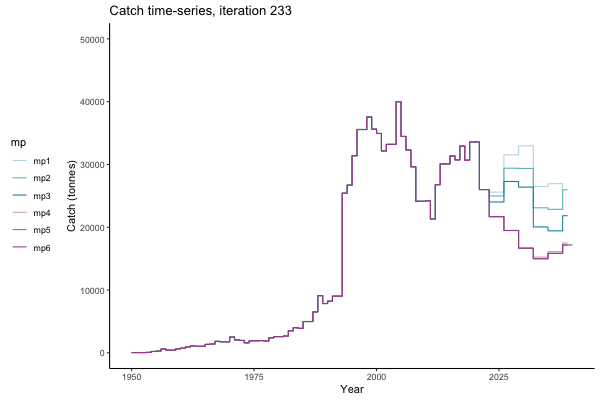
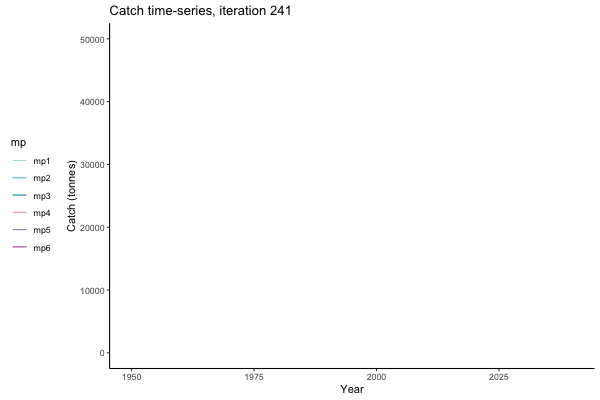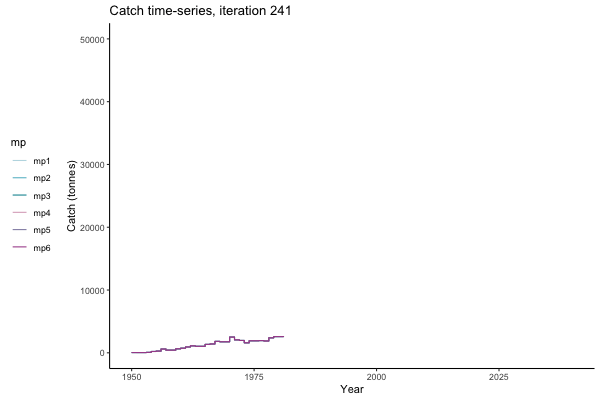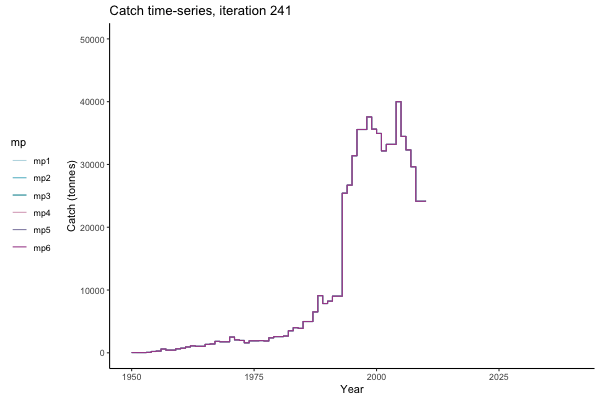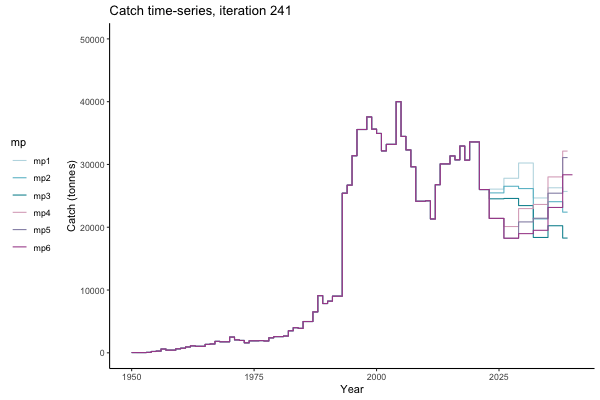
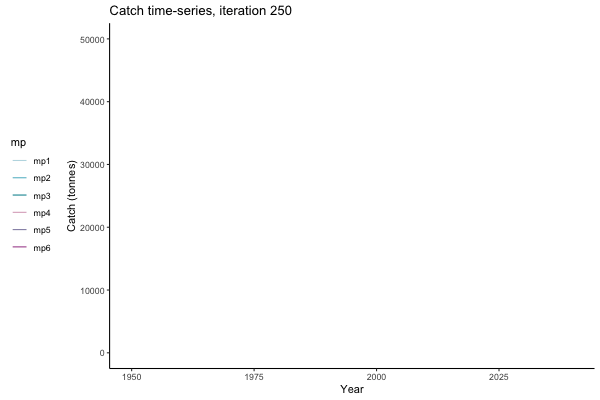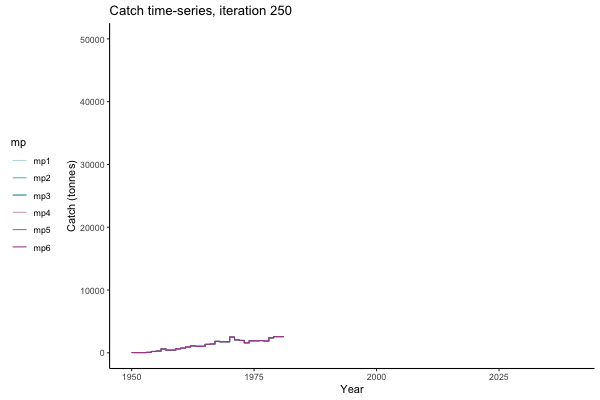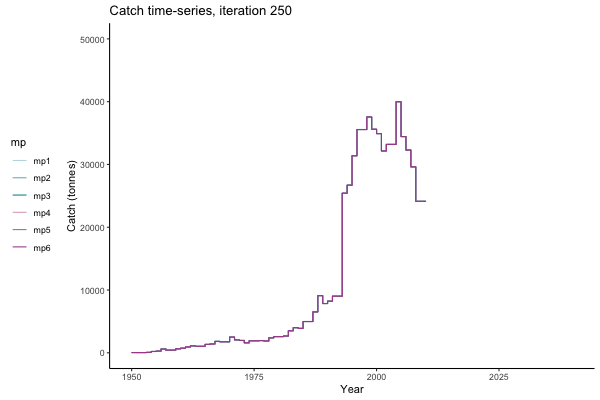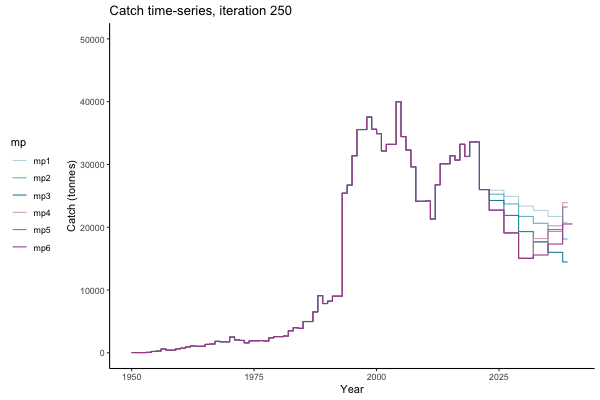
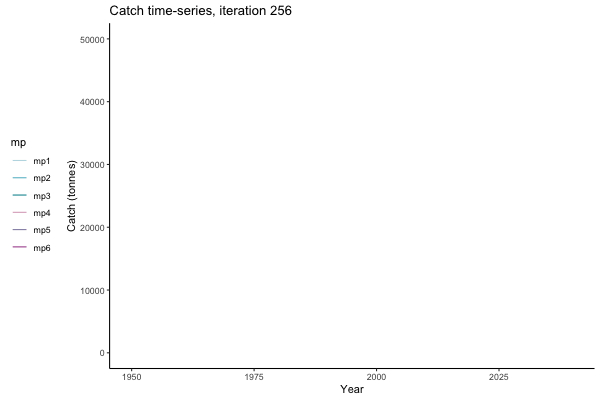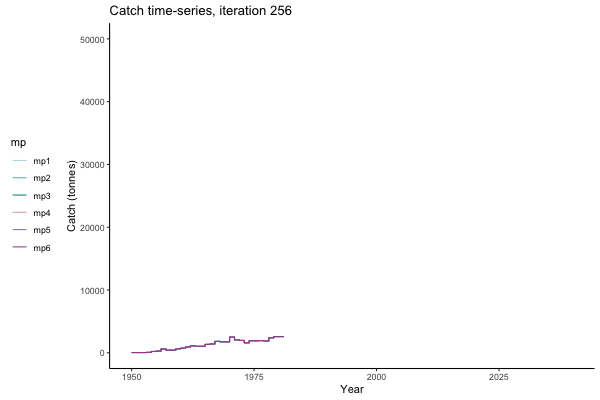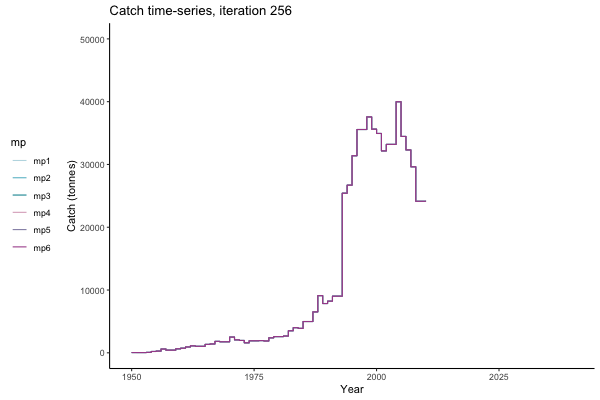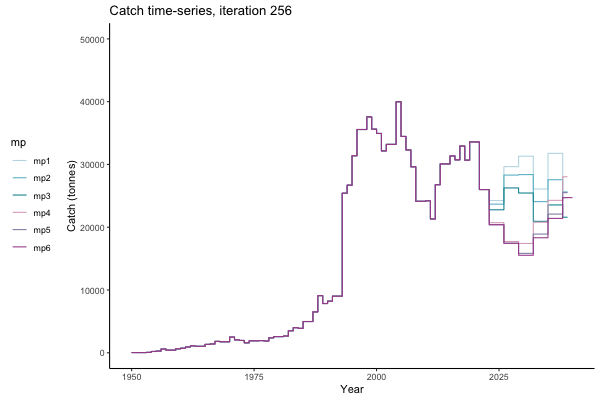
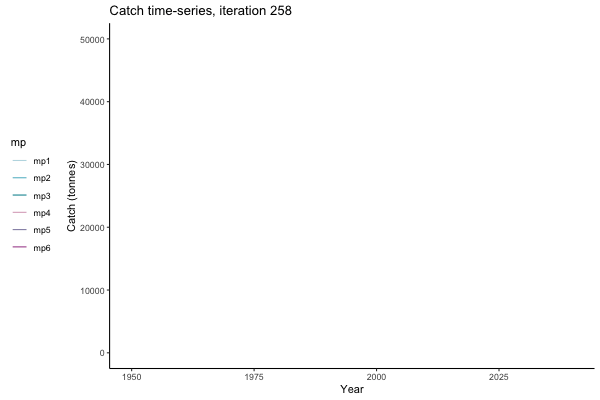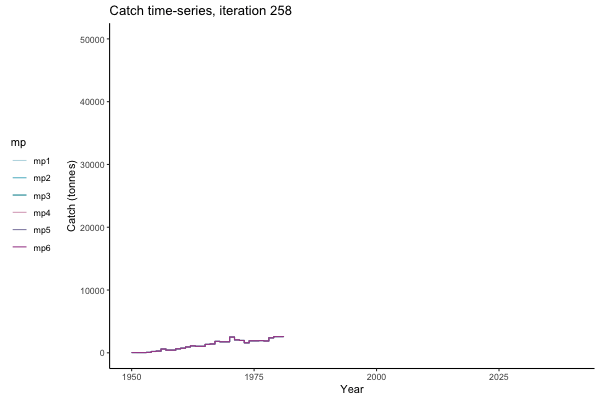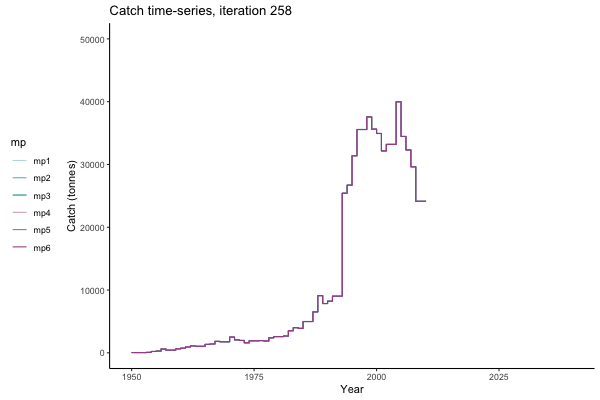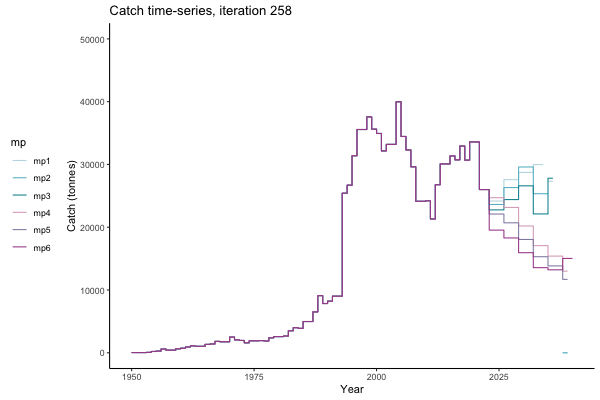
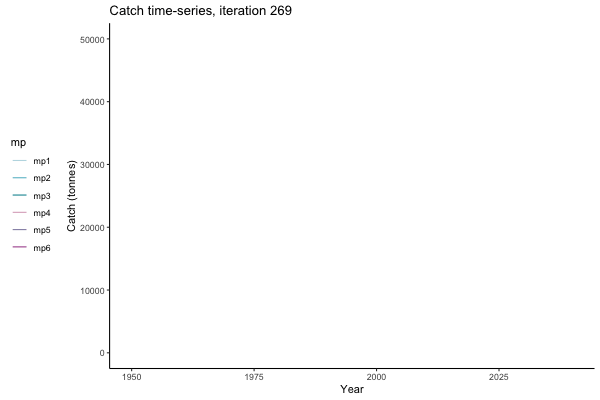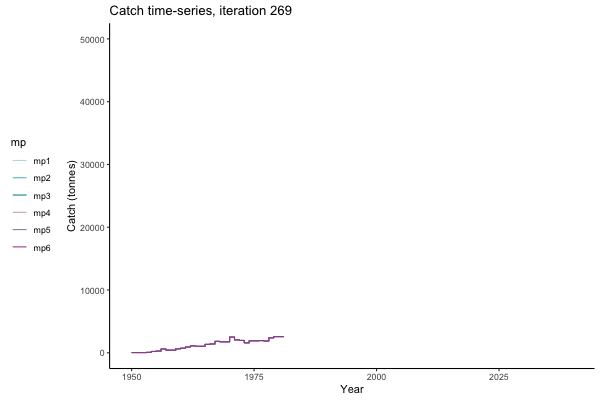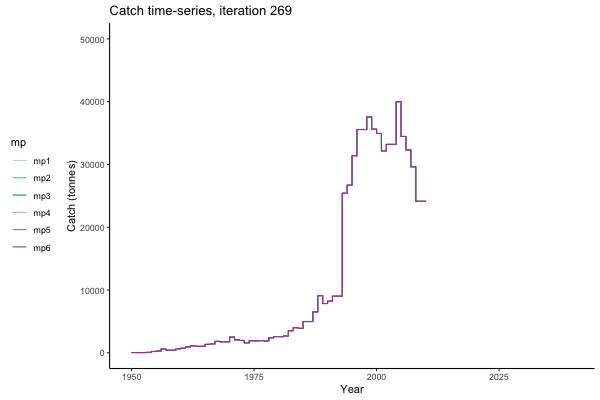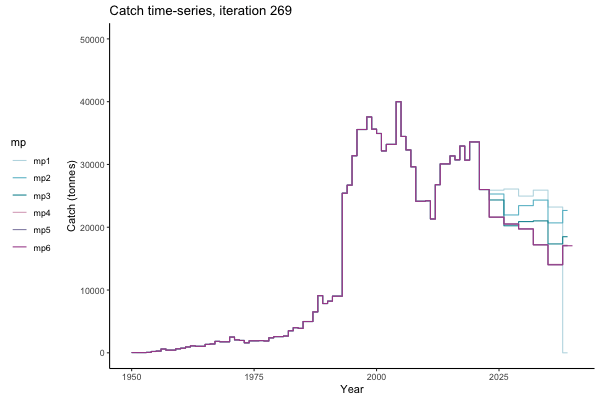
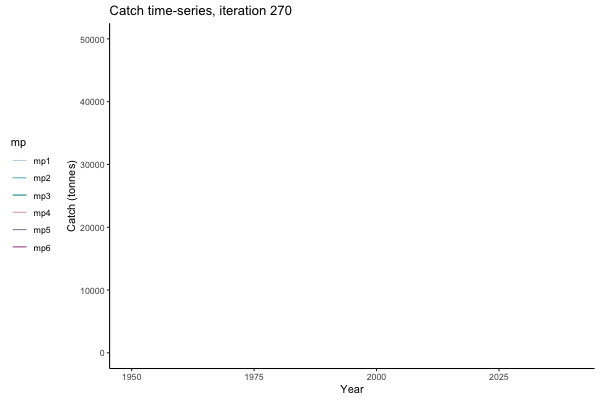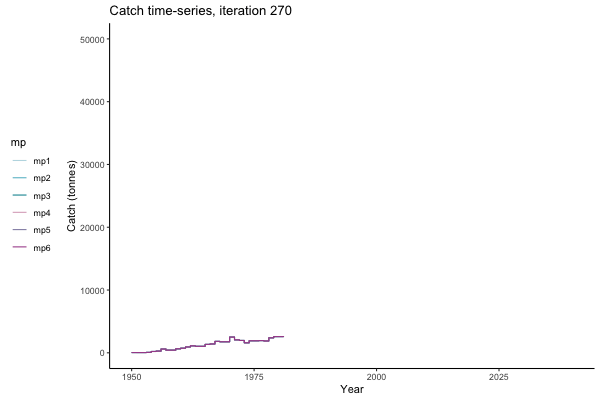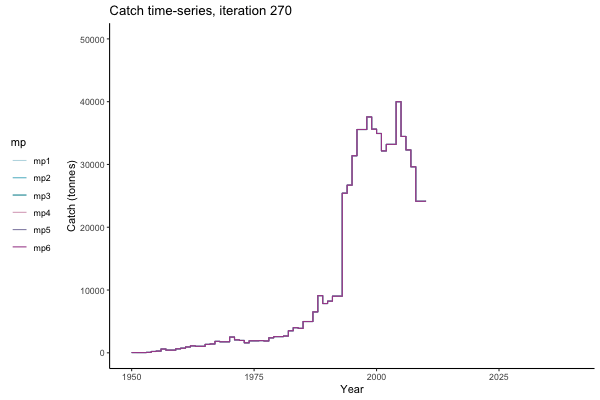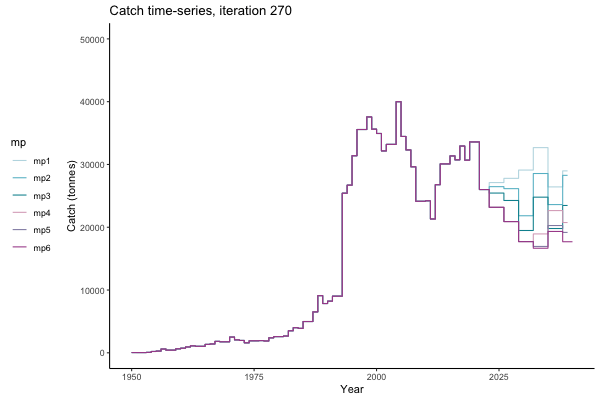
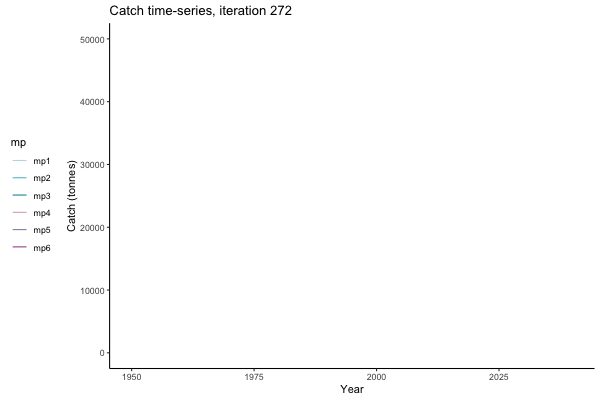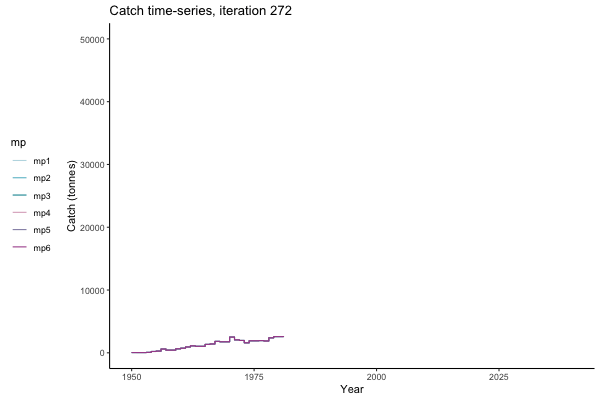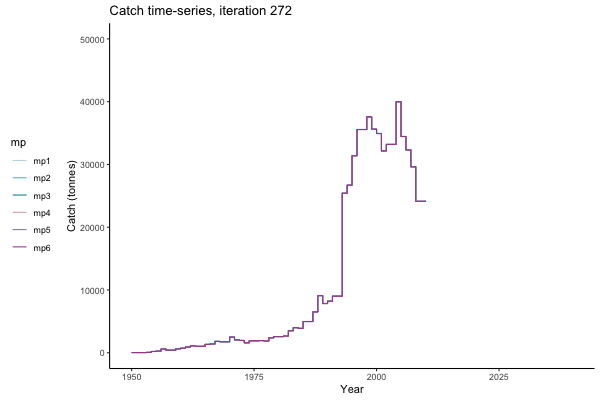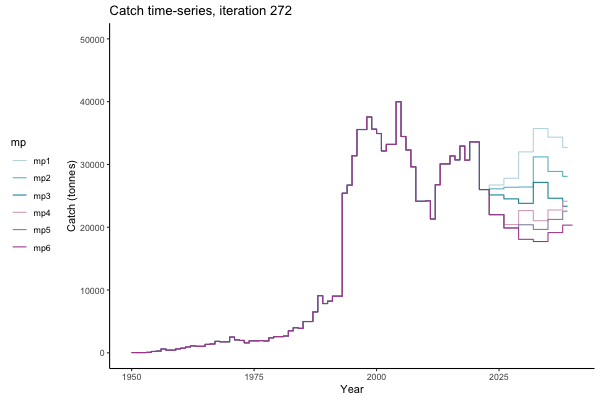
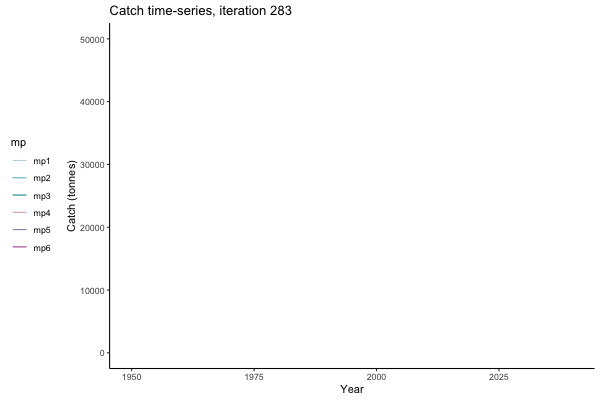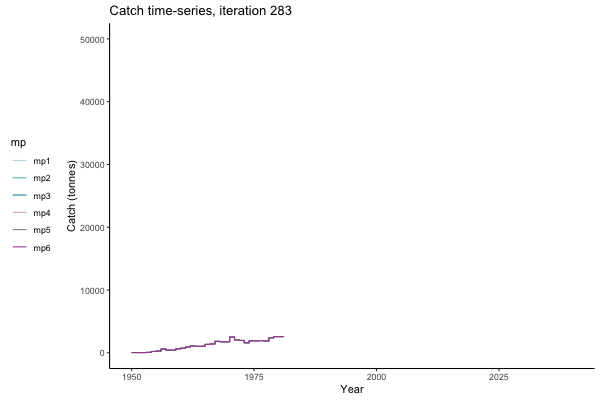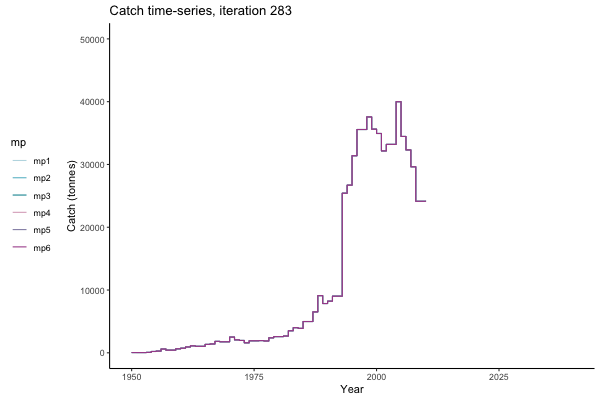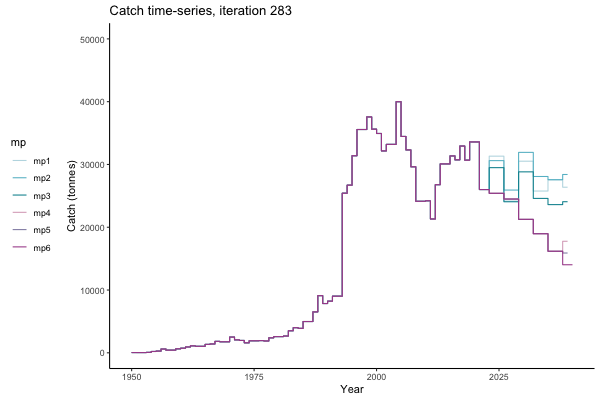
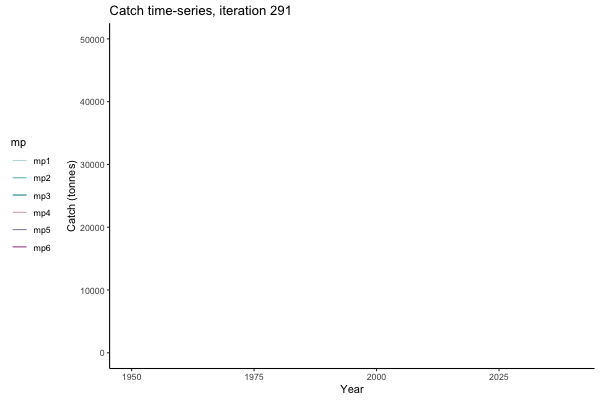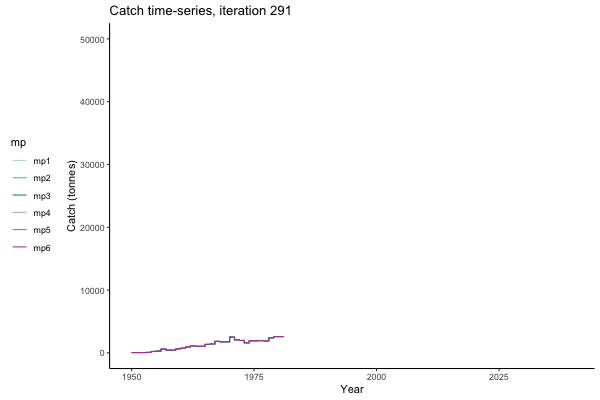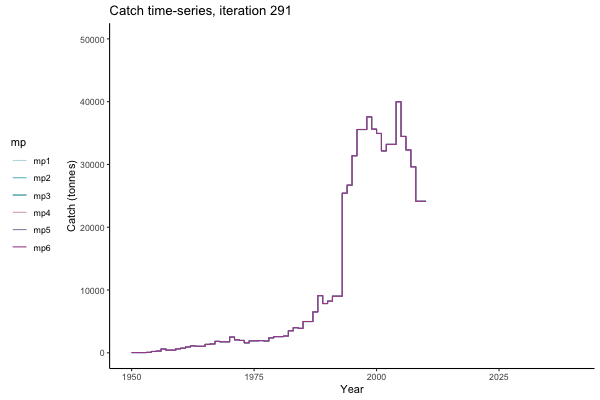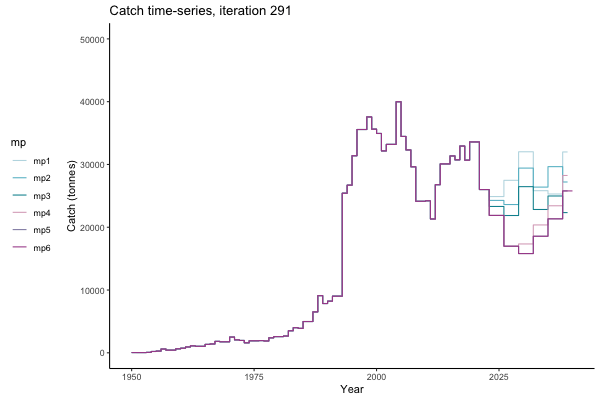
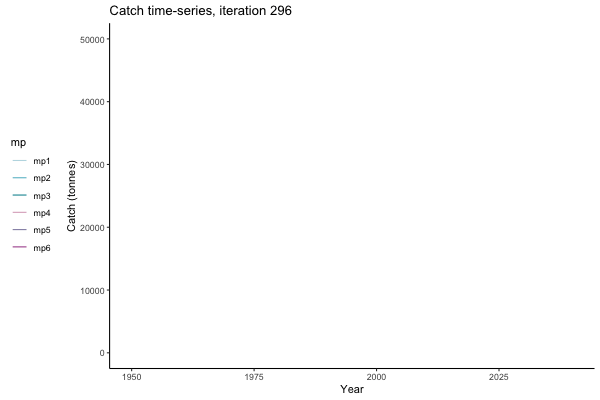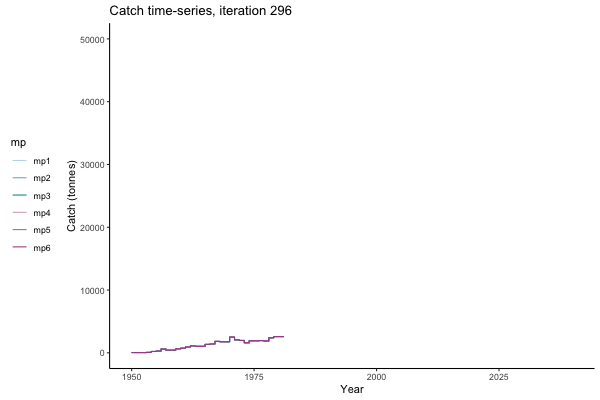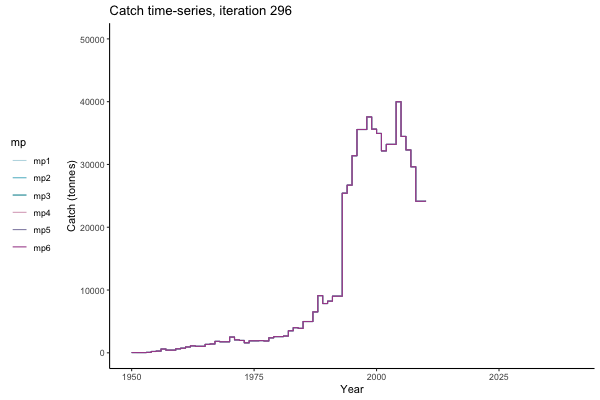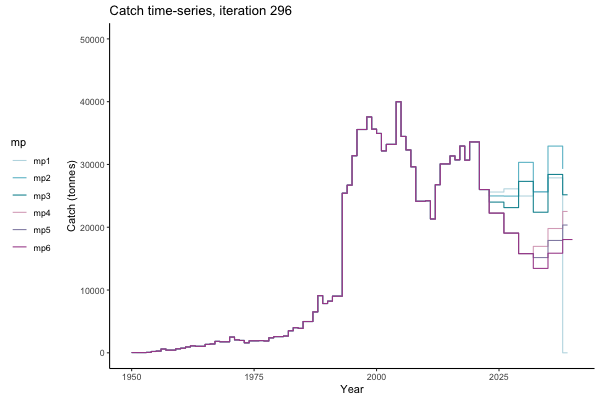
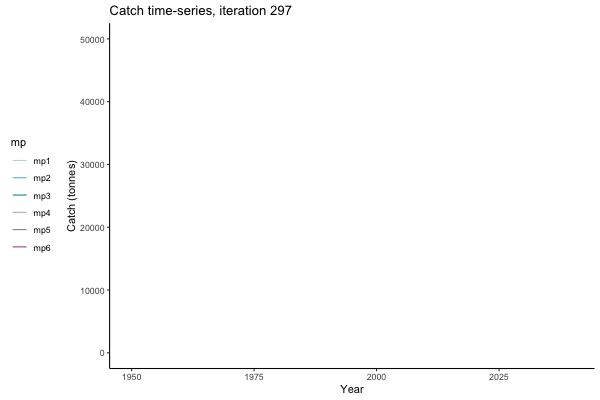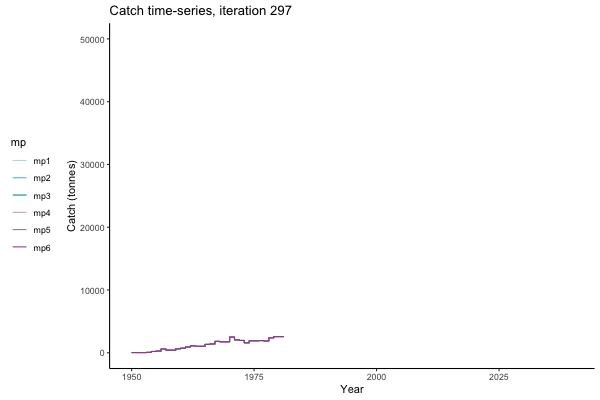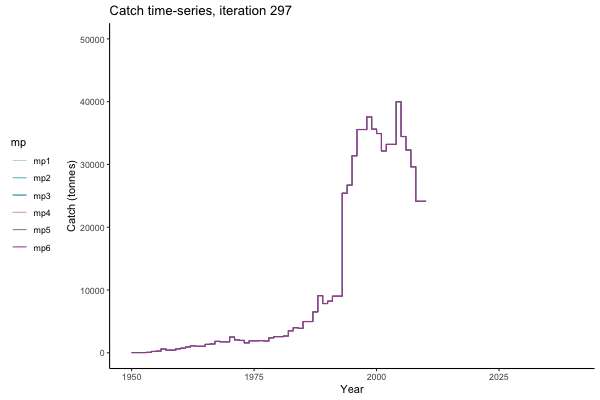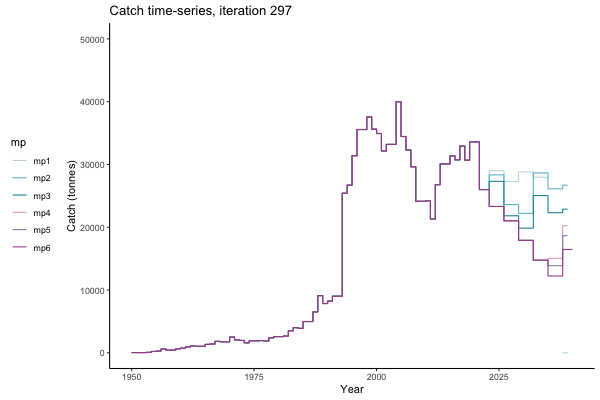
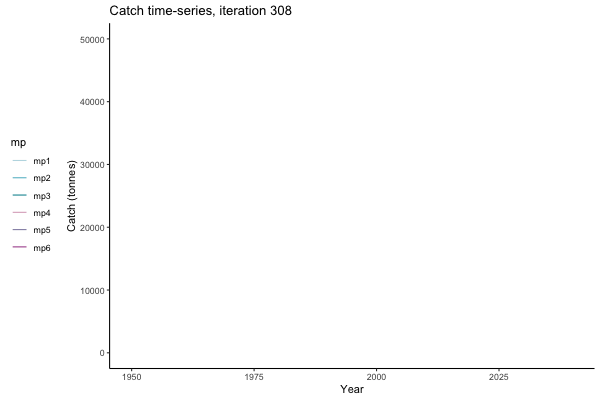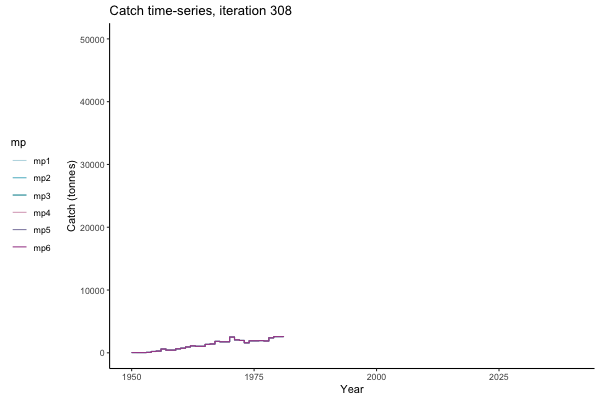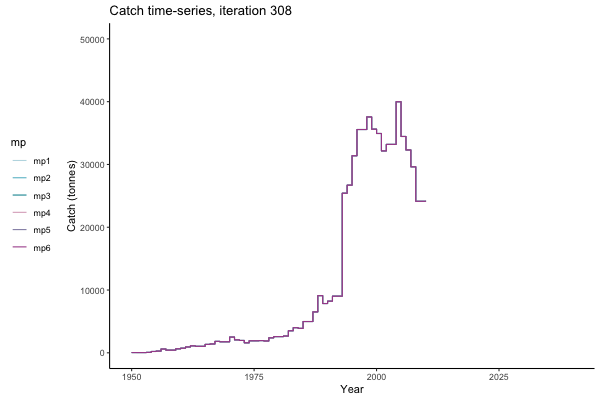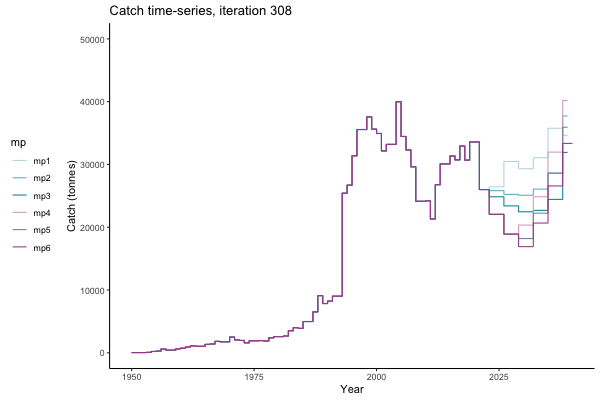
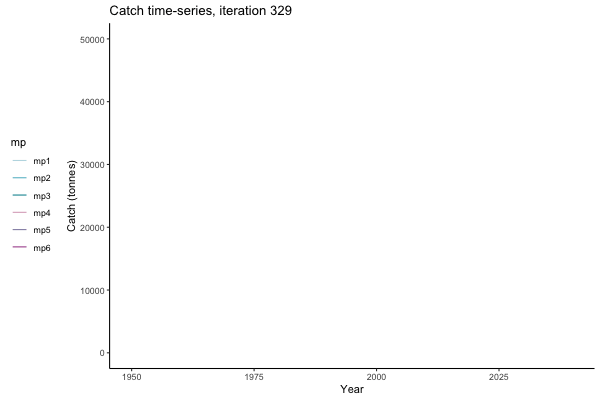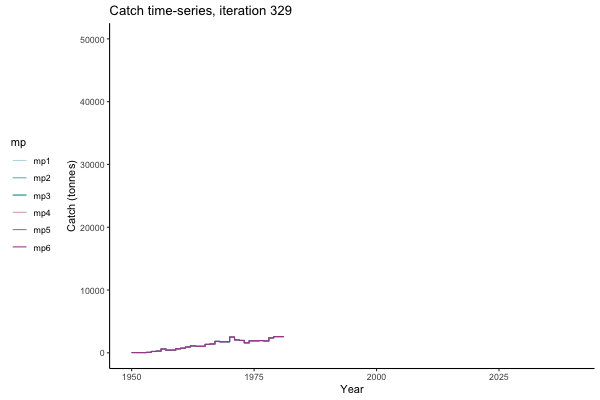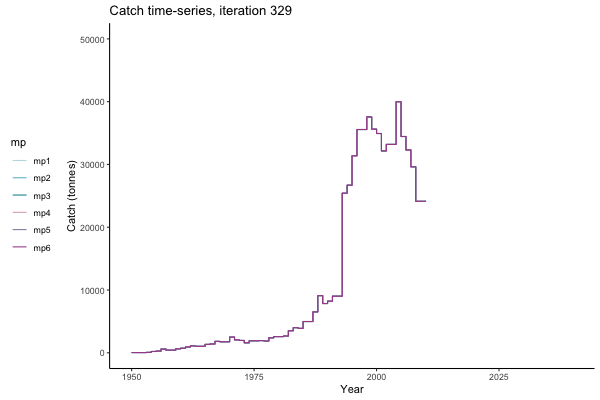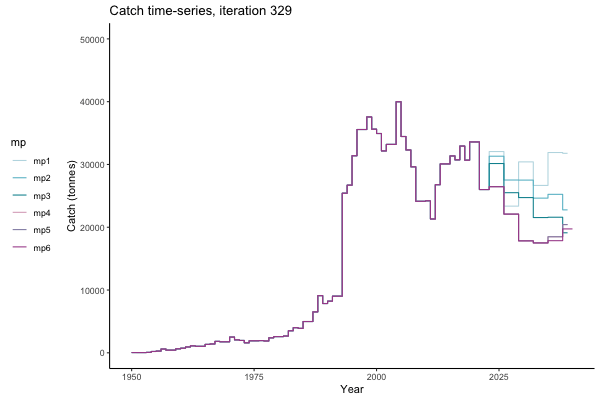
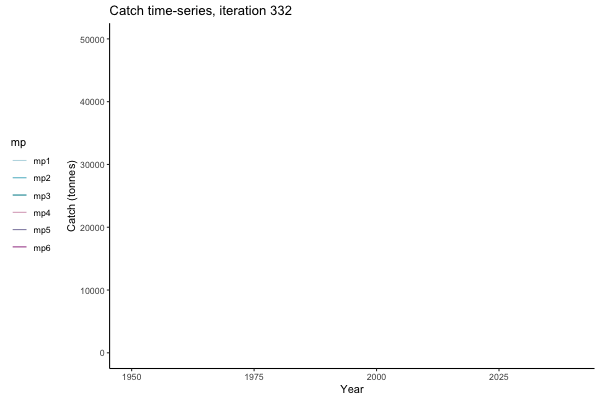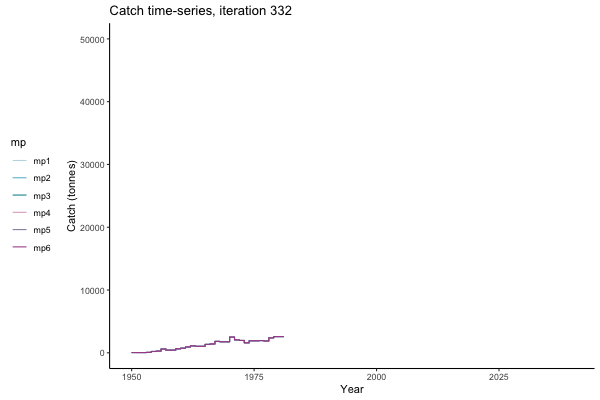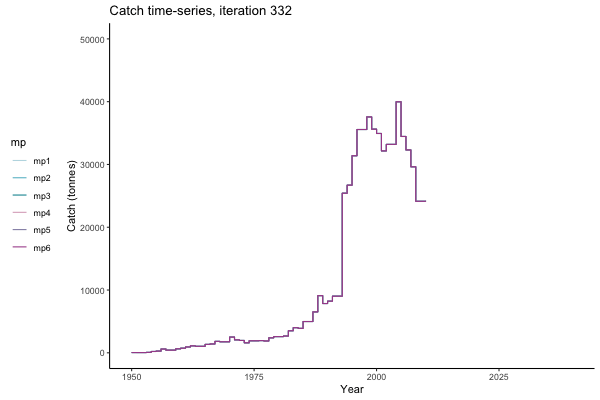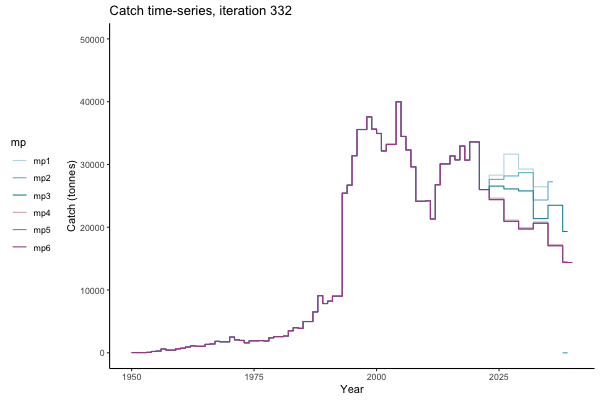
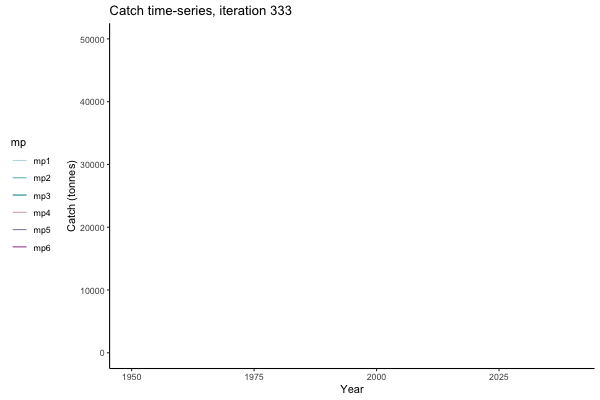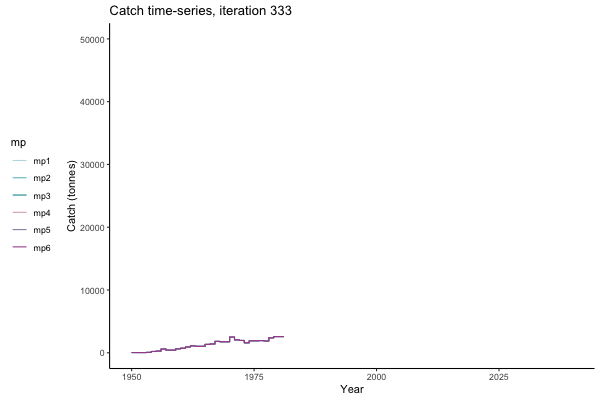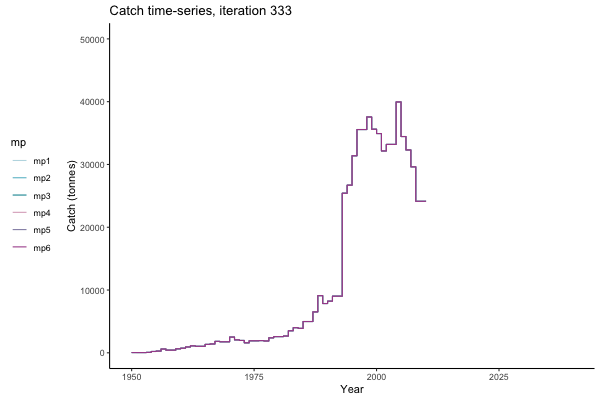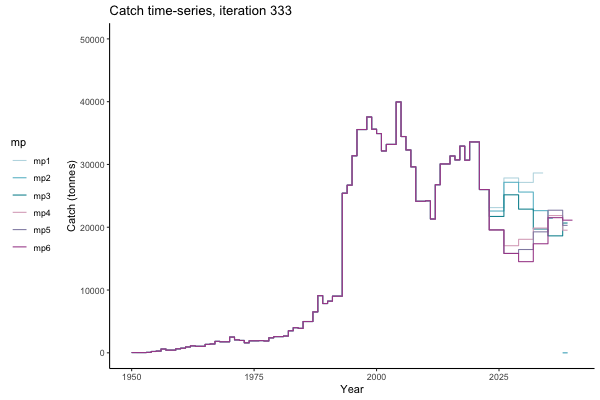
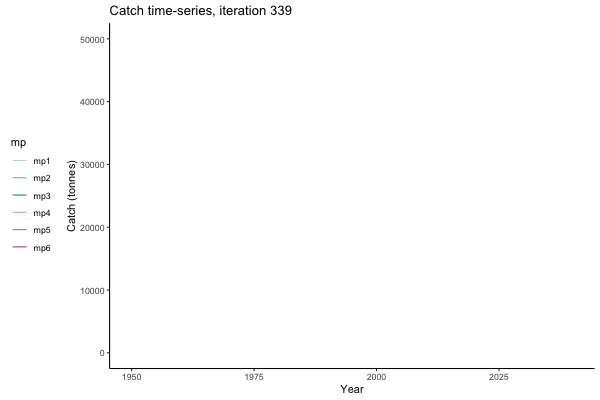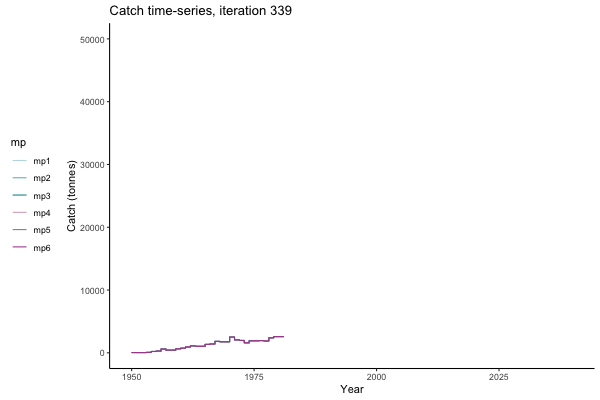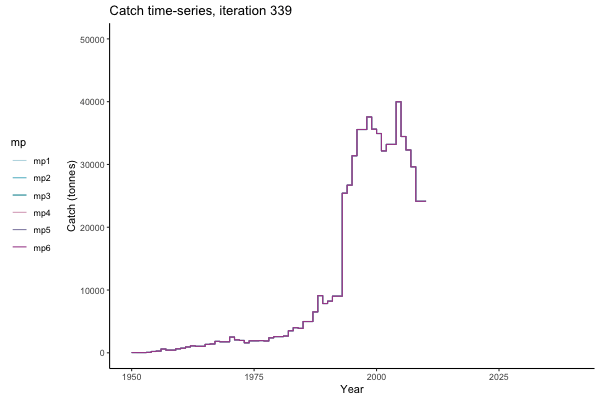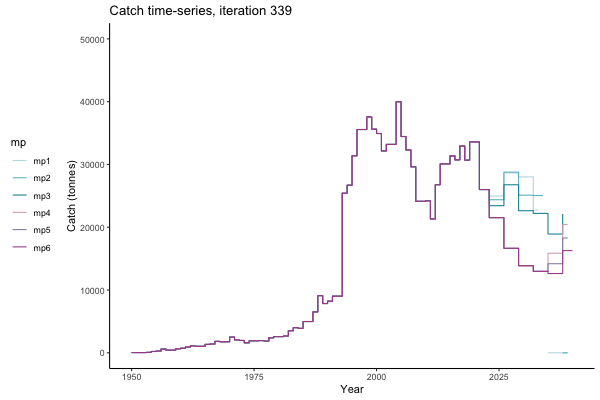
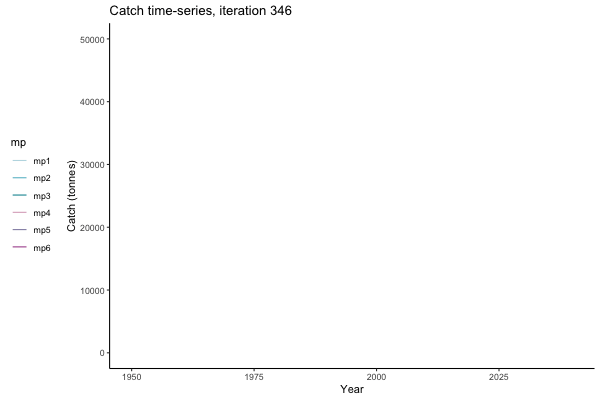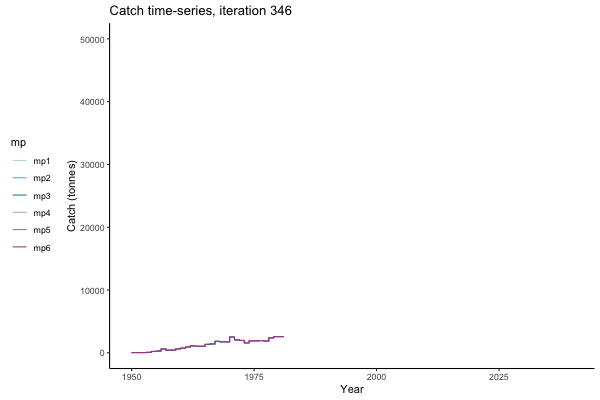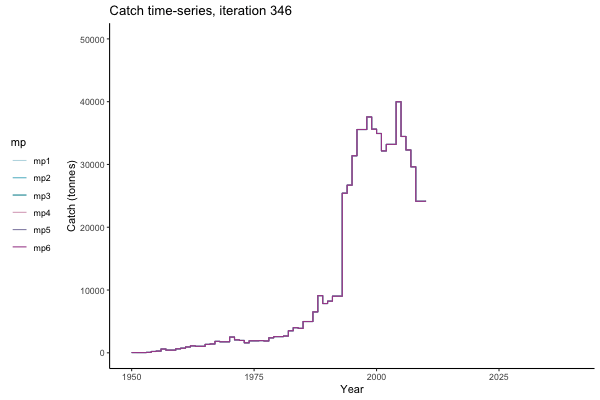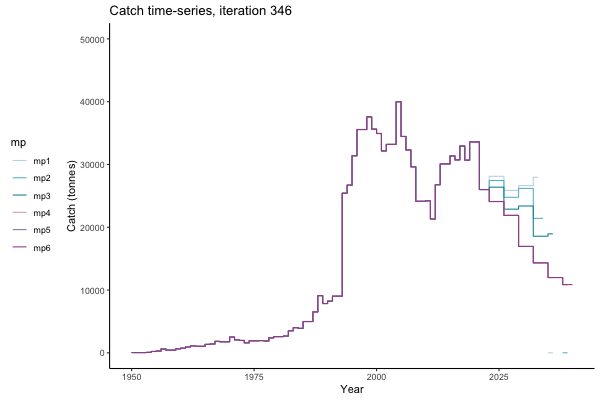
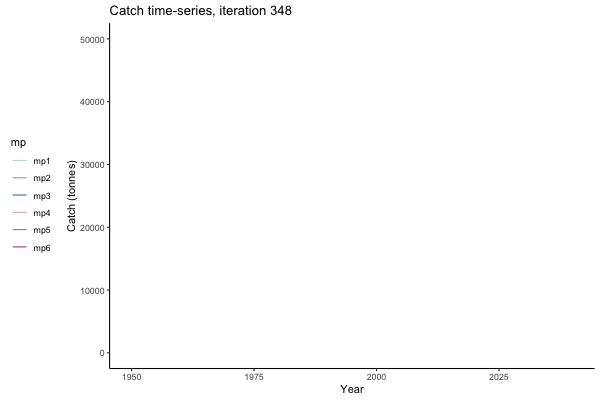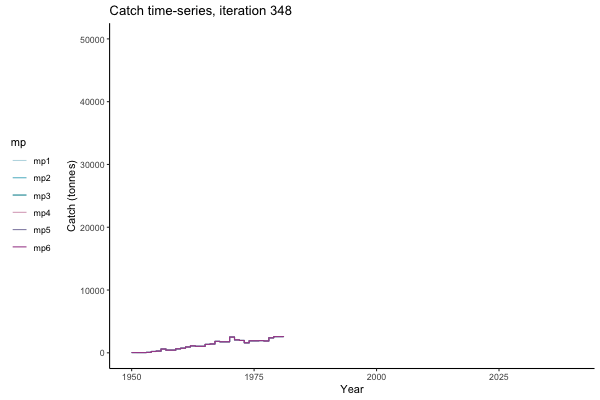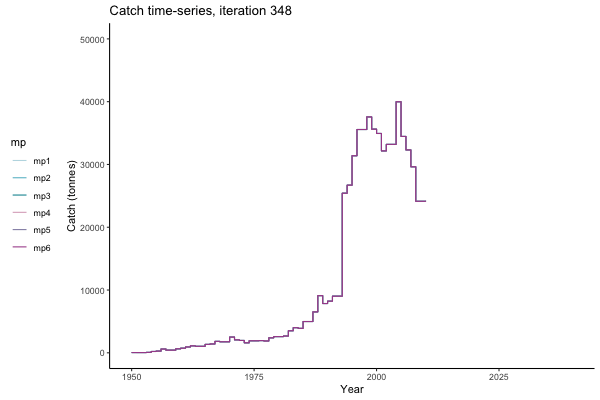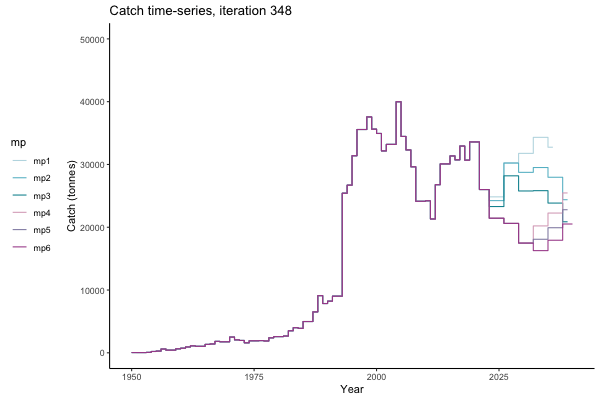
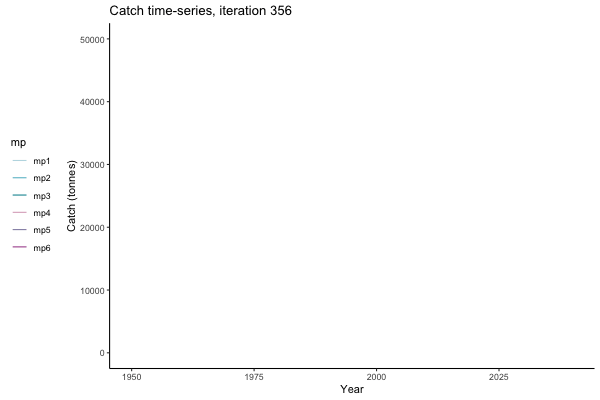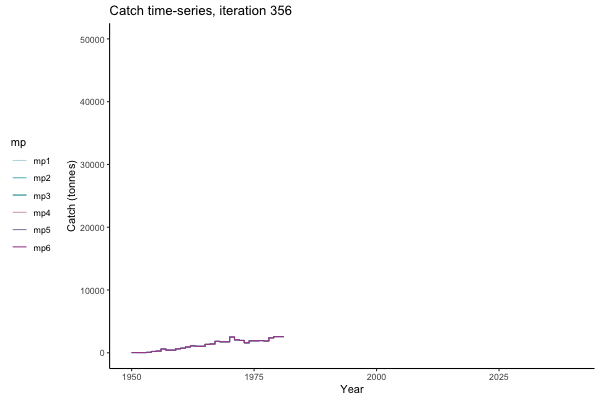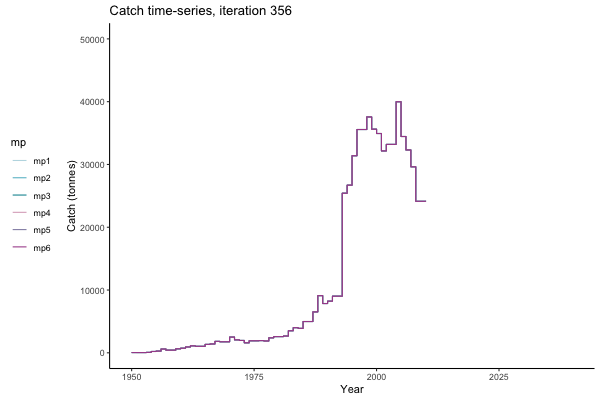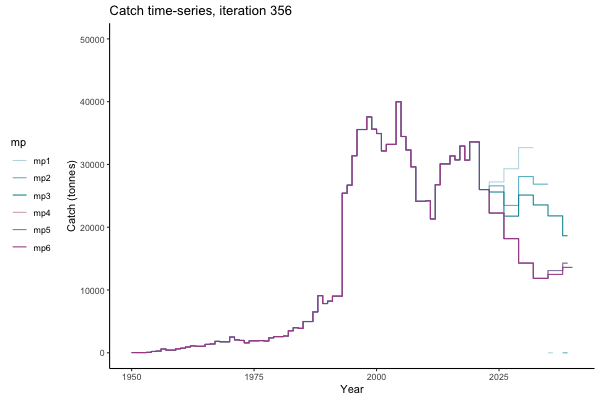
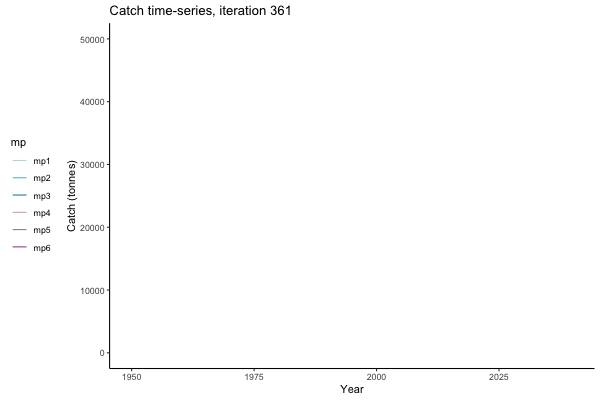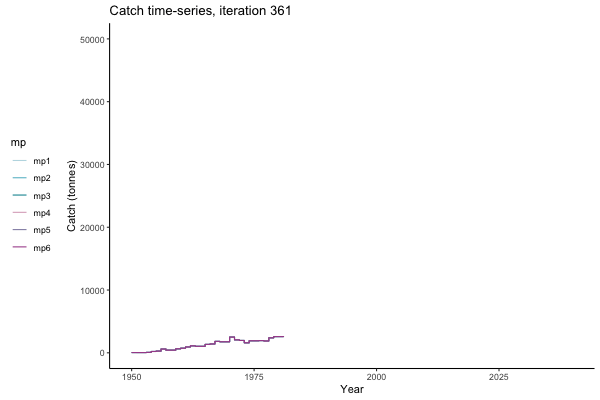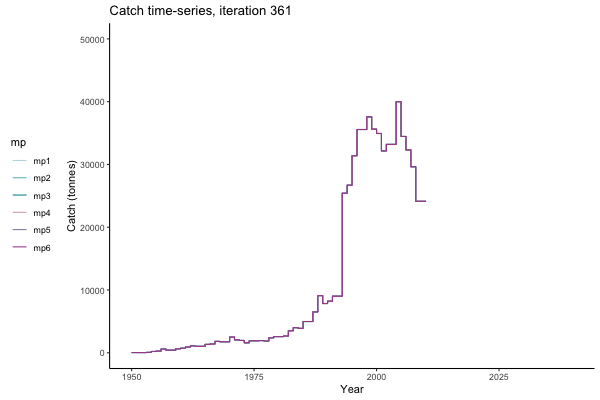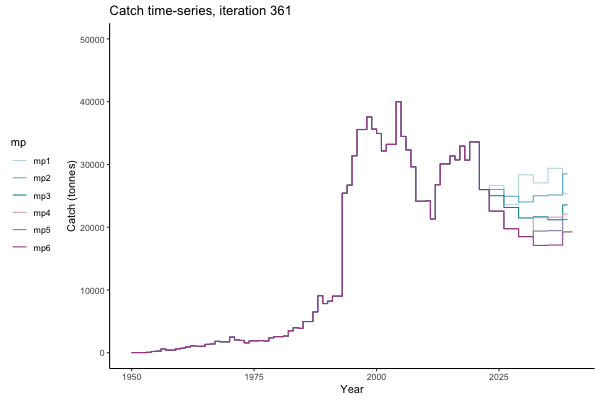
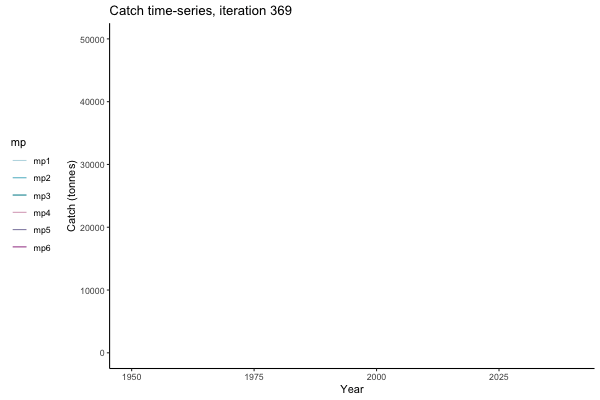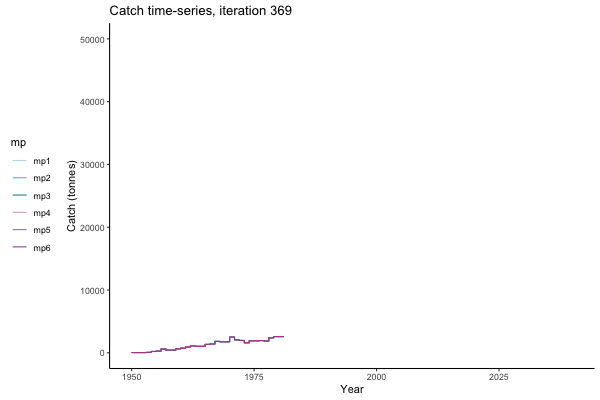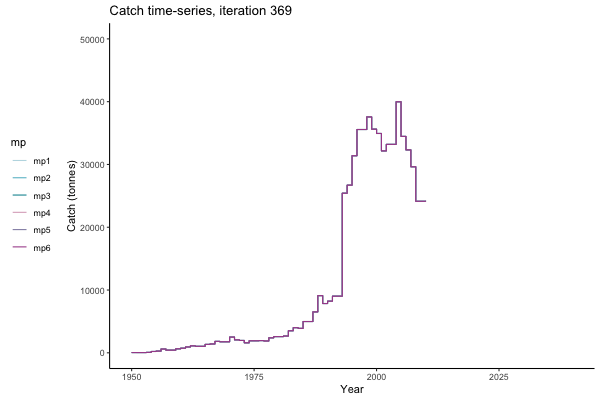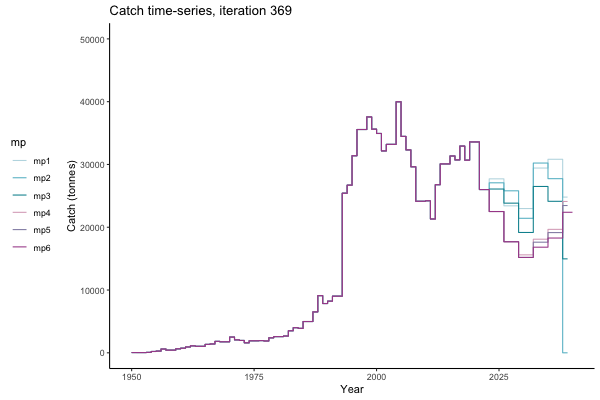
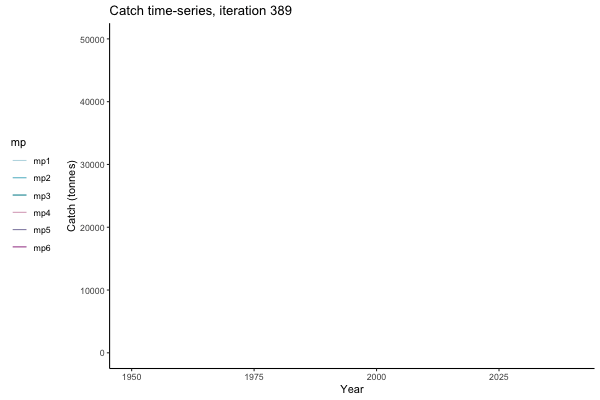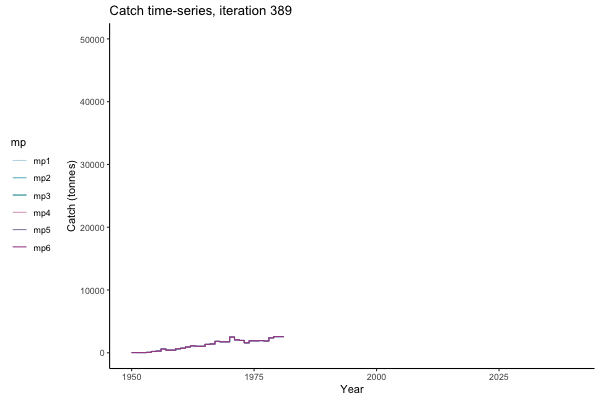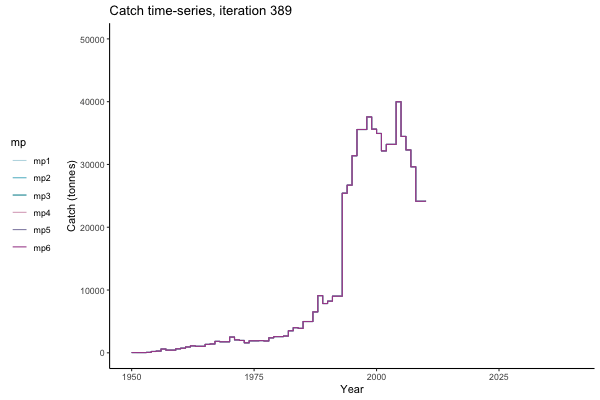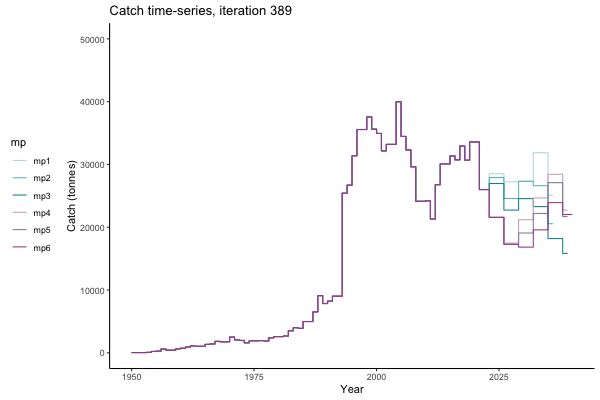
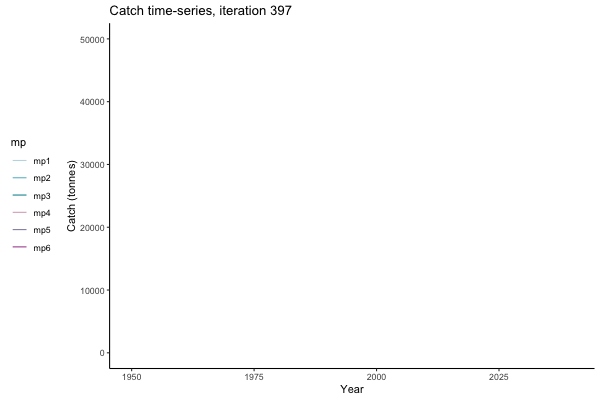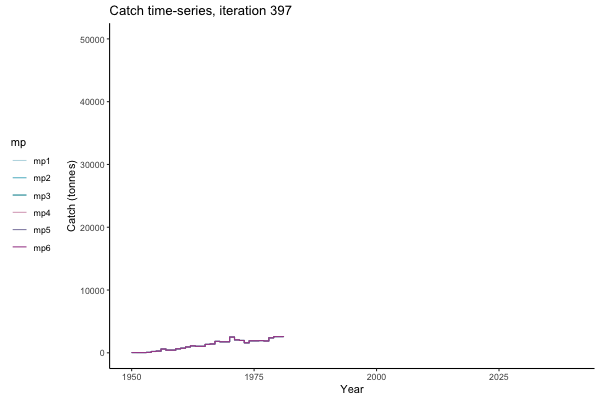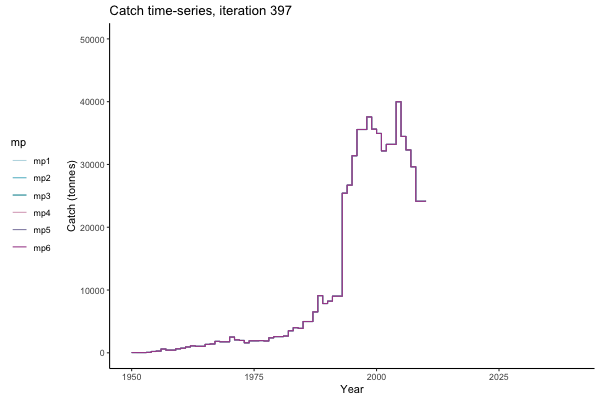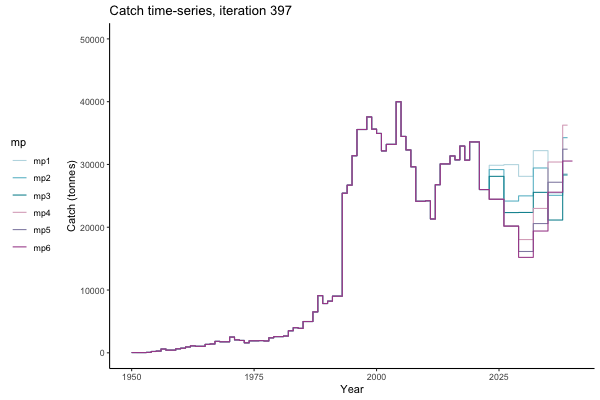
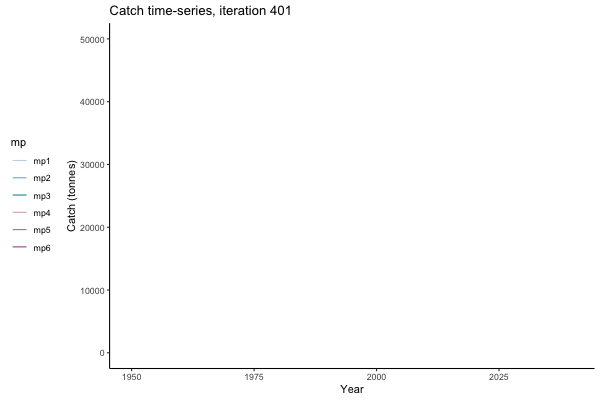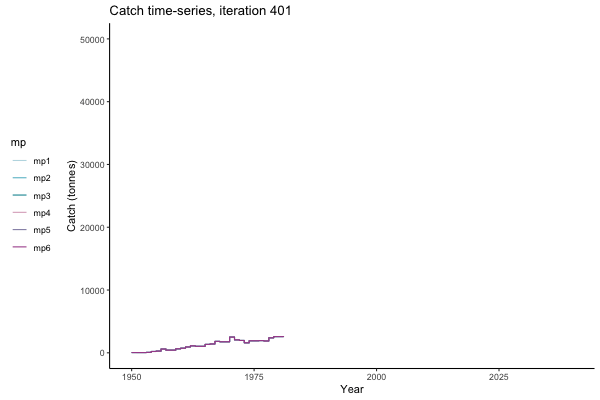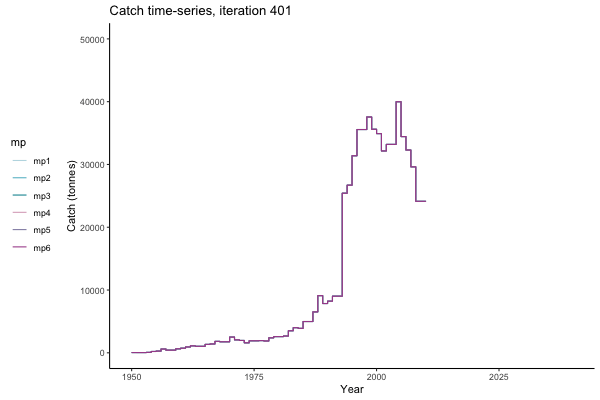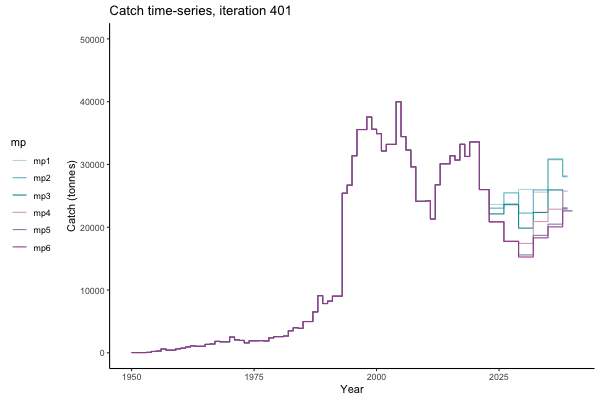
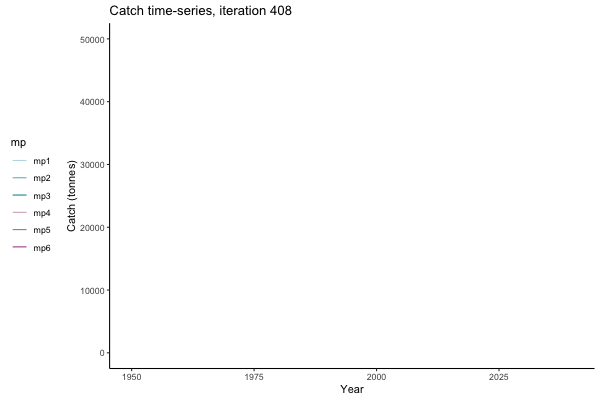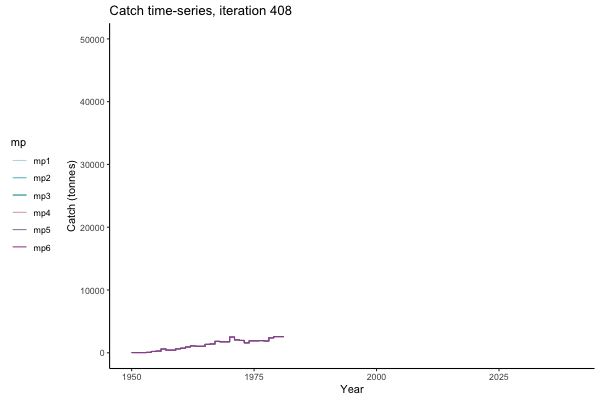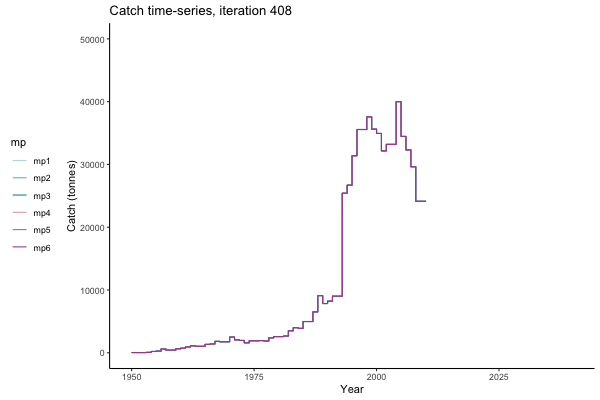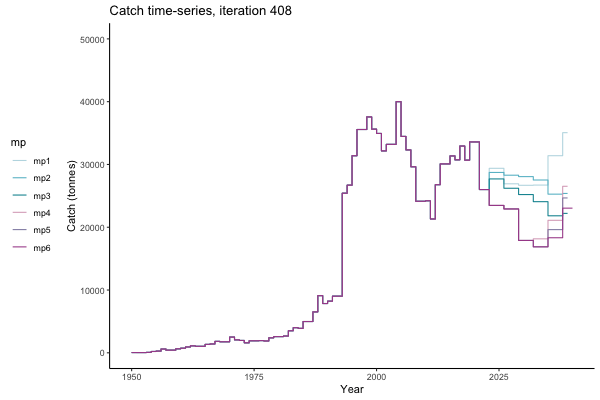
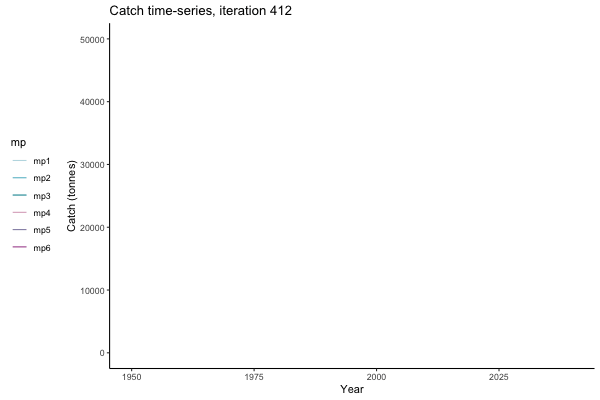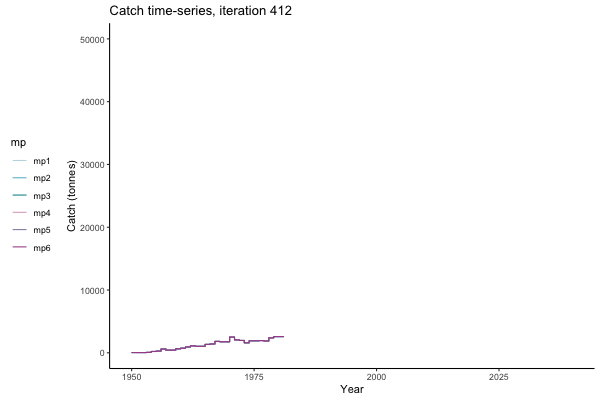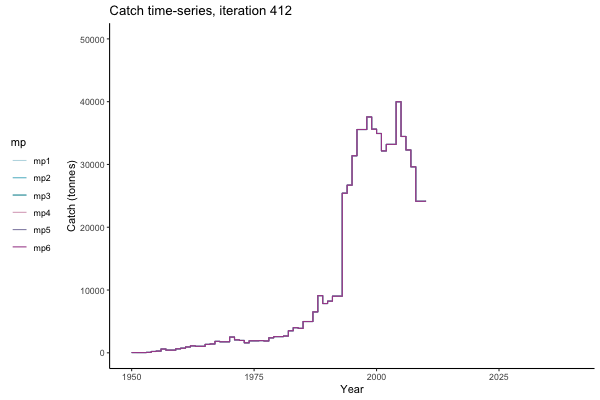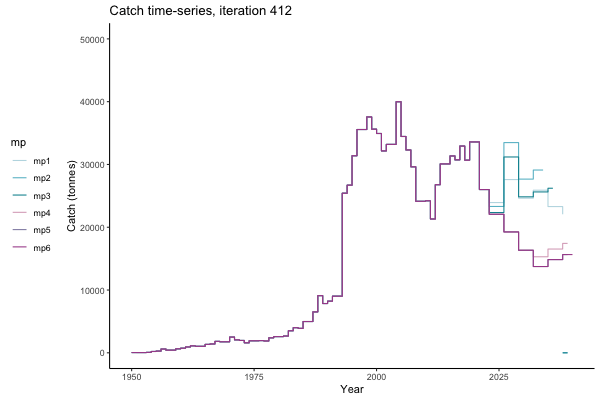
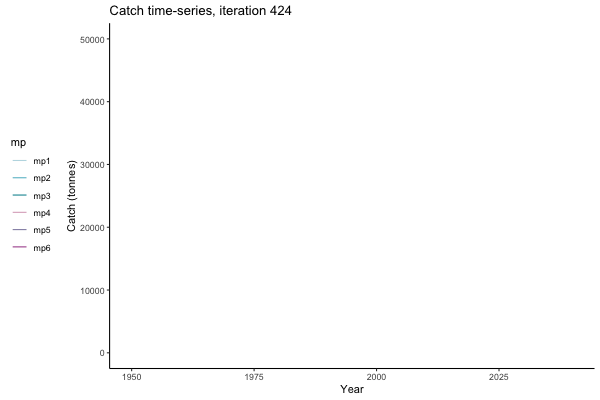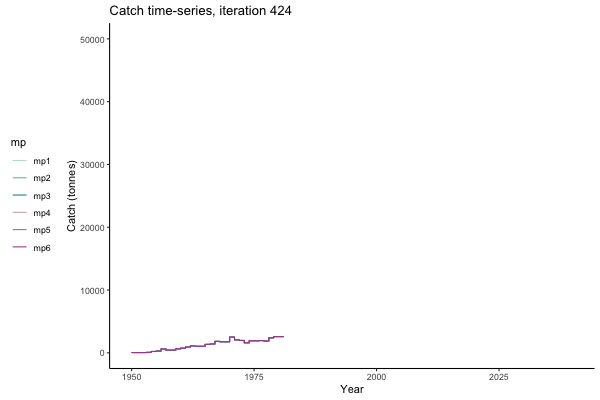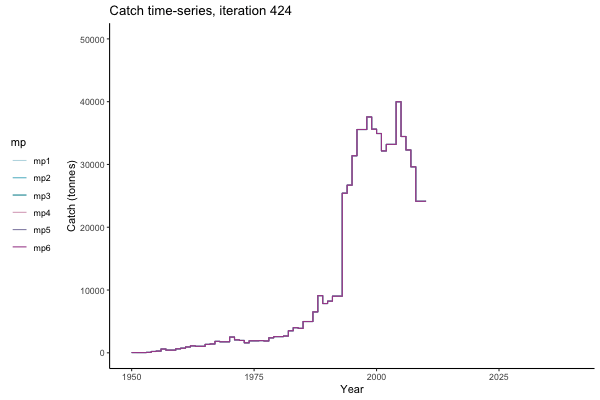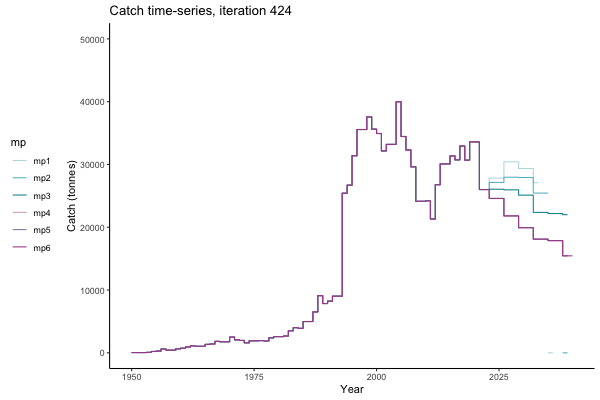
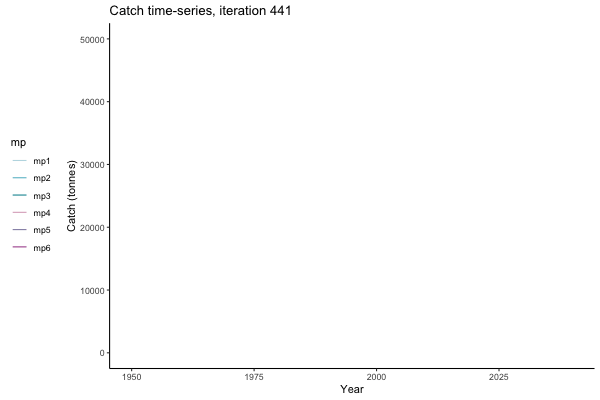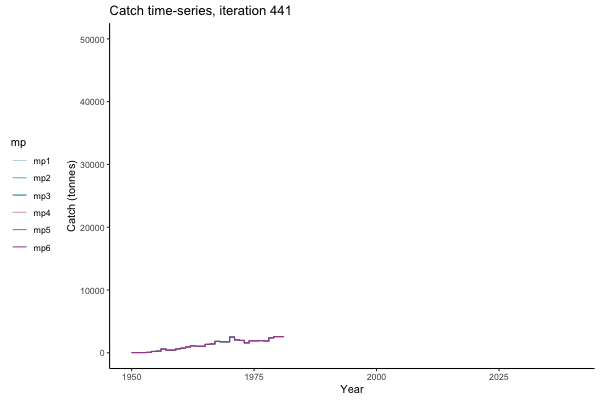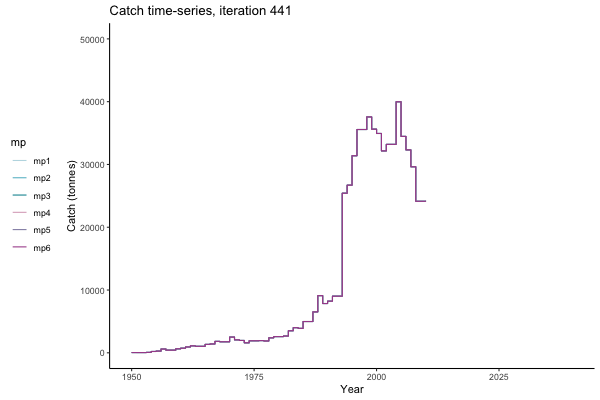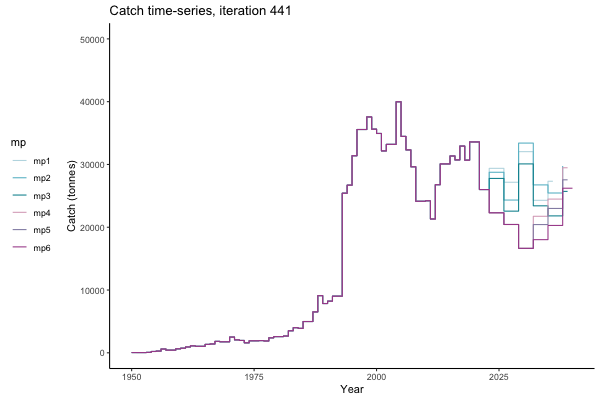
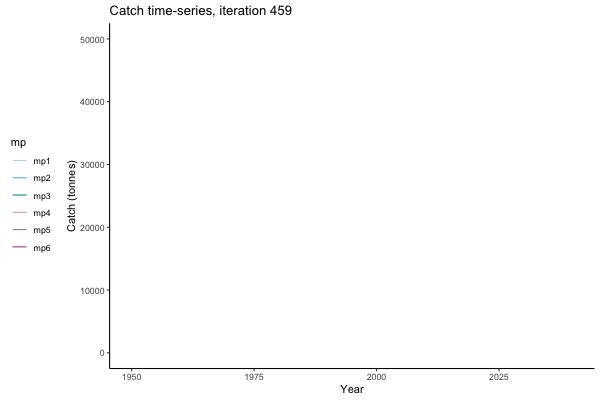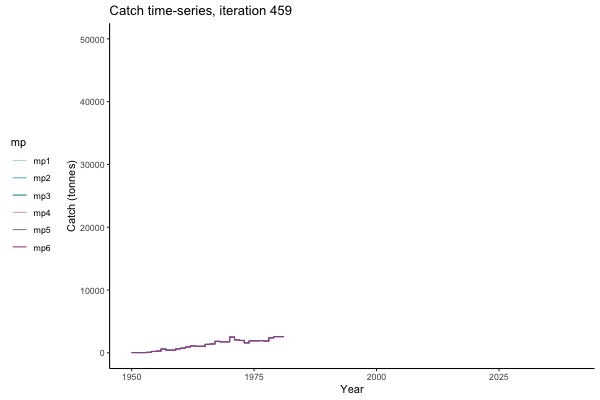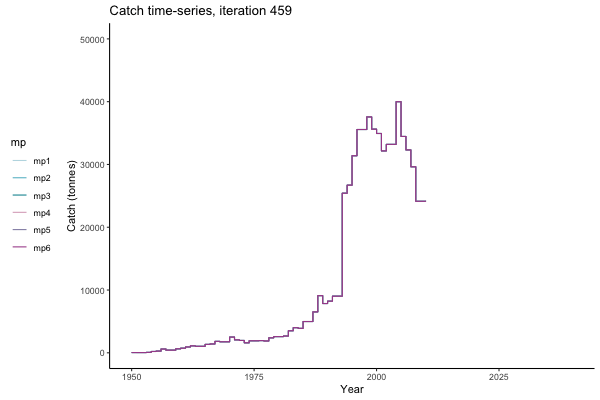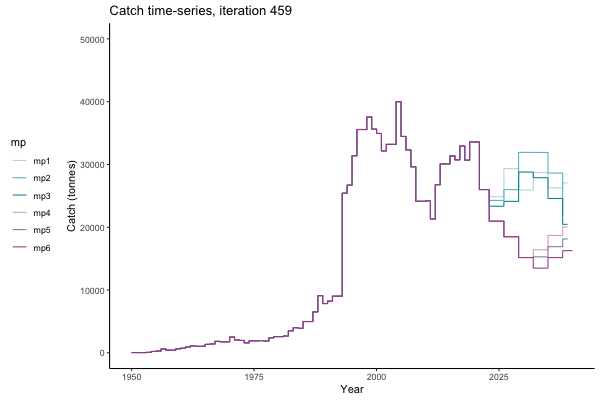
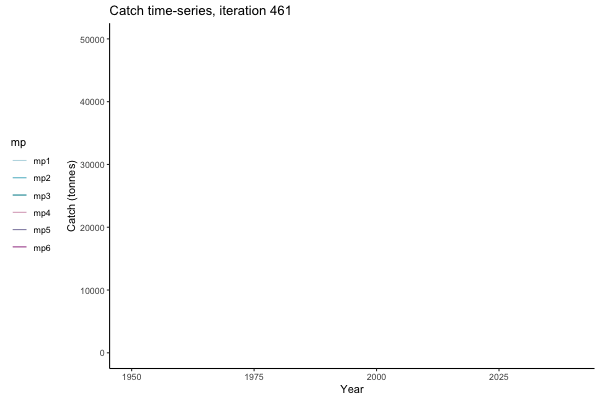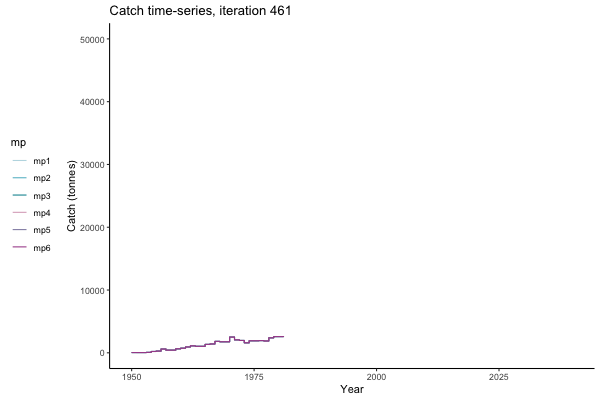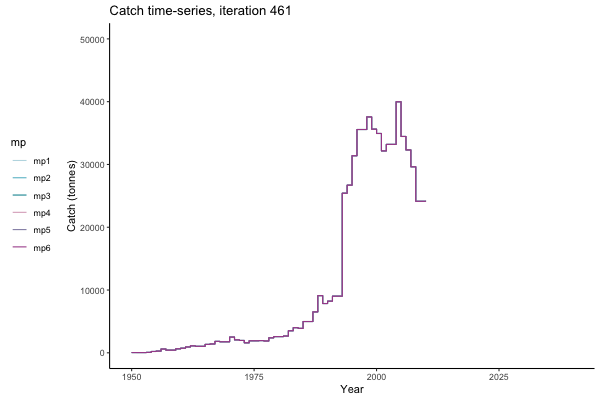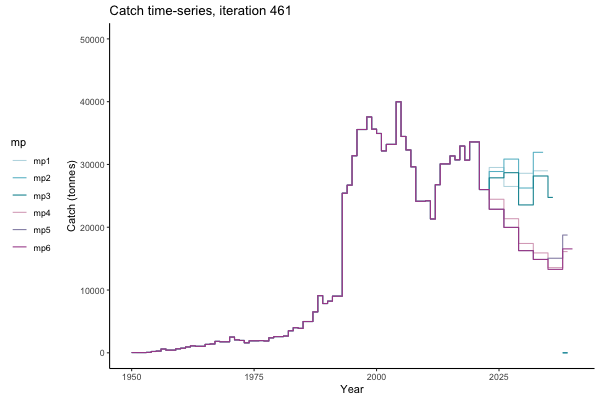
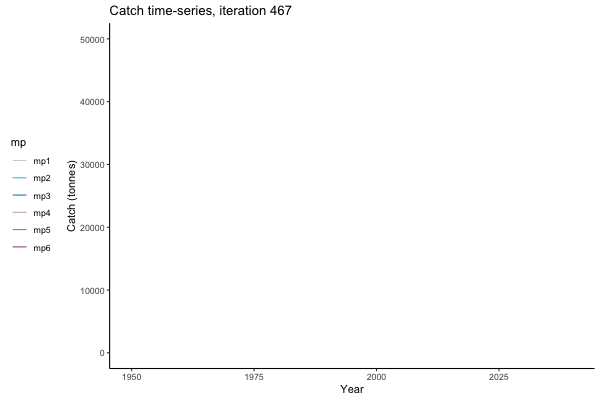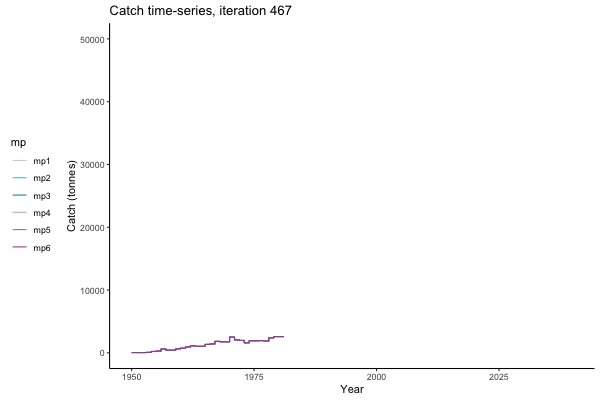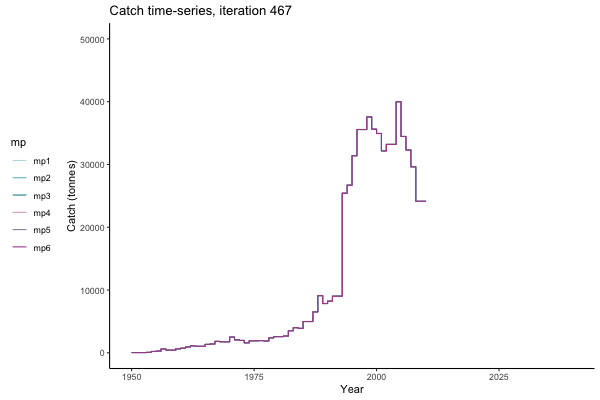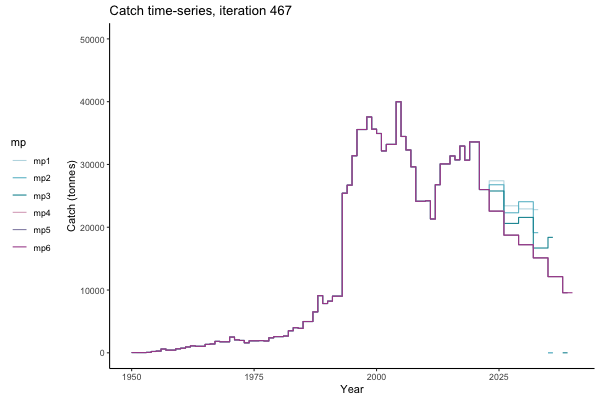
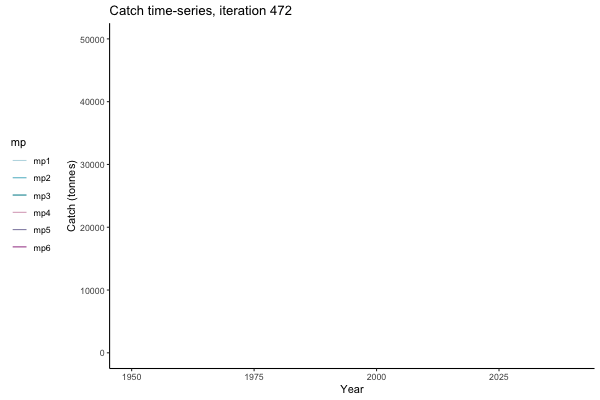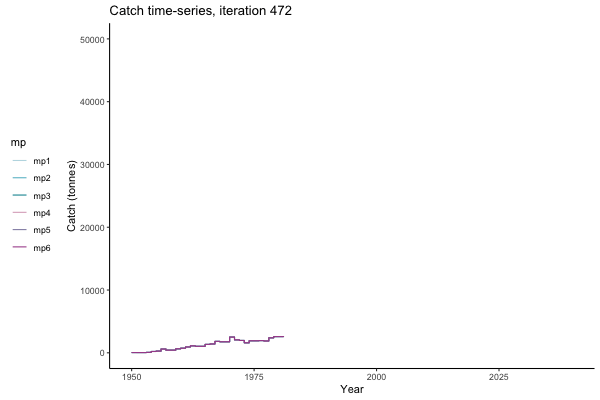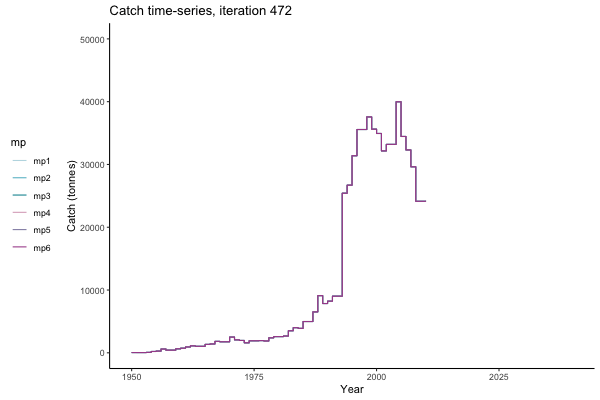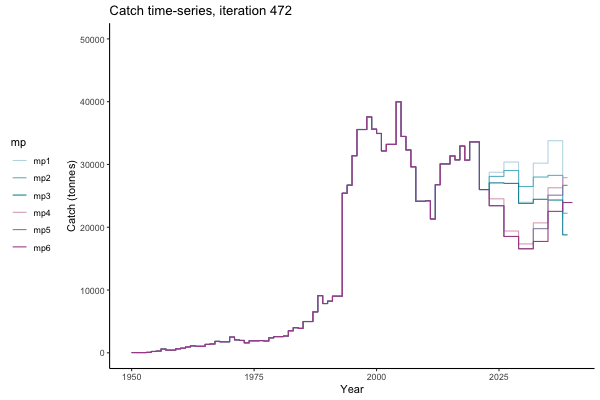
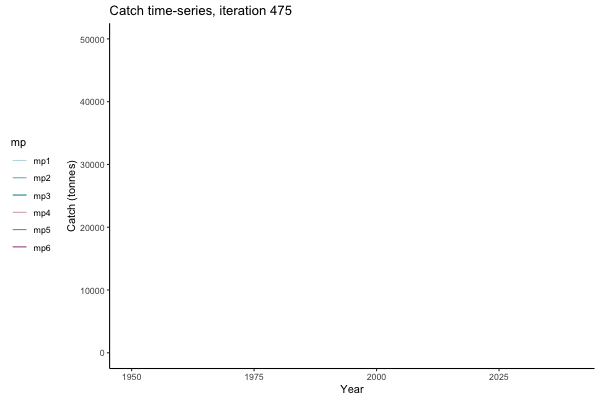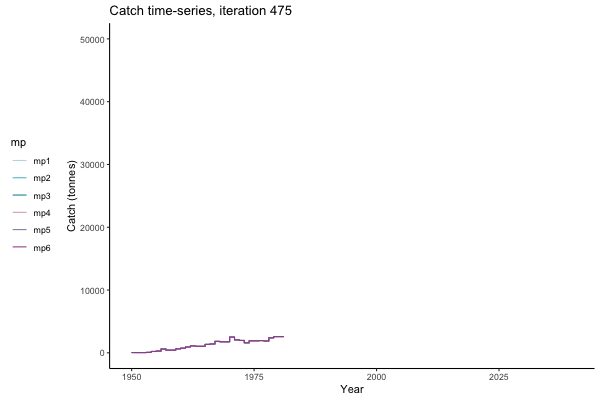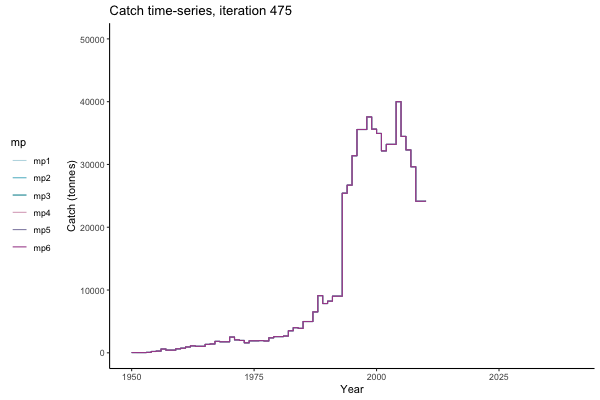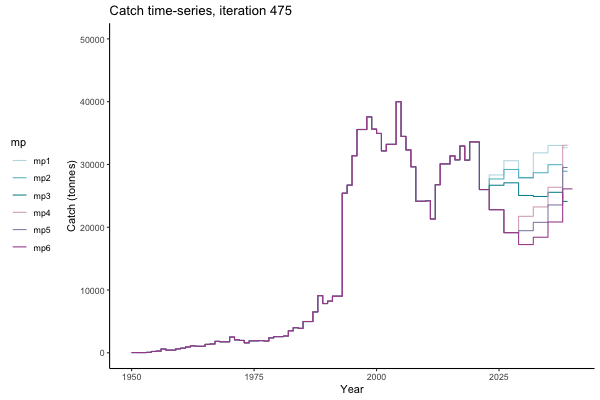
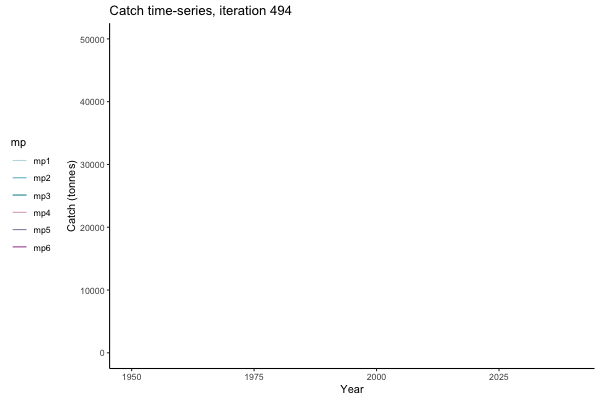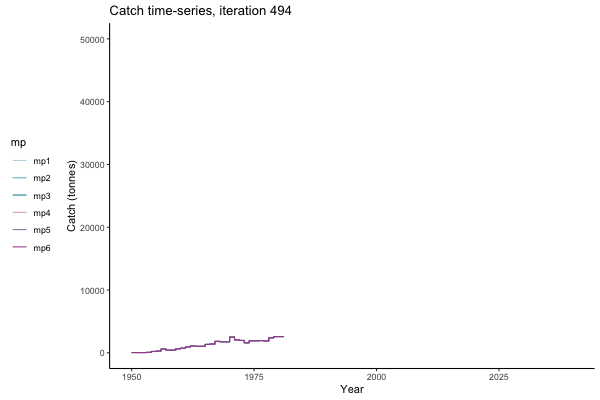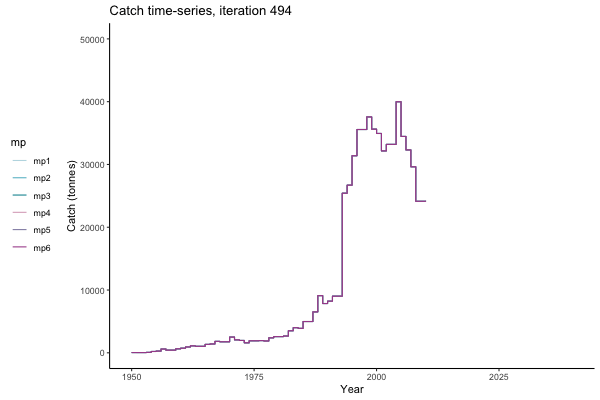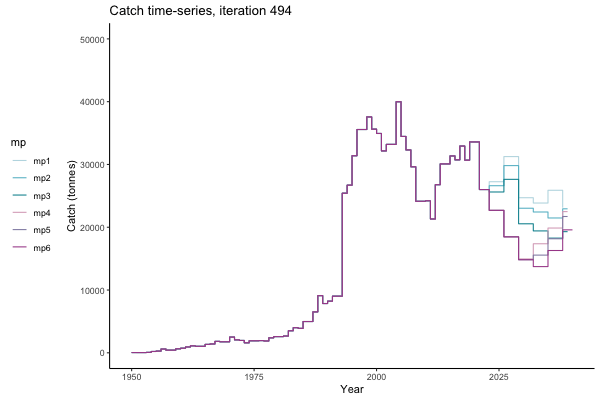
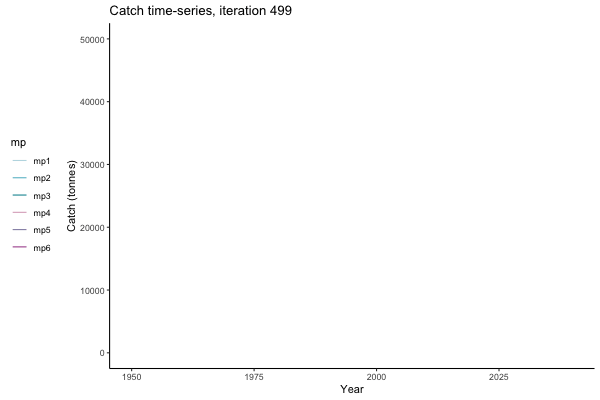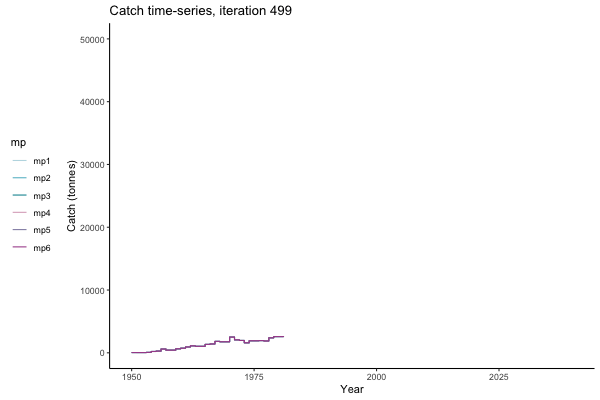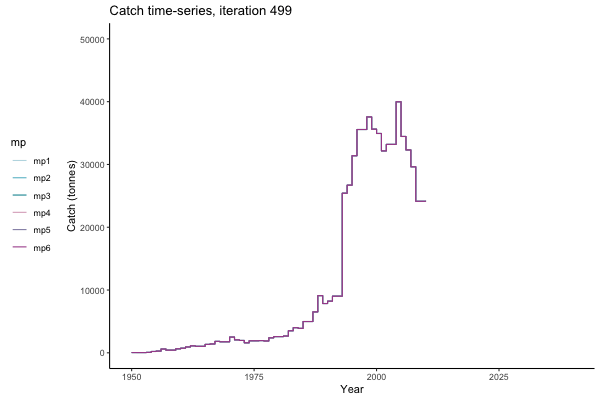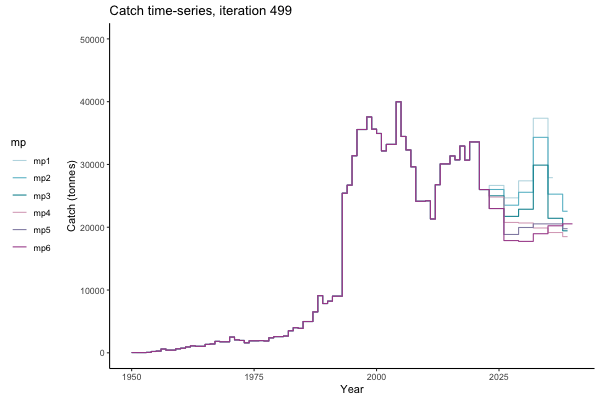
In the random simulation below (Catch / Biomass time-series, iteration 497), where it seems that if you want the highest catch (left), you should select MP4 (light pink).
![[ gif showing Catch time-series, iteration 497 ]](iotc/images/simulations-gifs/Catch497.gif)
Catch time-series, iteration 497
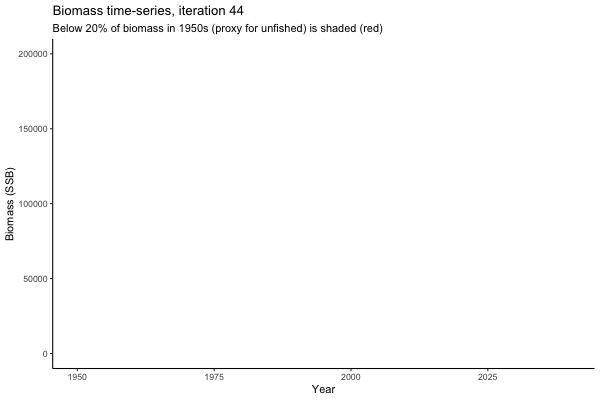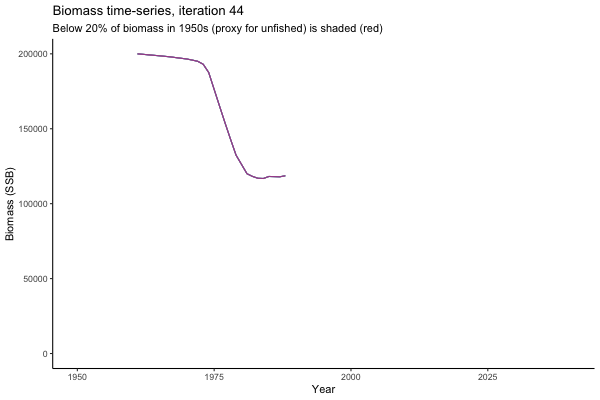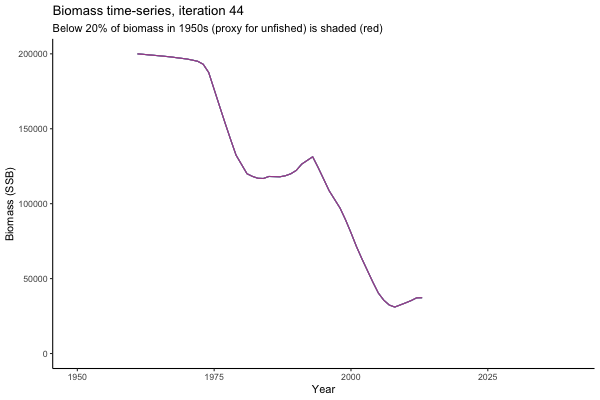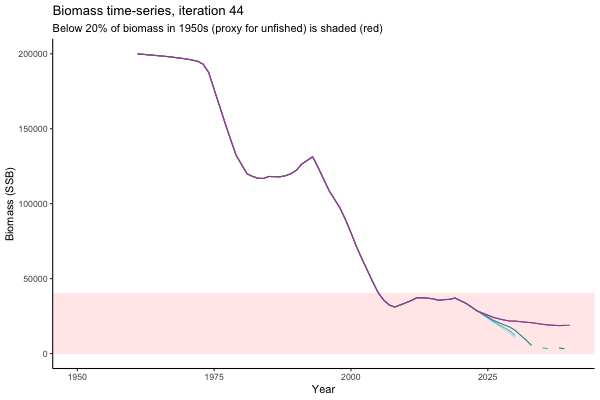
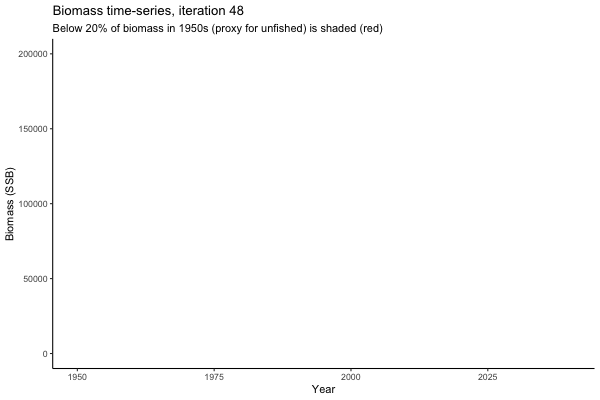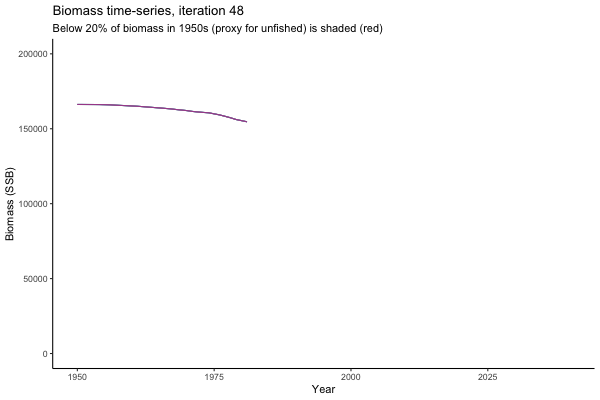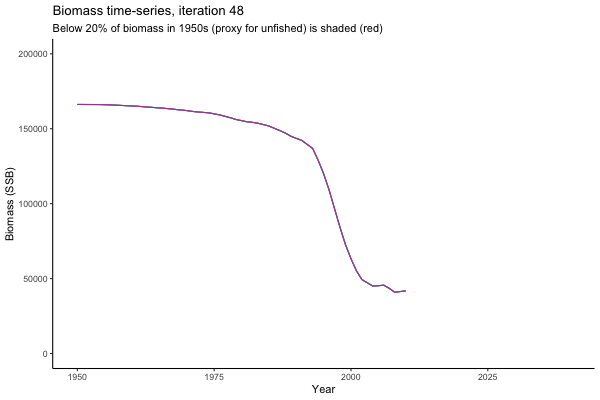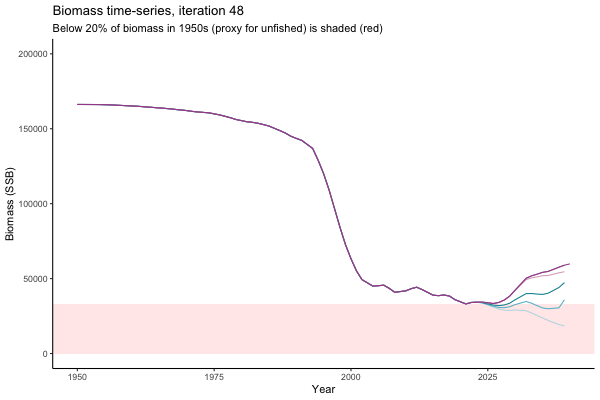
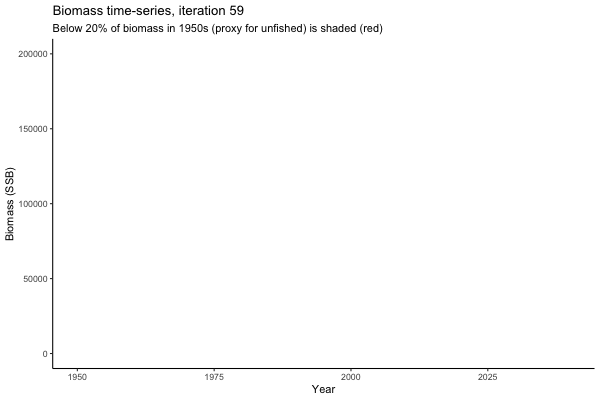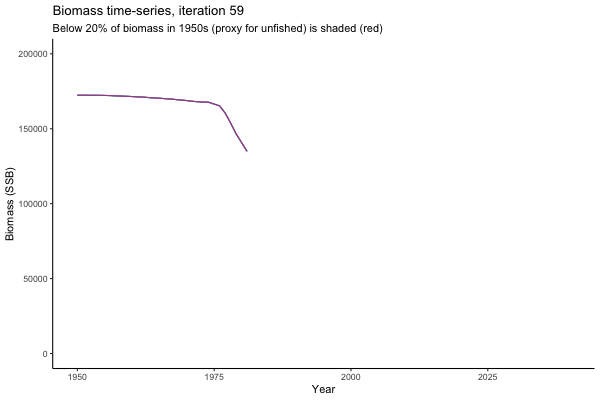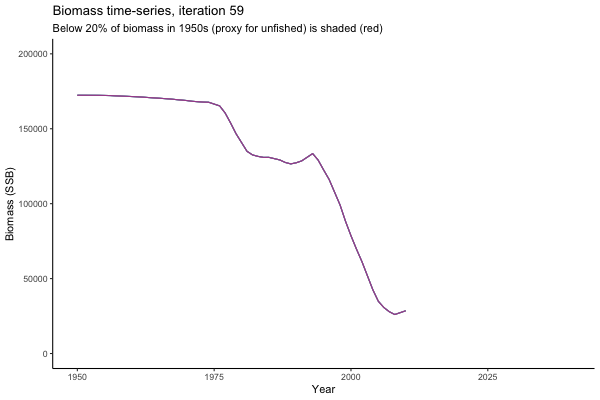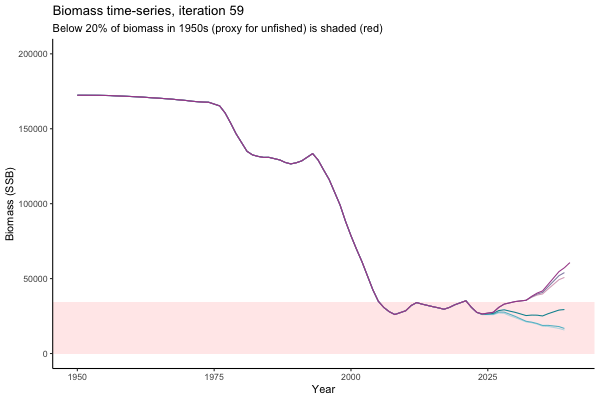
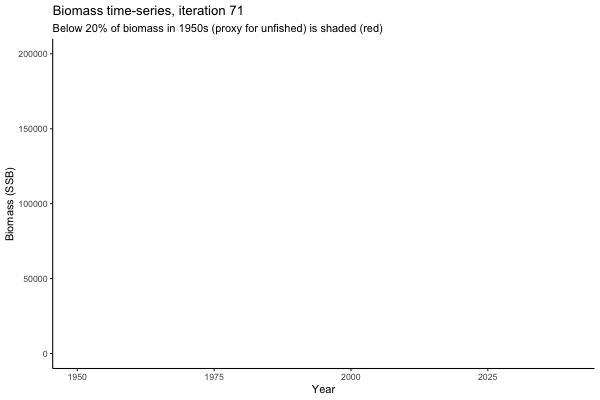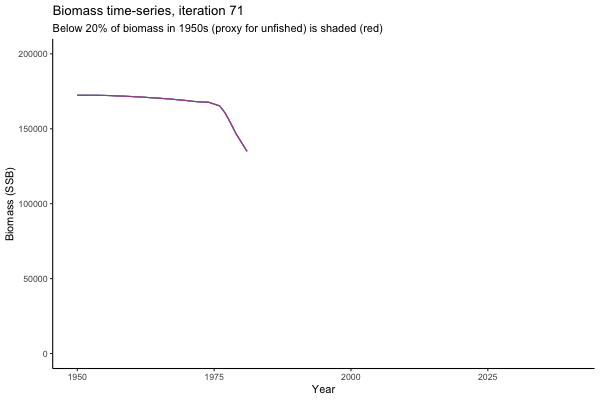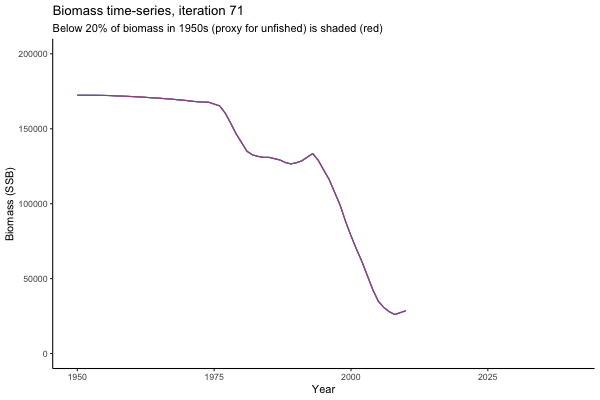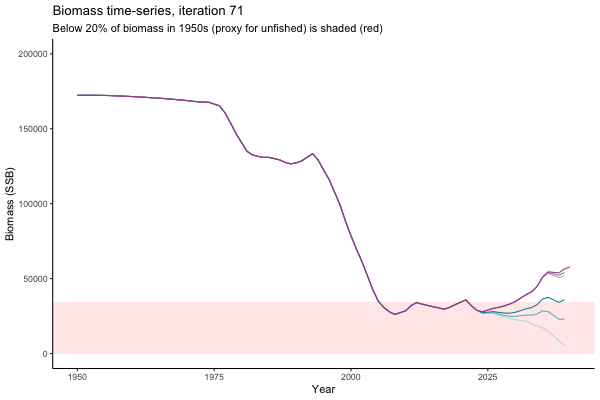
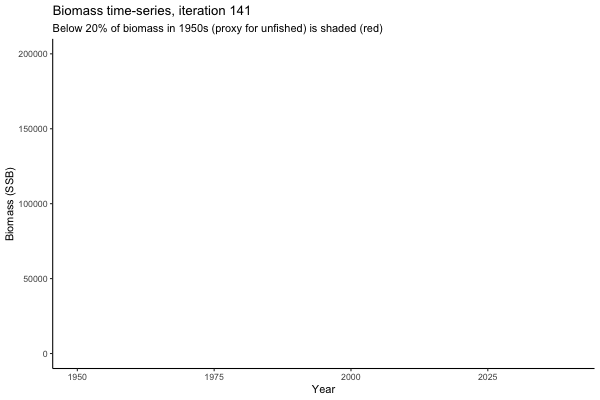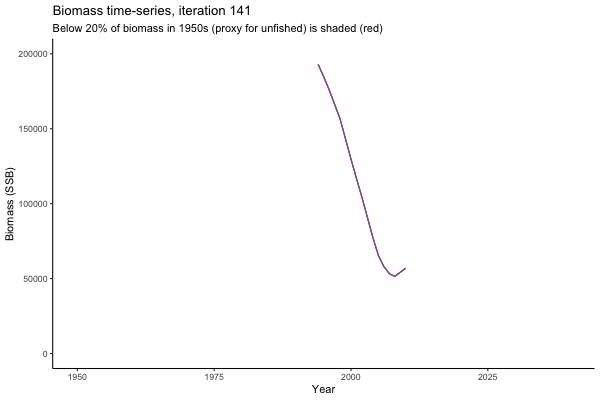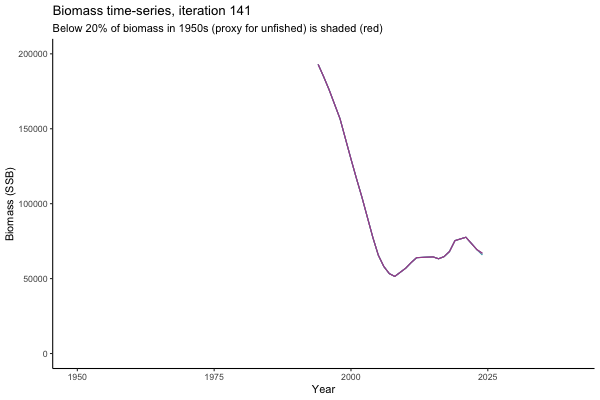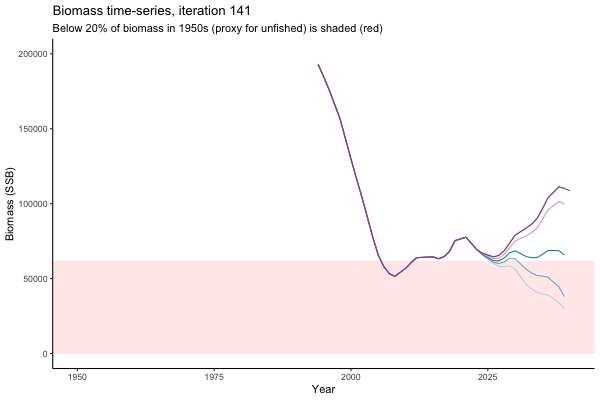
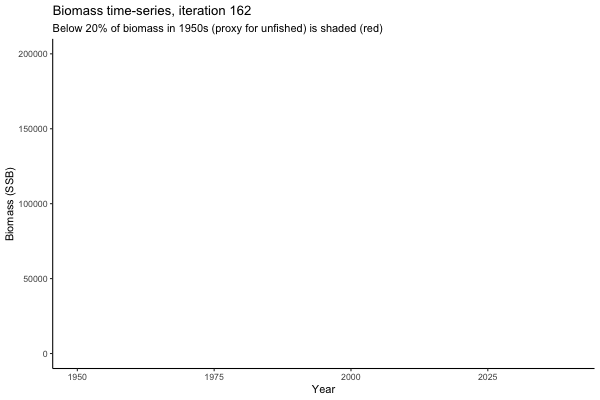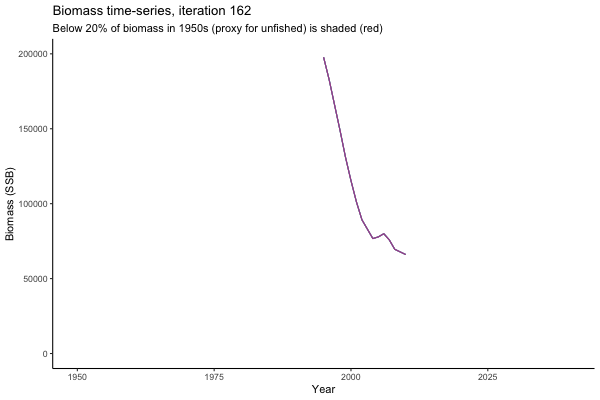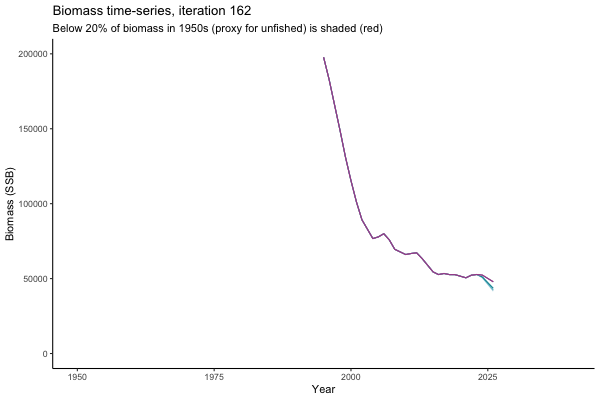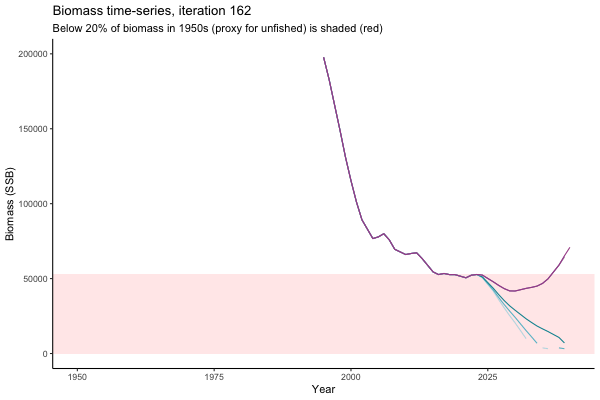
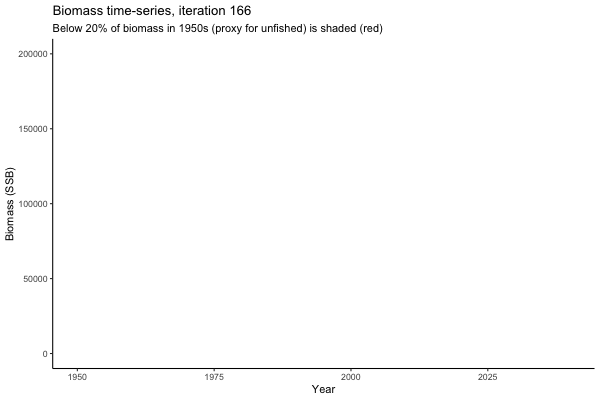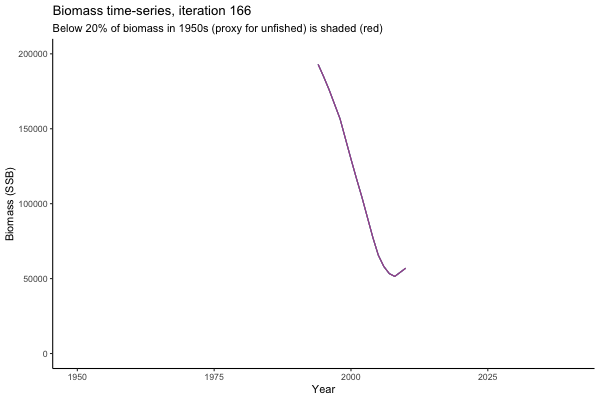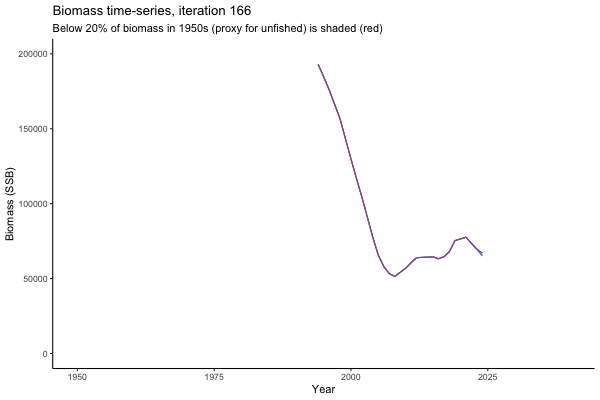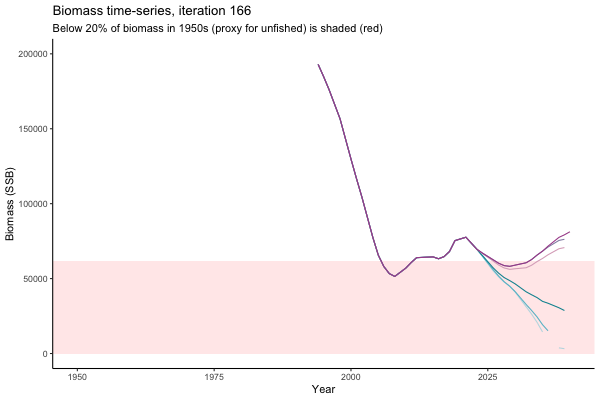
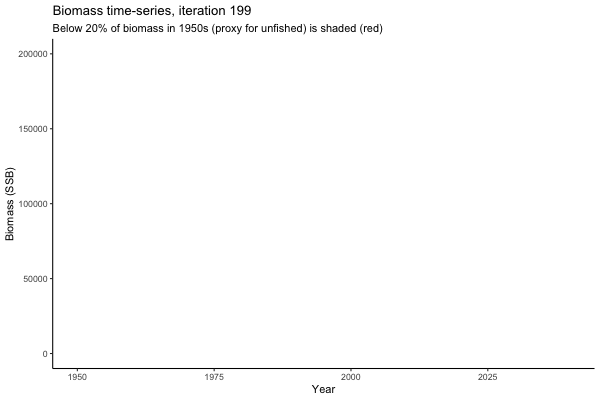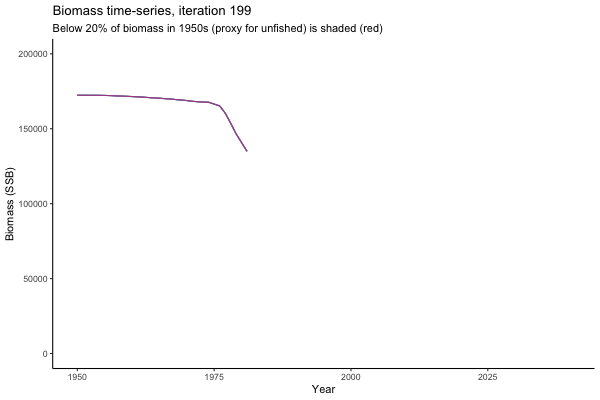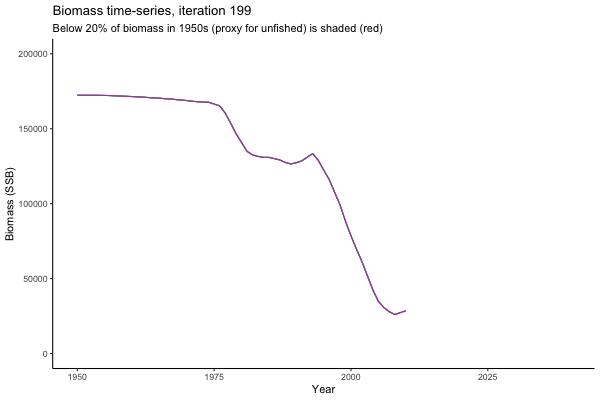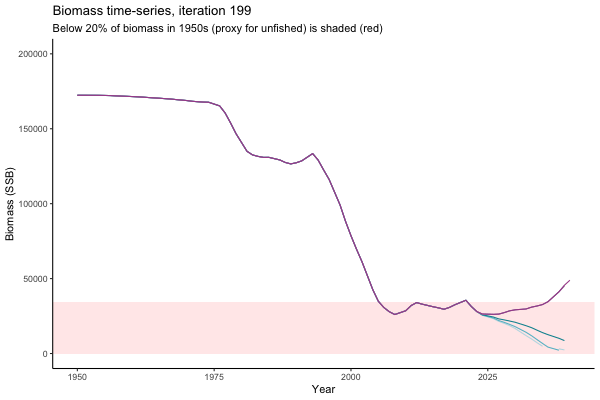
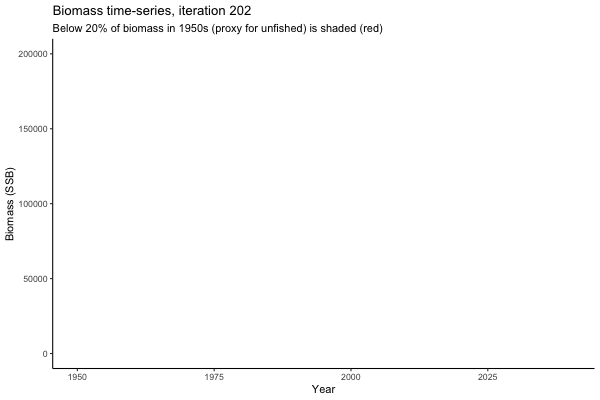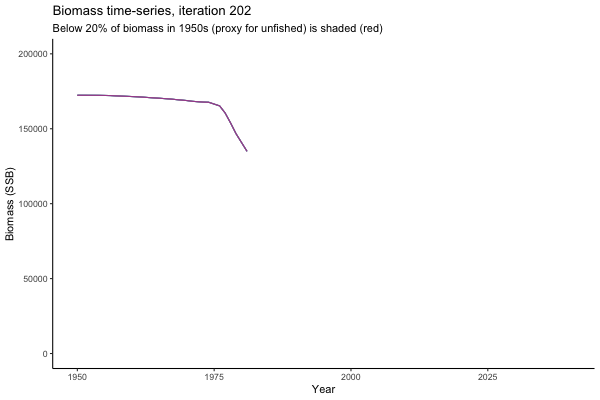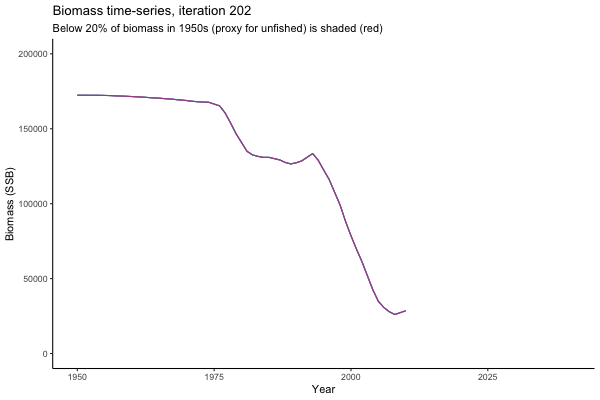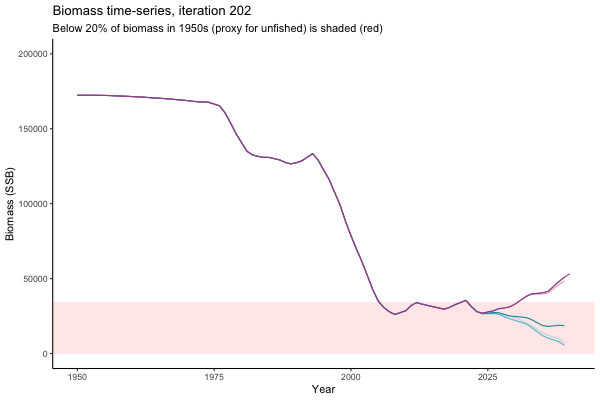
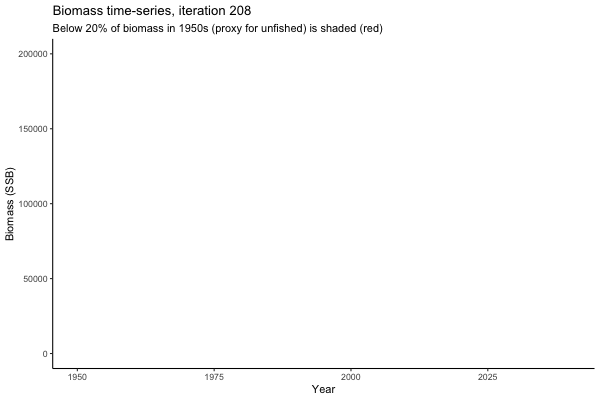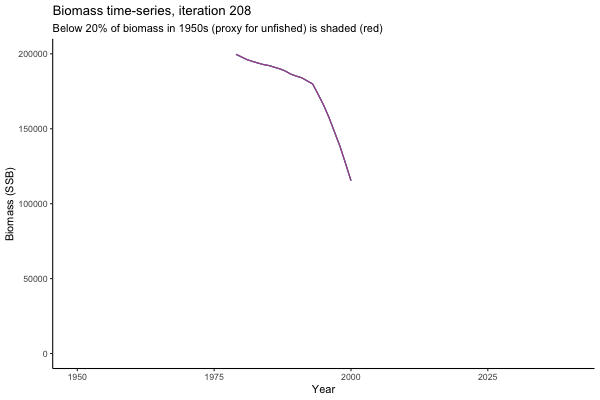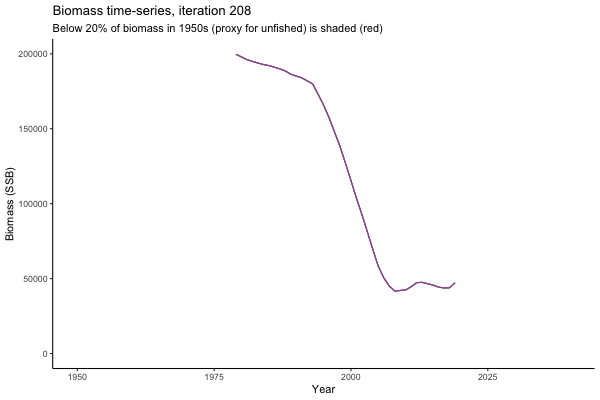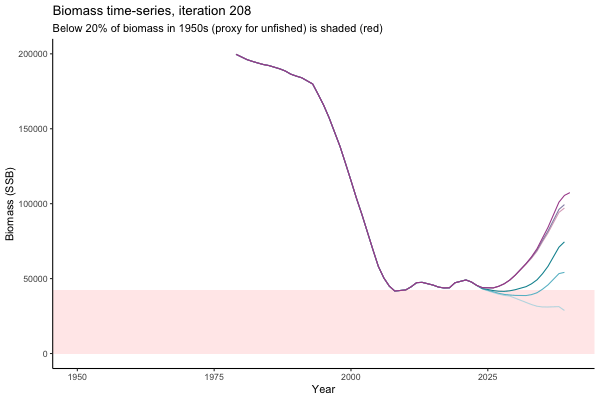
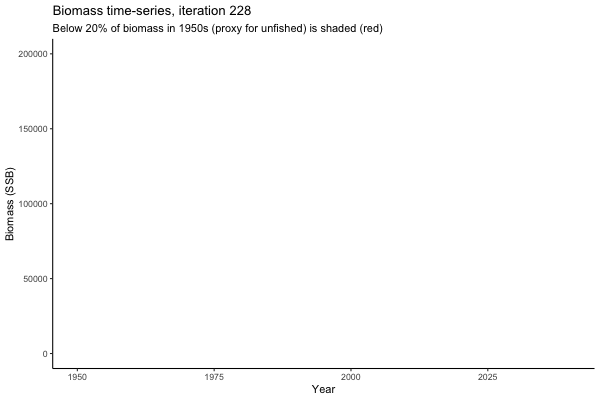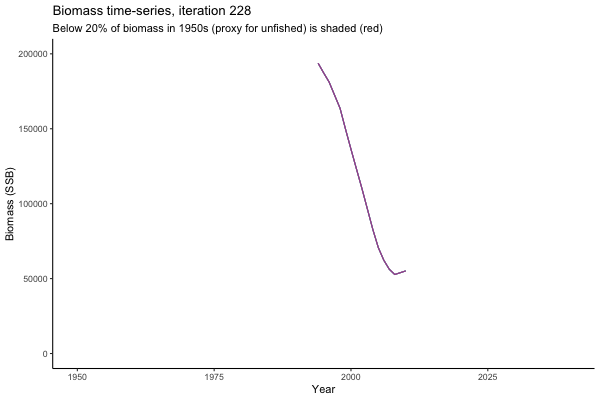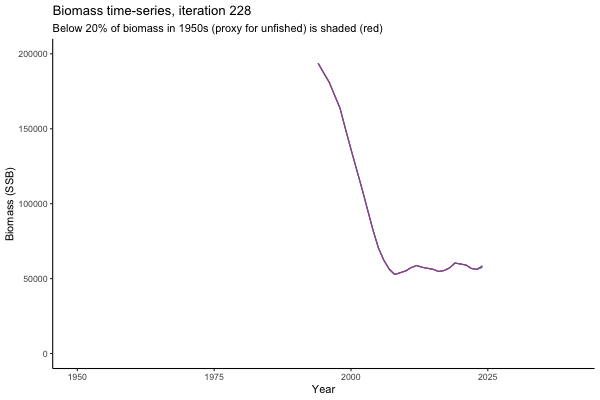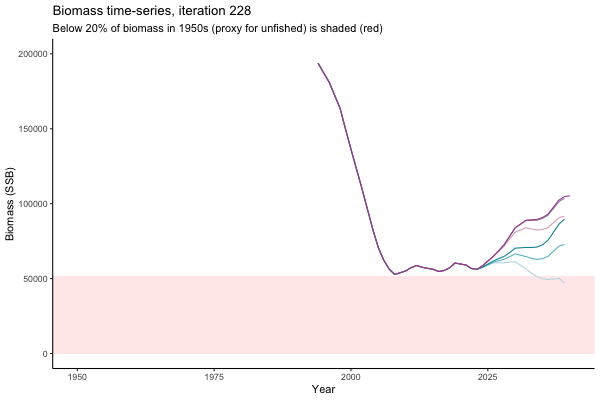
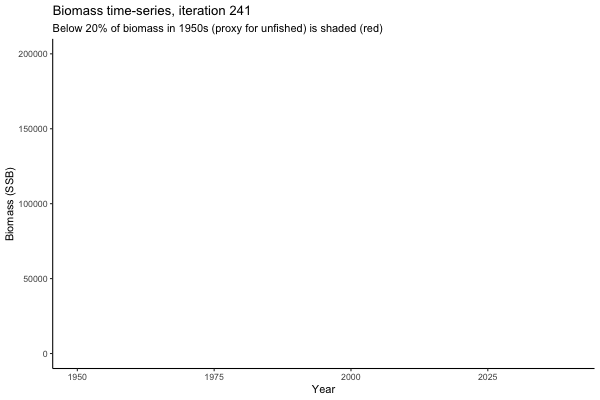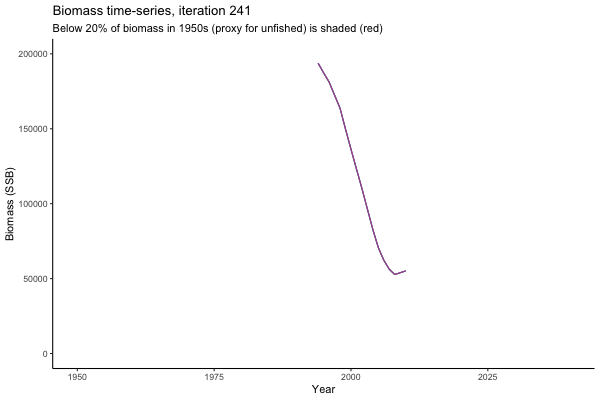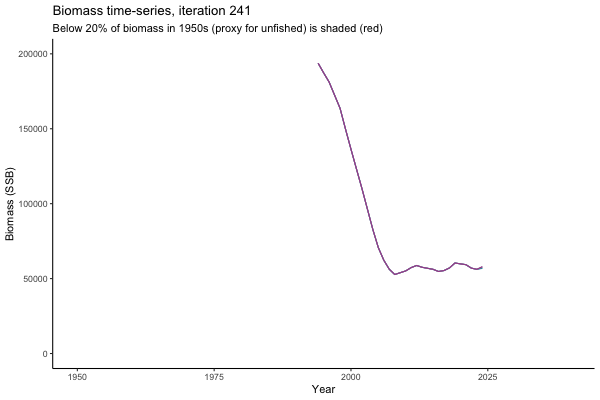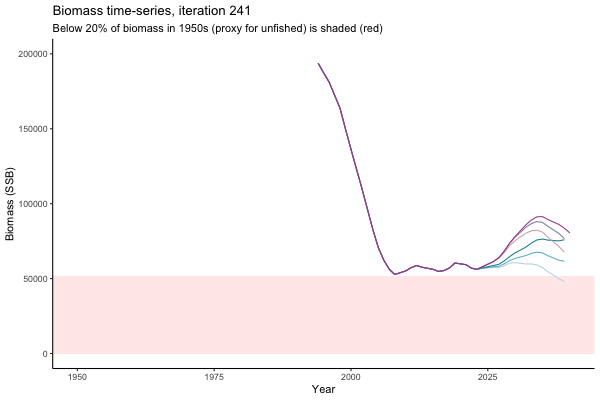
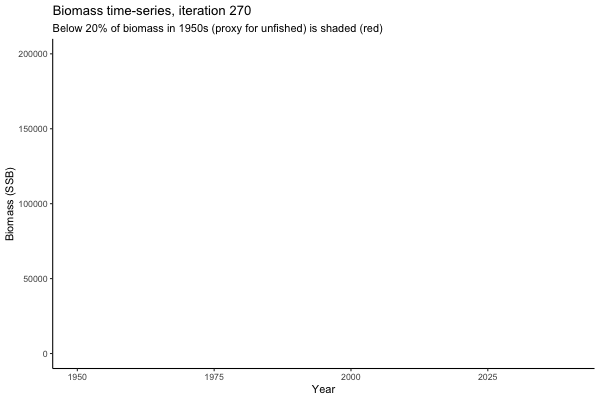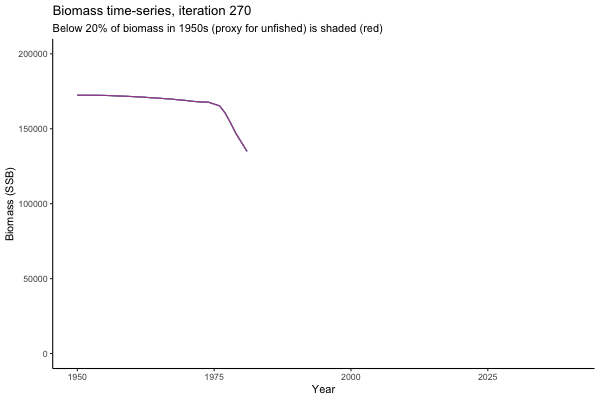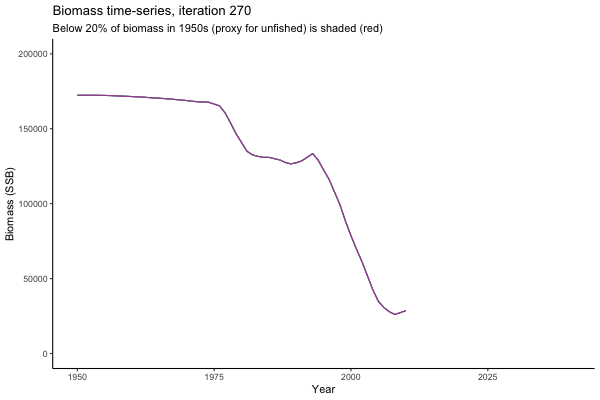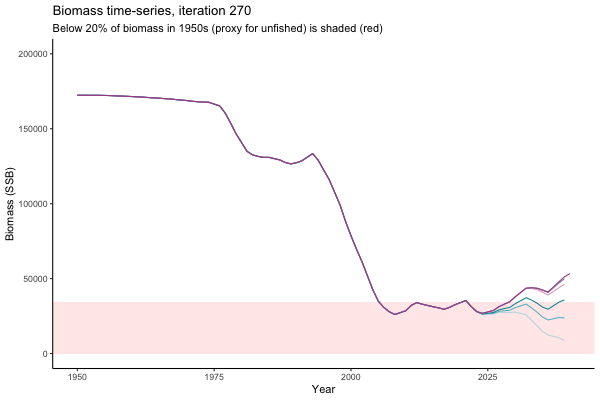
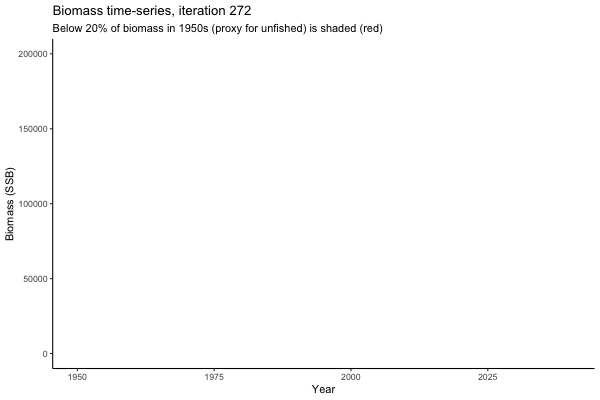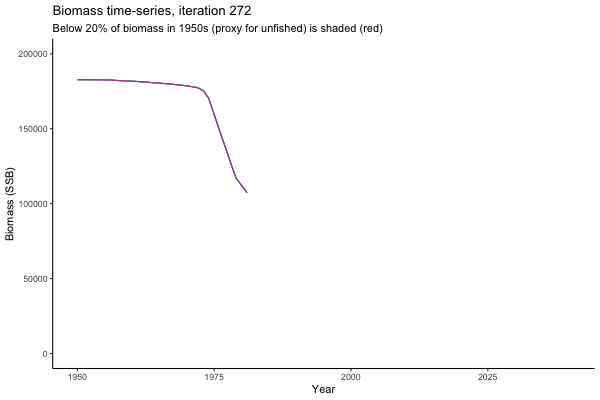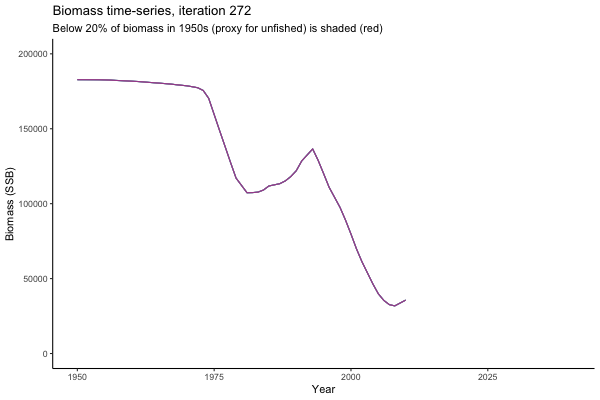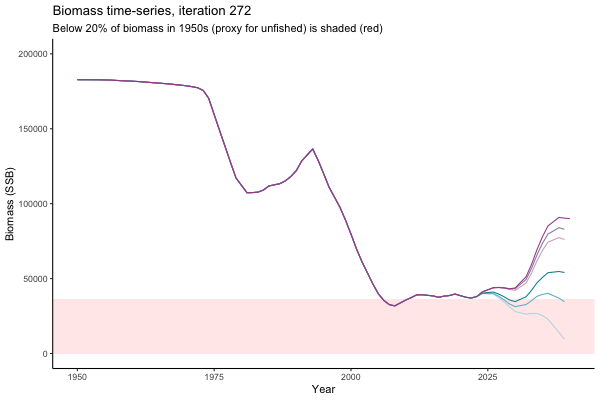
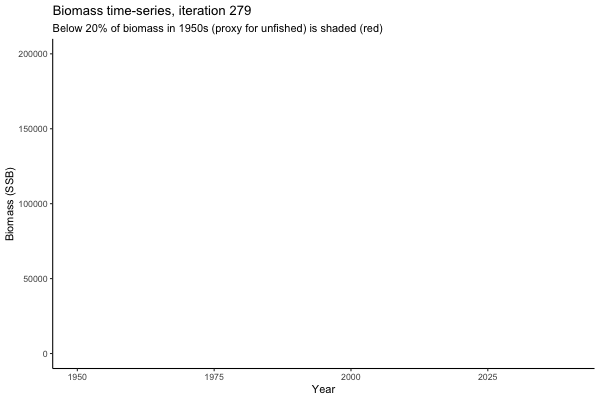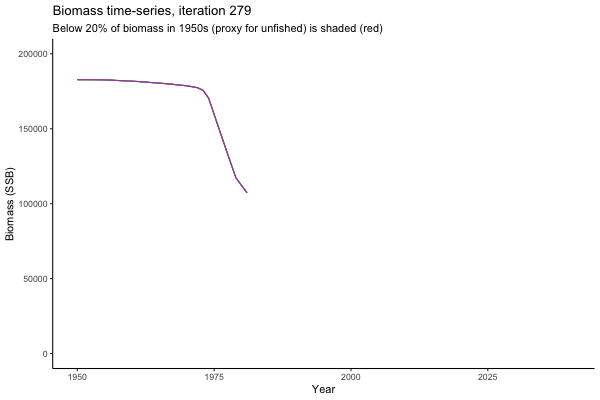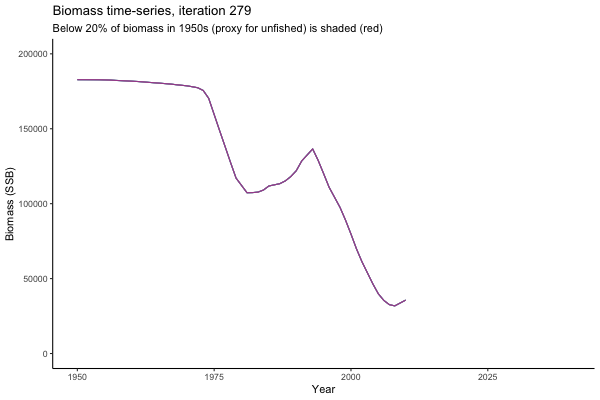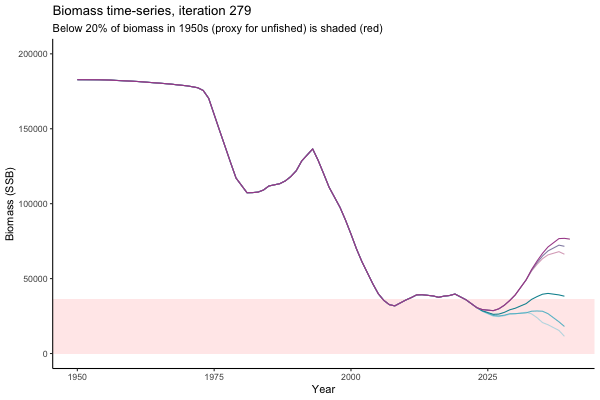
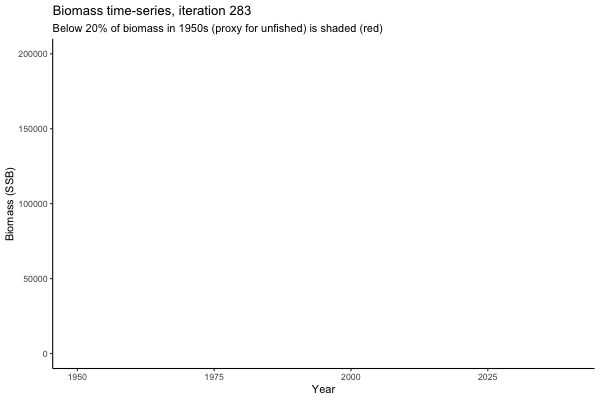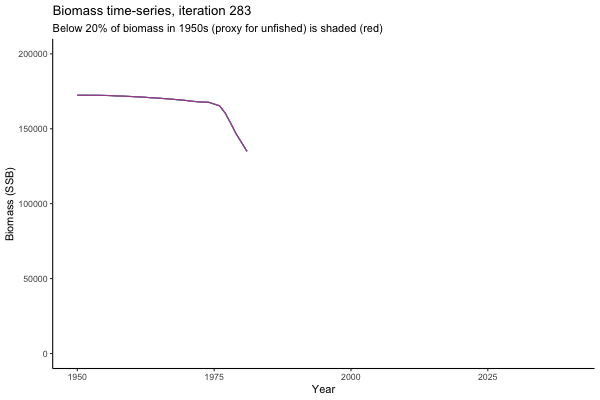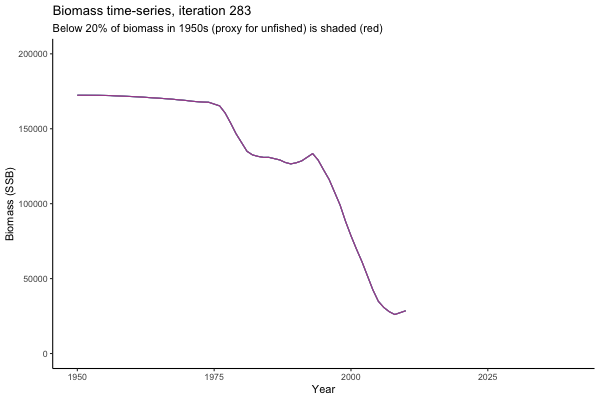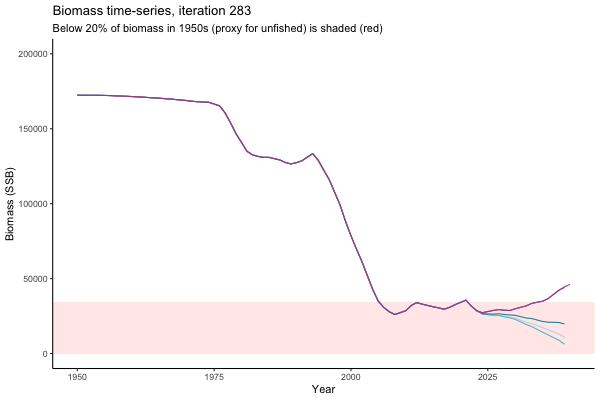
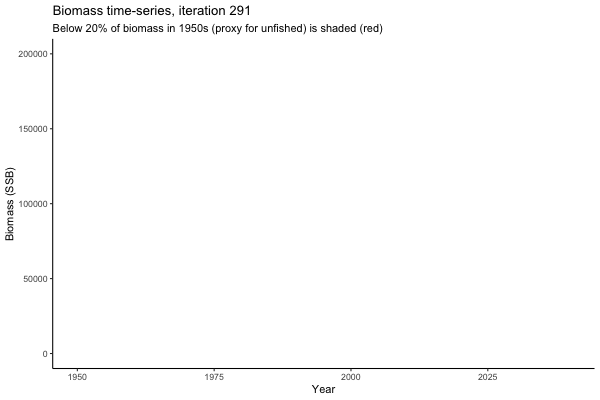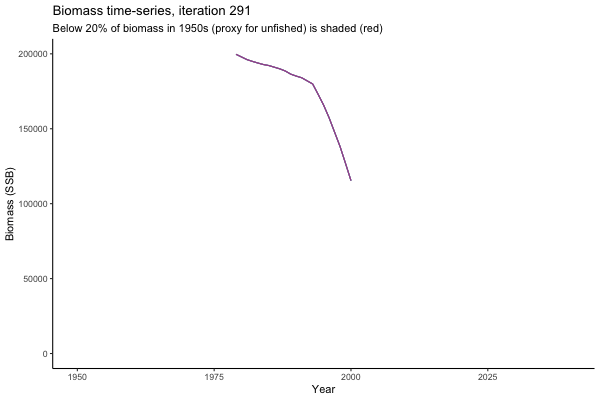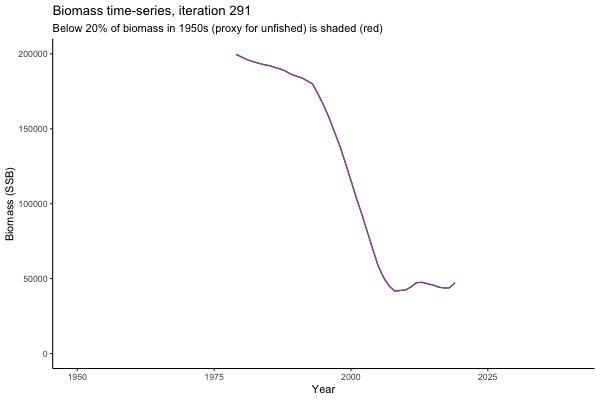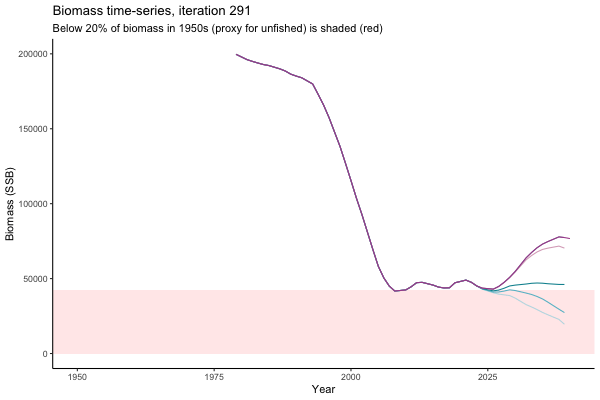
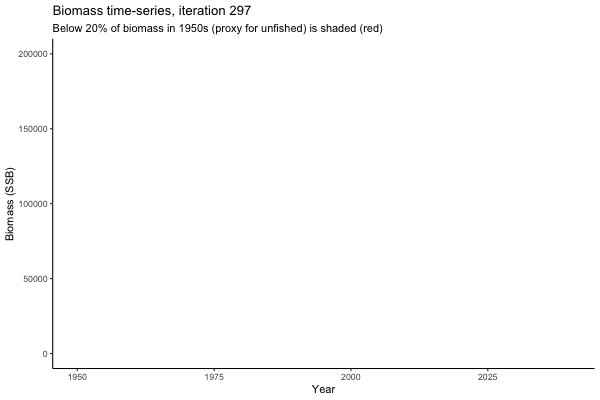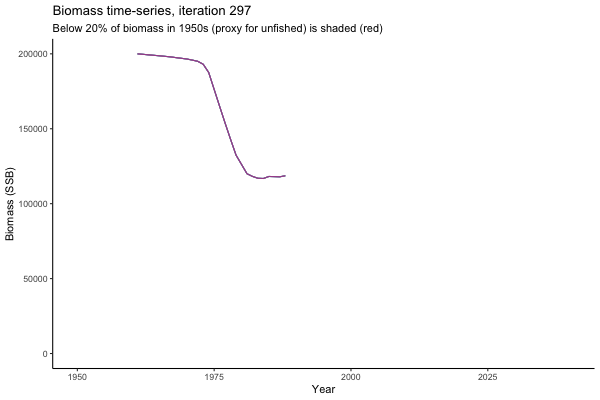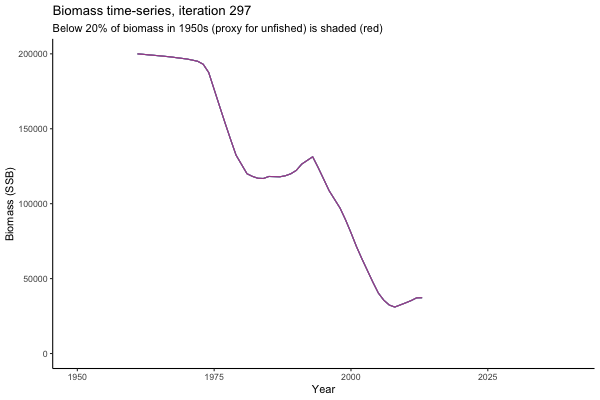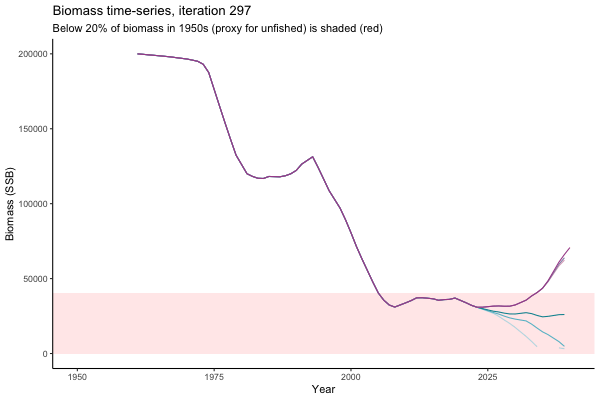
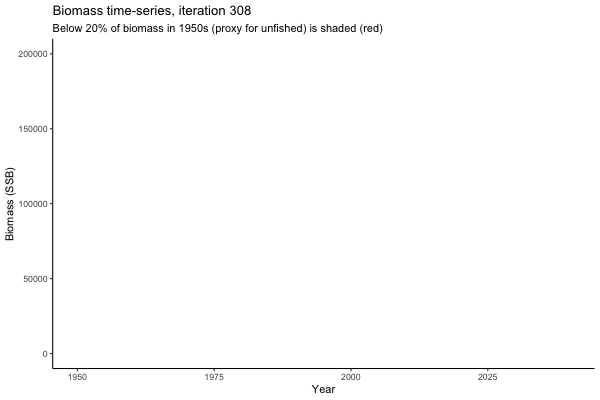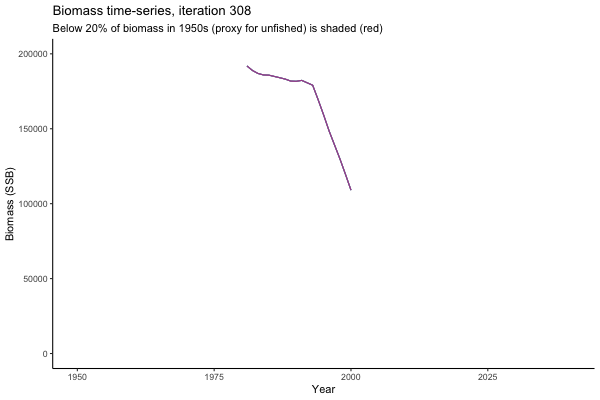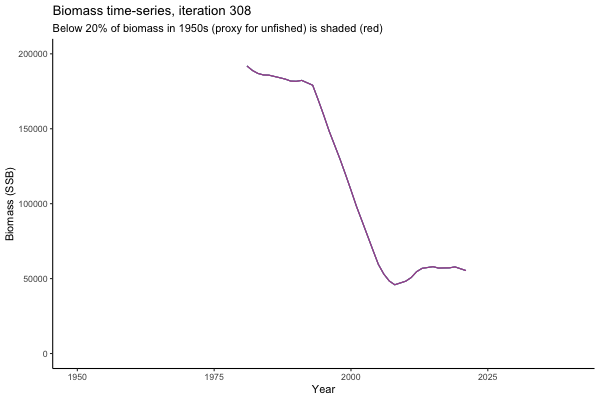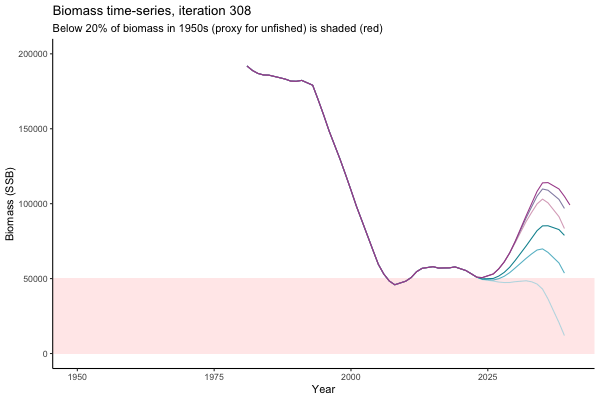
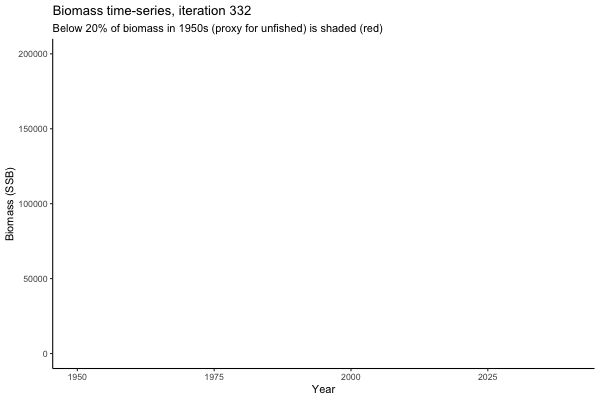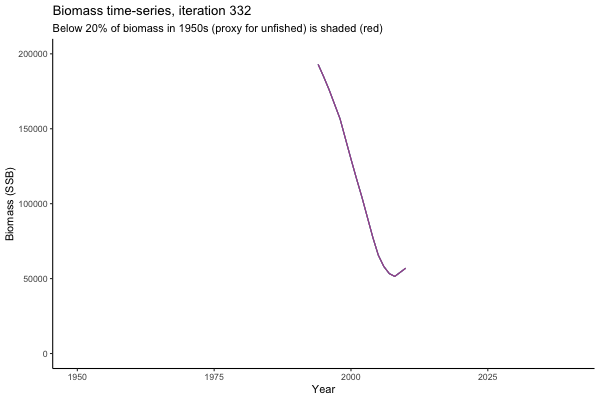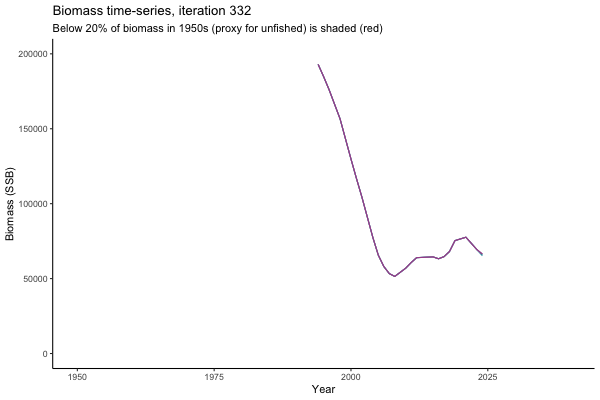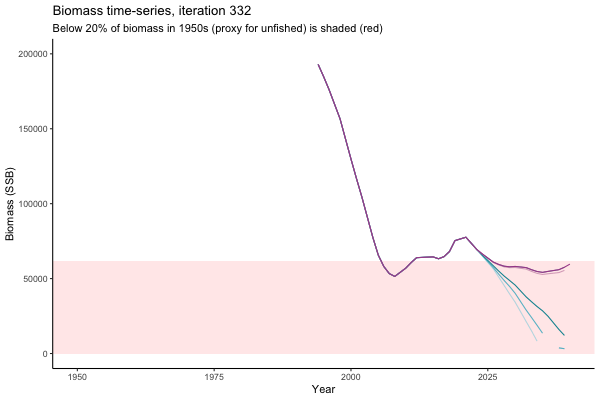
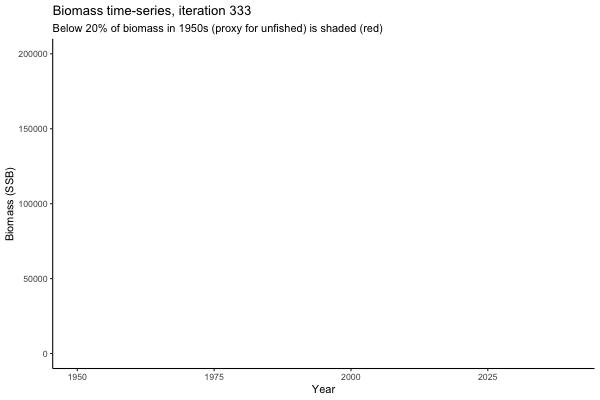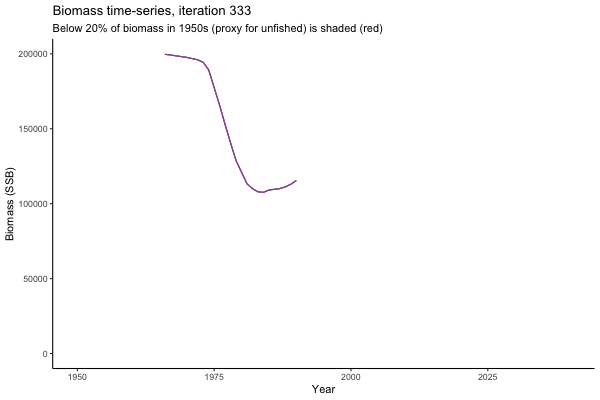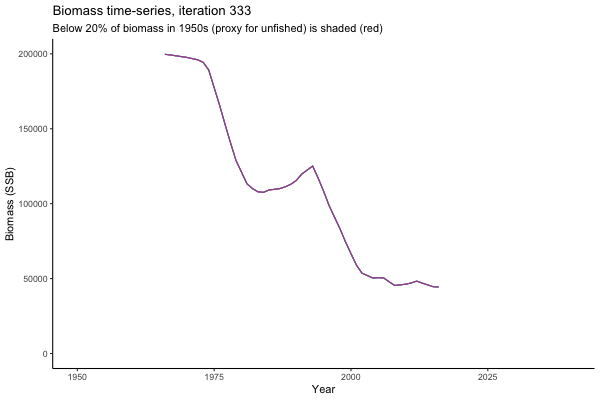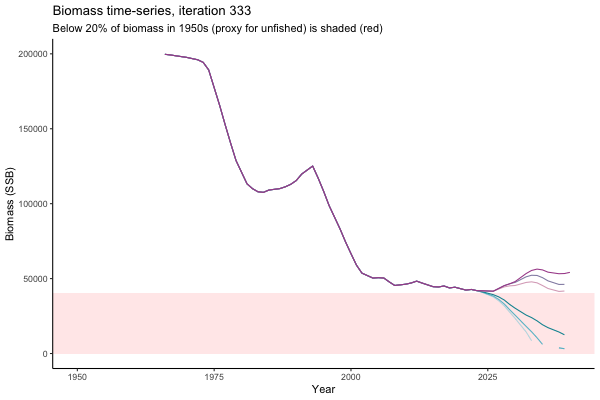
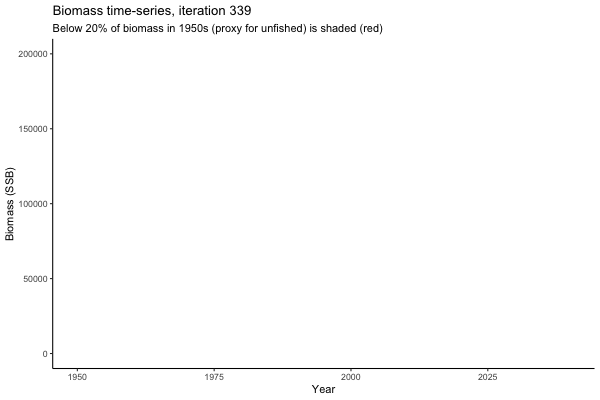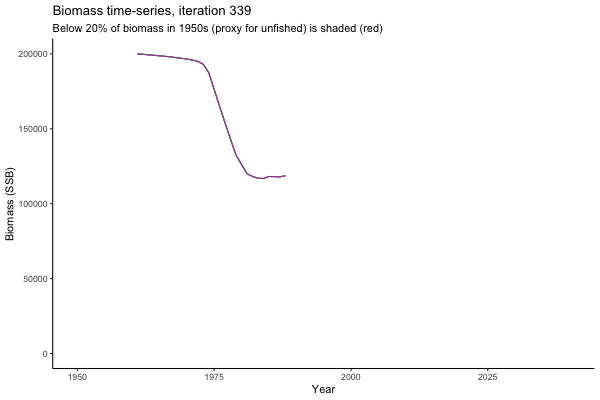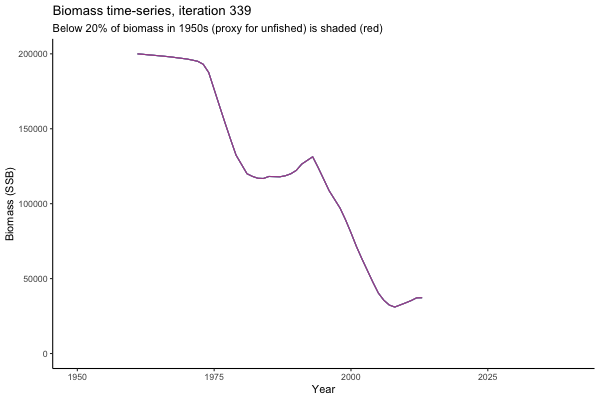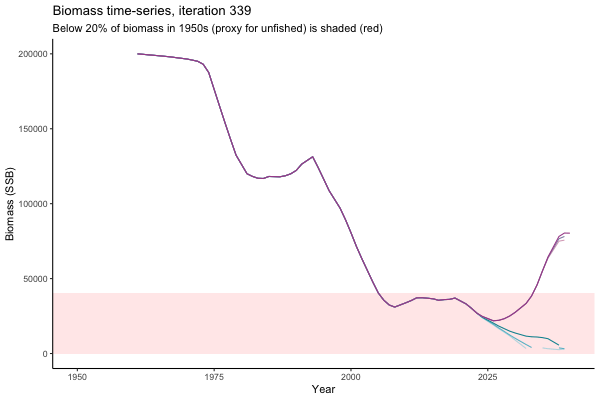
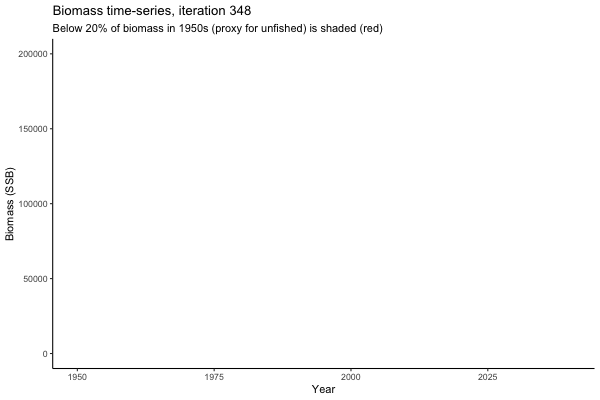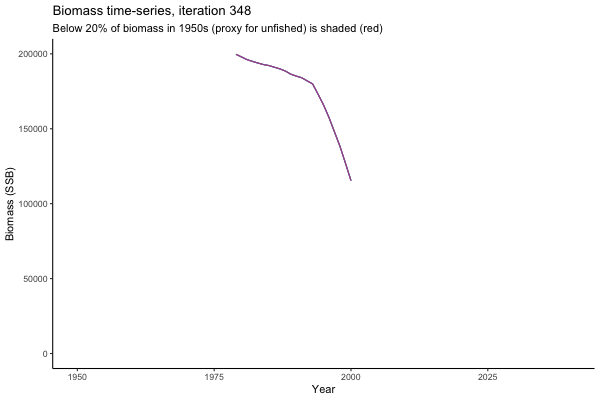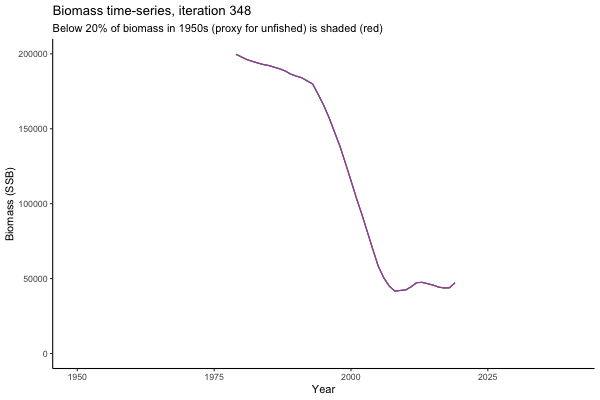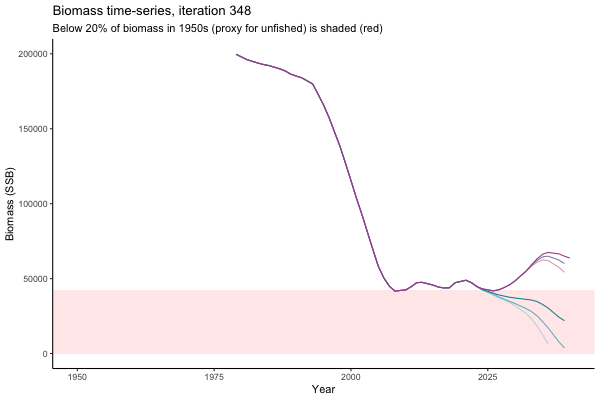
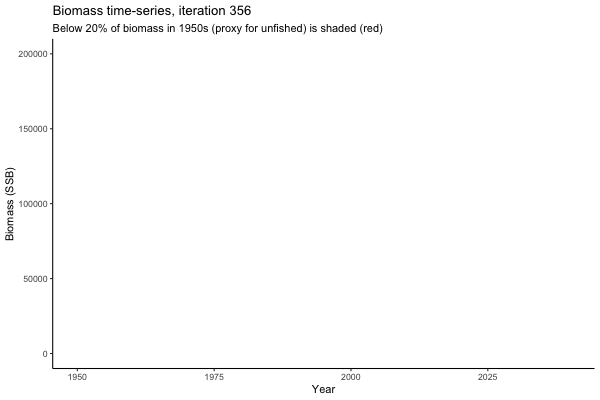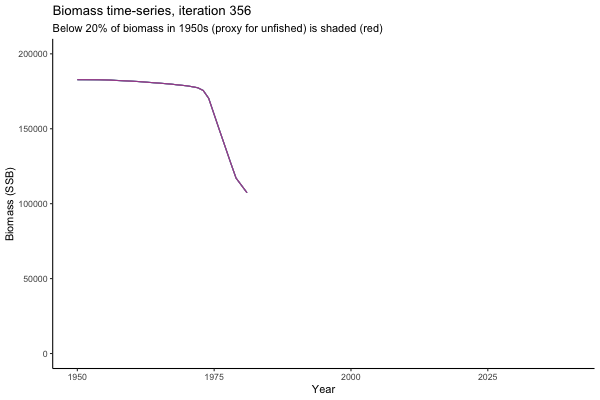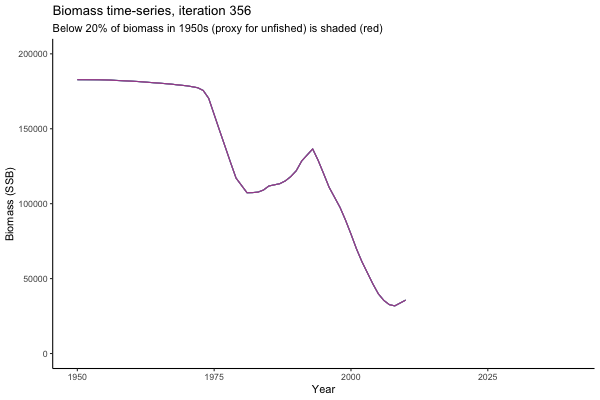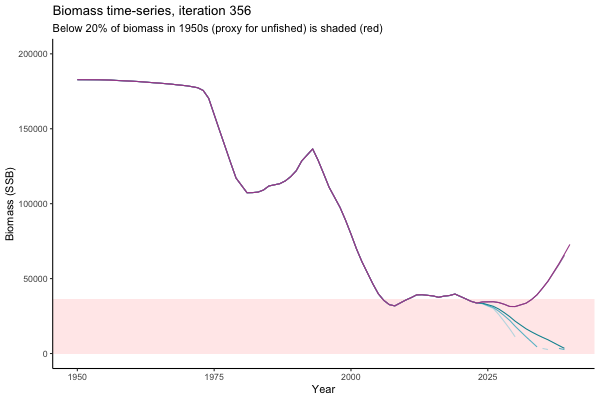
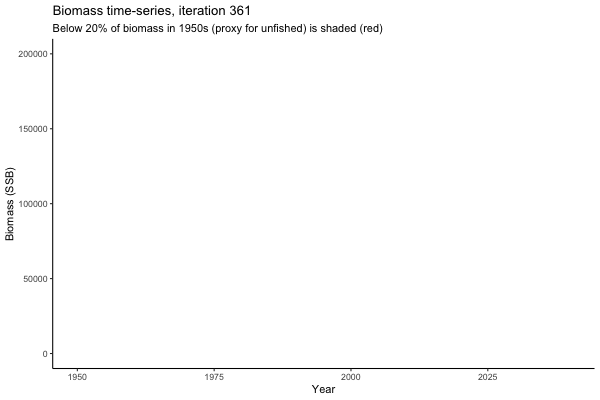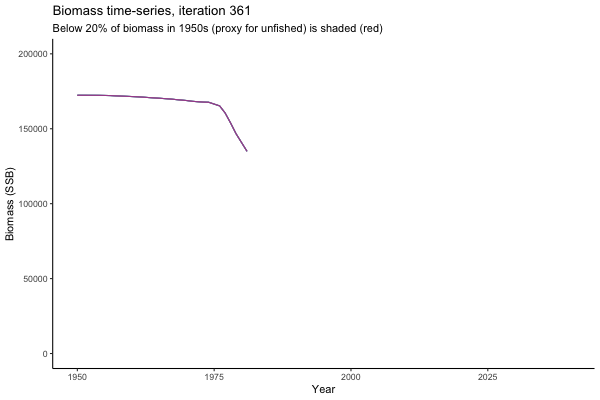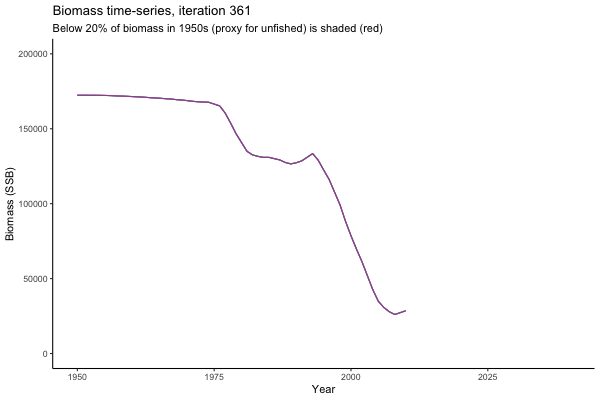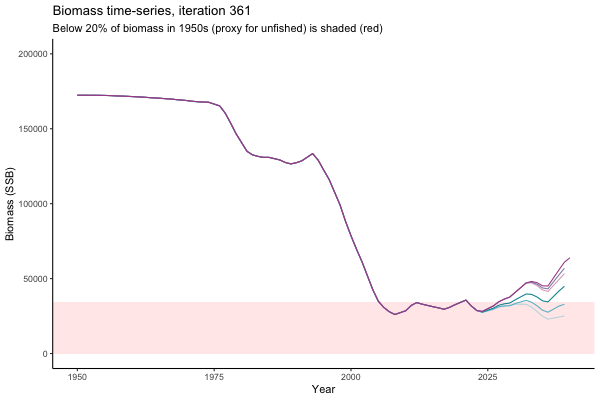
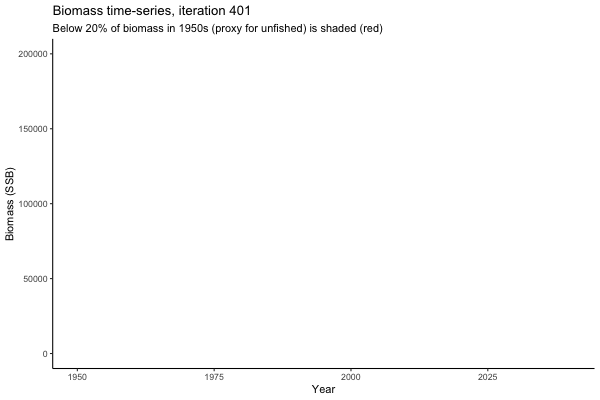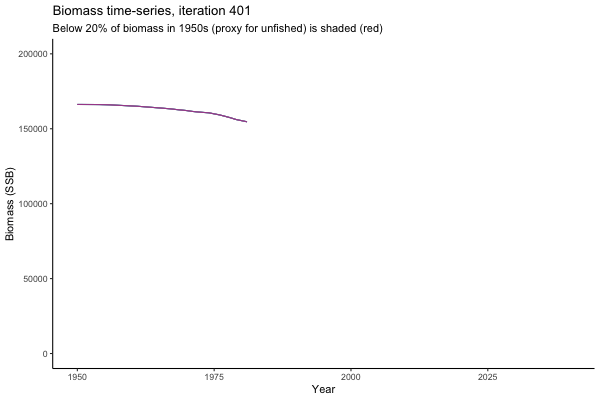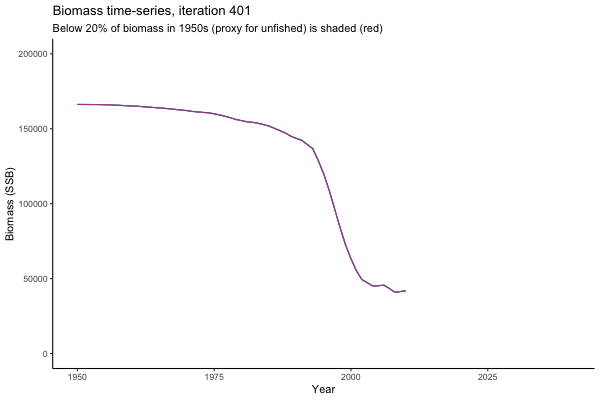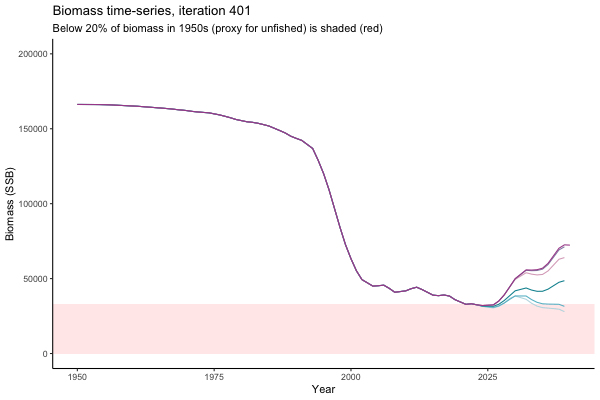
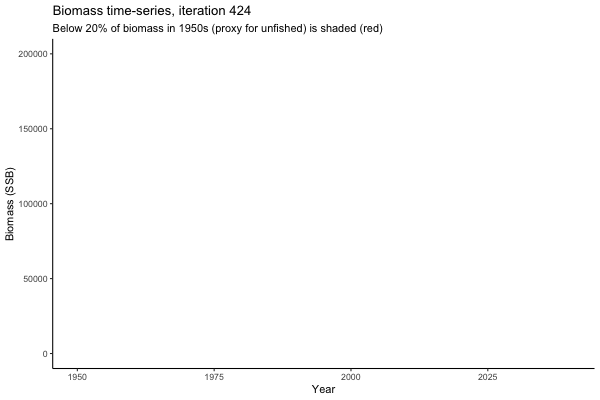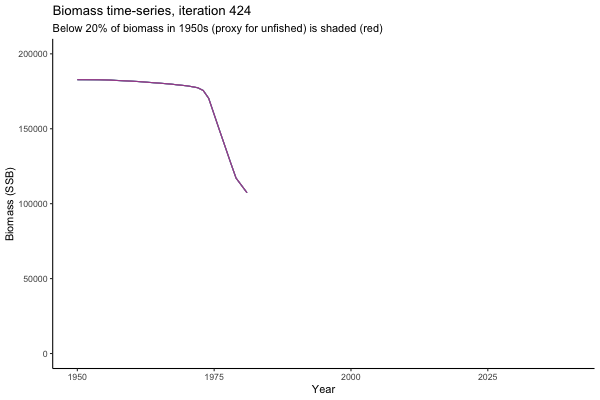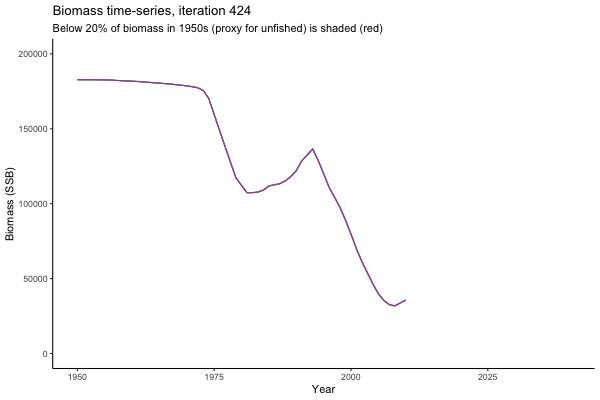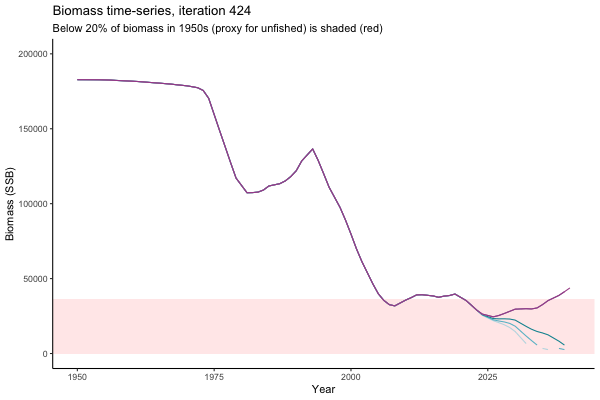
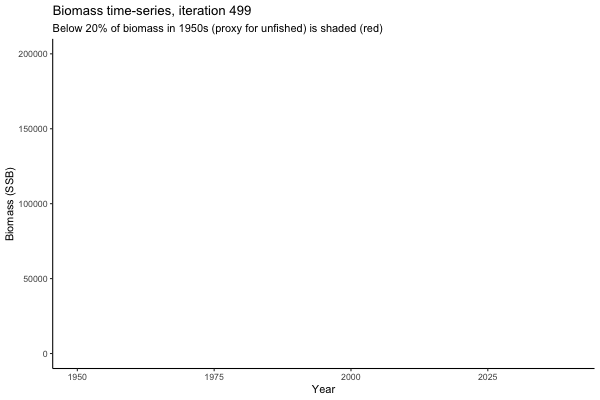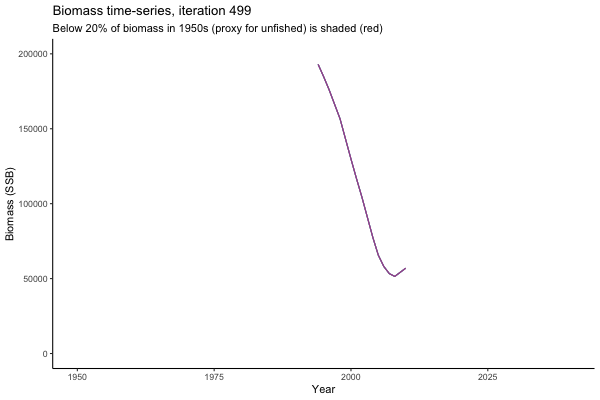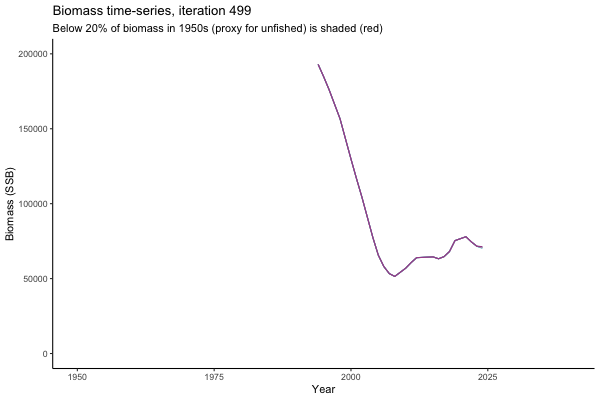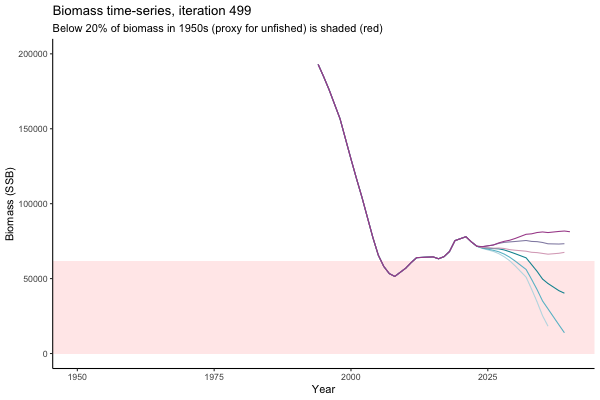
![[ gif showing Biomass time-series, iteration 497]](iotc/images/simulations-gifs/Biom497.gif)
Biomass time-series, iteration 497
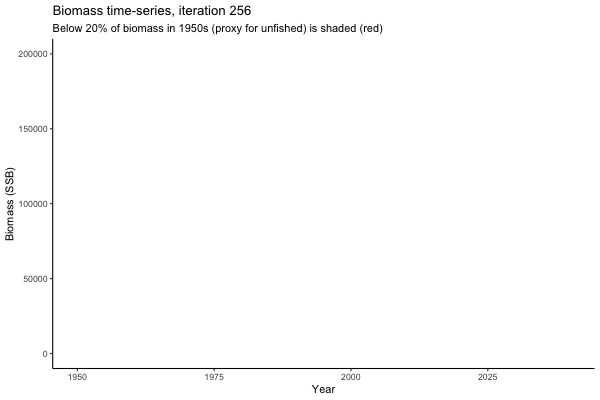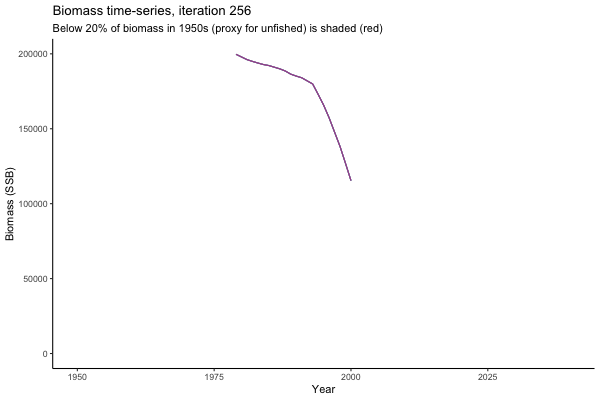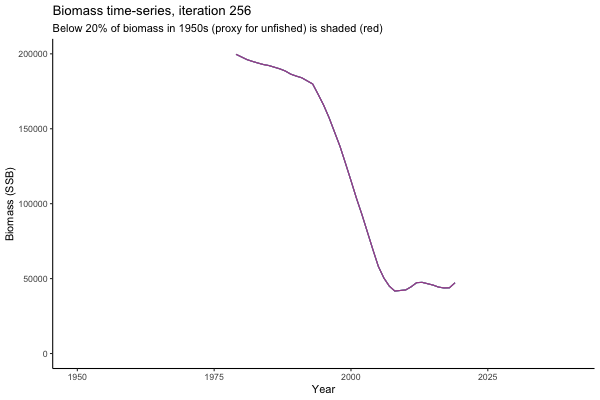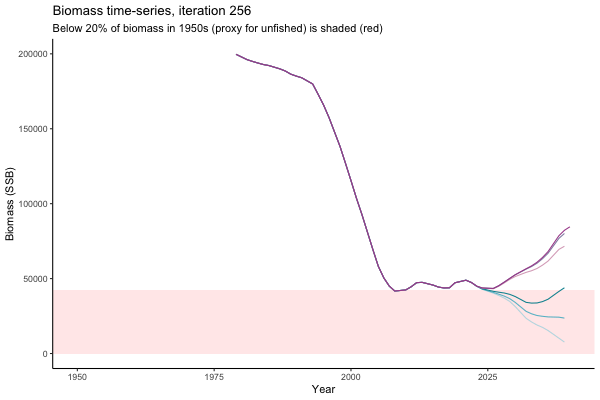
However, looking at a different random simulation (below, Catch / Biomass time-series, iteration 14), MP4 appears as one of your worst options in terms of catch.
![[ gif showing Catch time-series, iteration 14 ]](iotc/images/simulations-gifs/Catch14.gif)
Catch time-series, iteration 14
![[ gif showing Biomass time-series, iteration 14 ]](iotc/images/simulations-gifs/Biom14.gif)
Biomass time-series, iteration 14
Not only are the futures different for each iteration, but also the past — representing different plausible historical values of biomass. Catches (left) are observations, and are fixed in this MSE example.
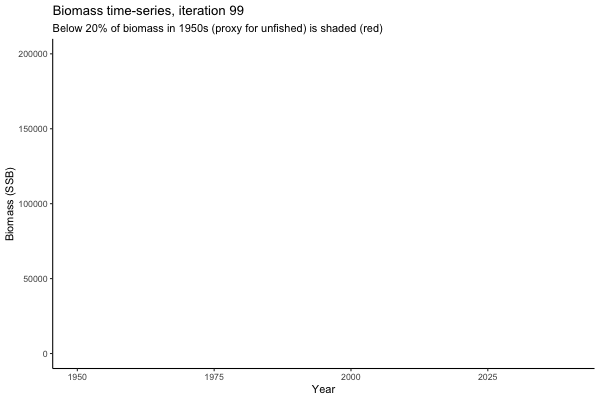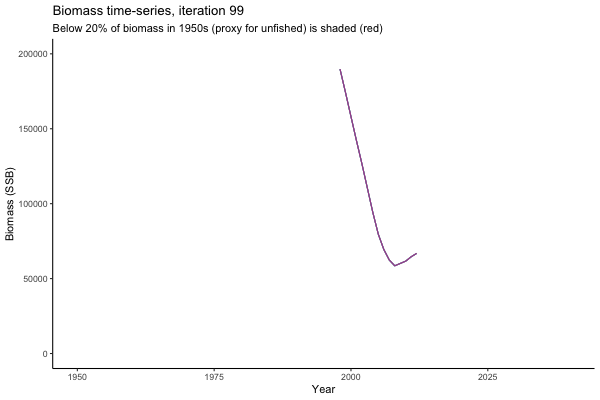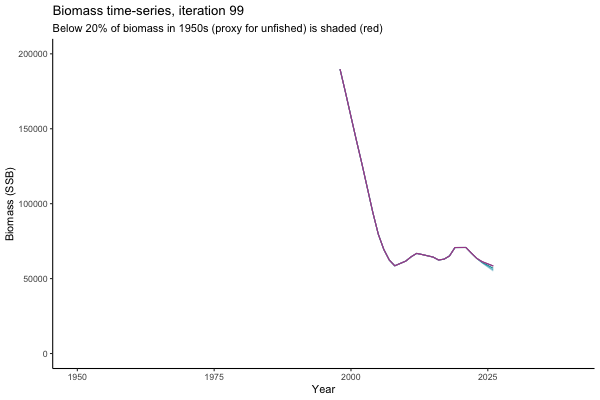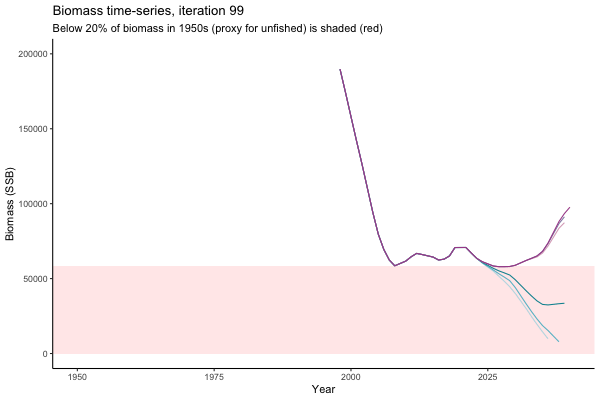
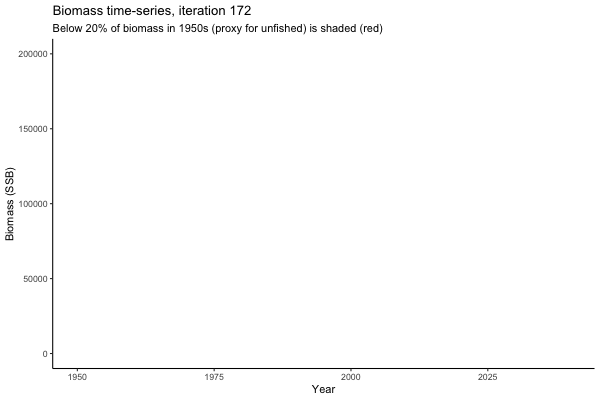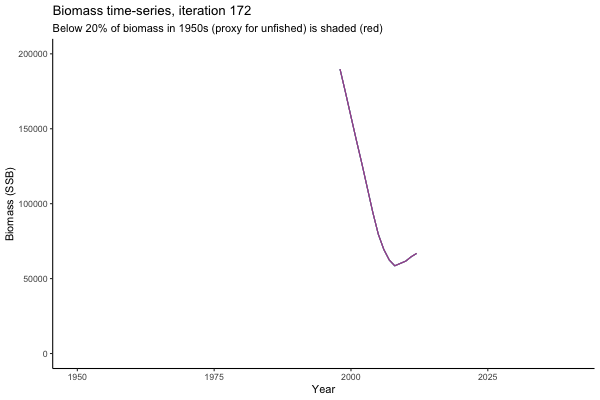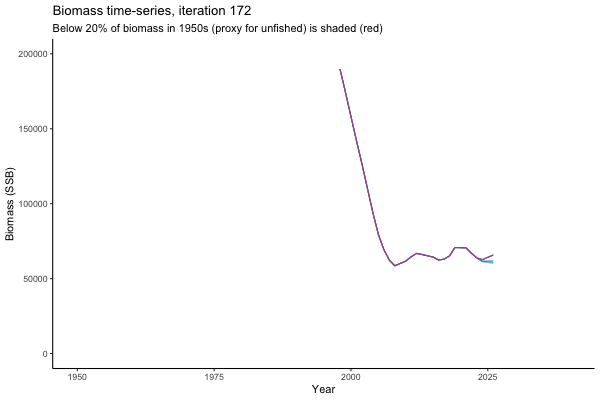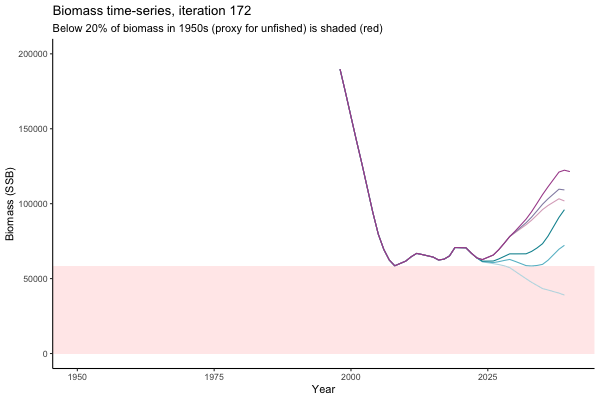
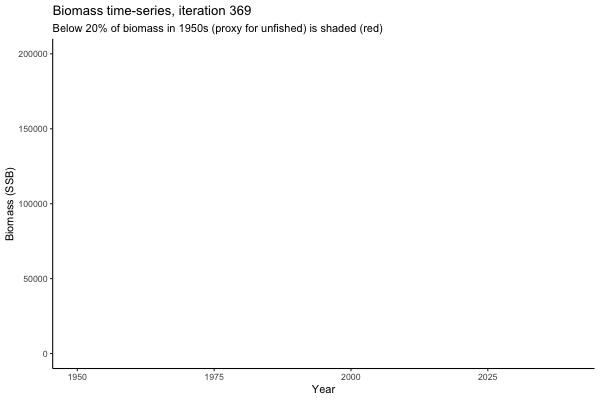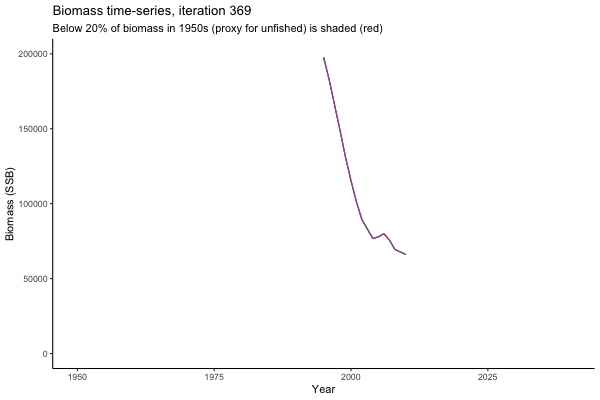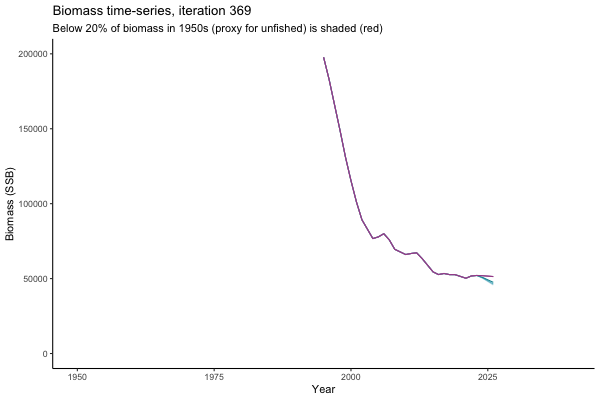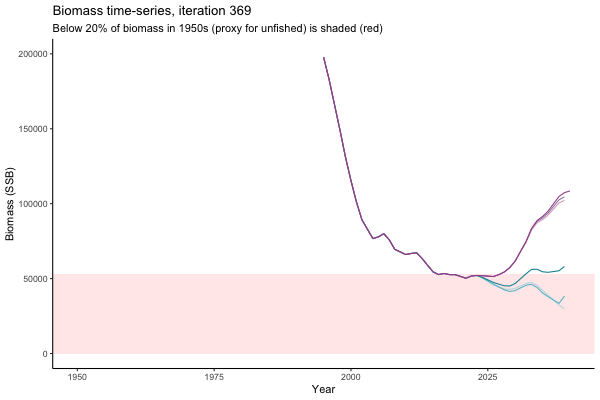
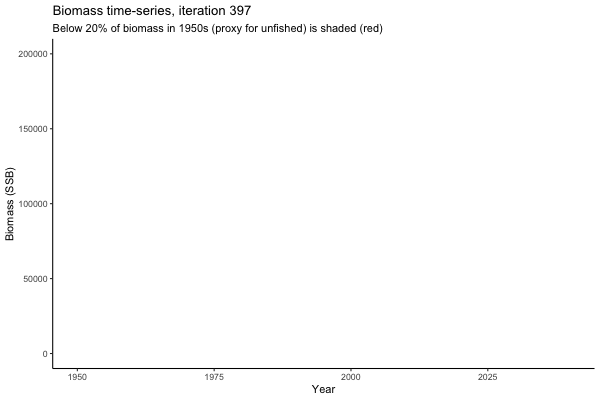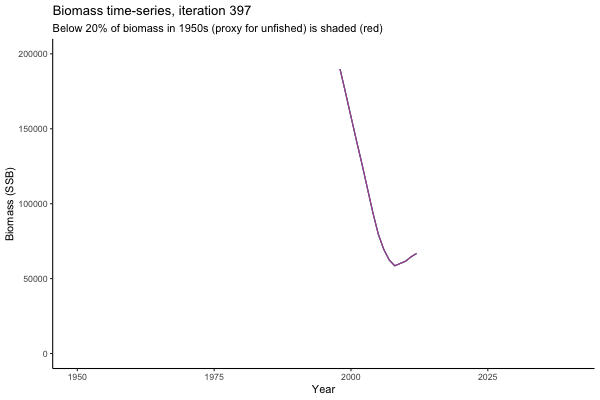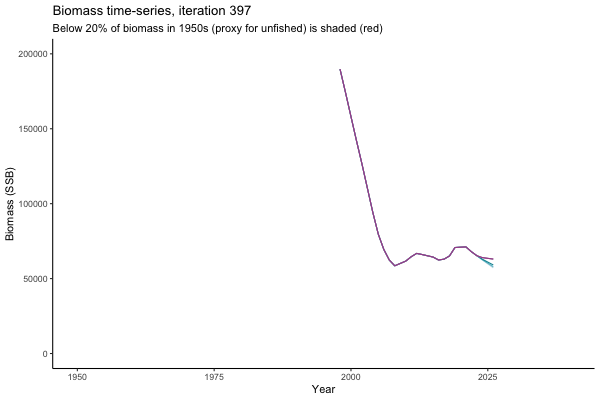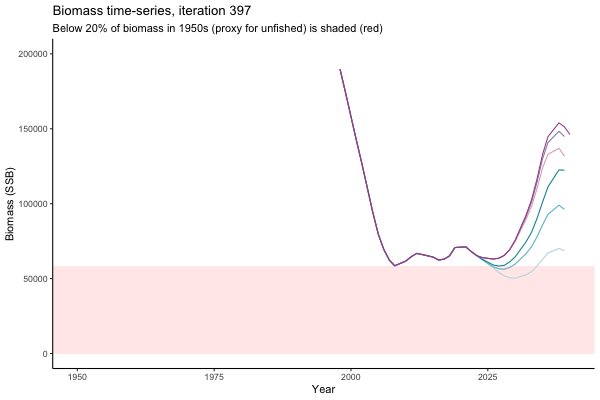
The first iteration we randomly picked assumes off-the-scale, higher than 200000t initial biomass (top right: Biomass time-series, iteration 497), and predicts rapid declines under the Hockey Stick HCRs (albeit still above 20% of average biomass in 1950s). In the second random set of simulations, all of the MPs are seen to lead relatively low biomass values (bottom right: Biomass time-series, iteration 14).
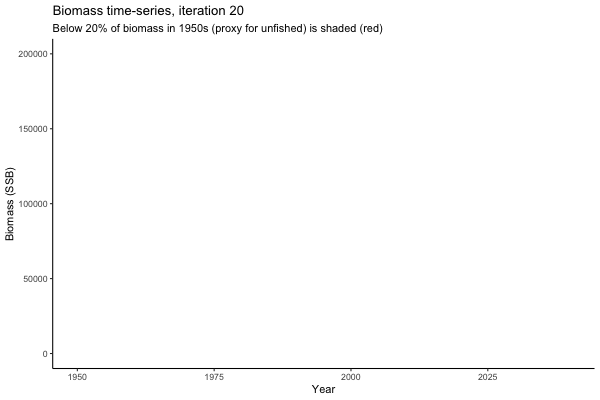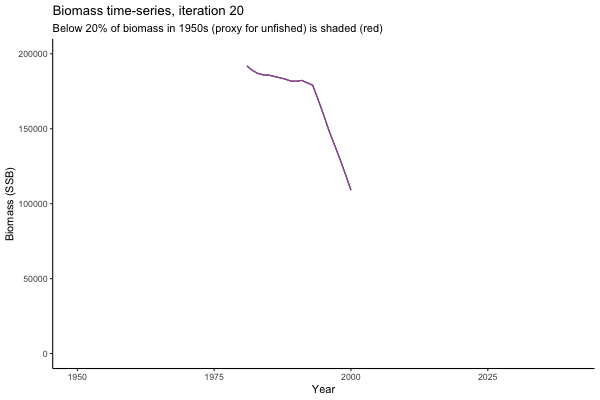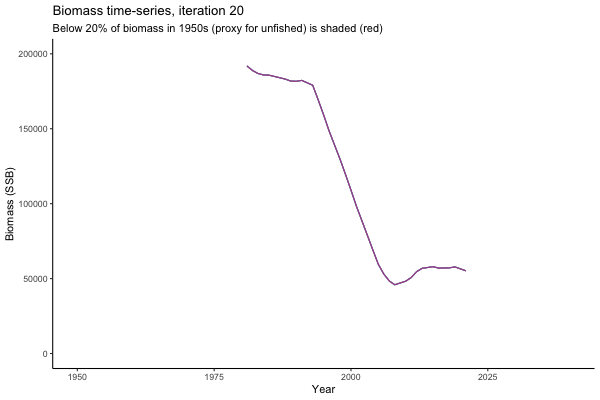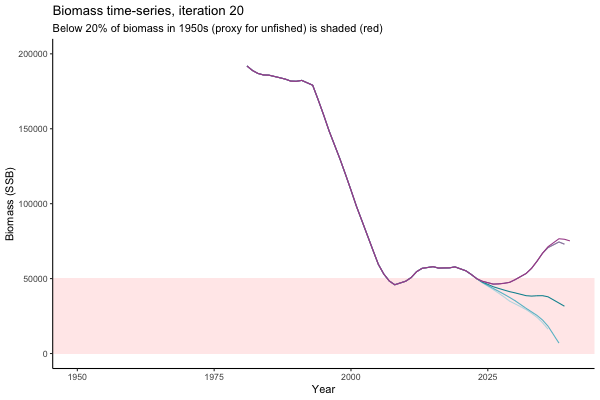
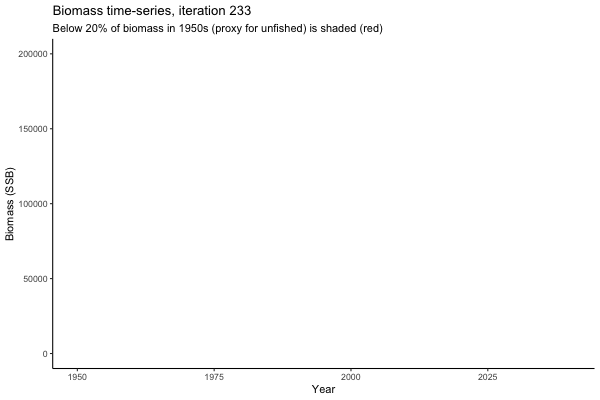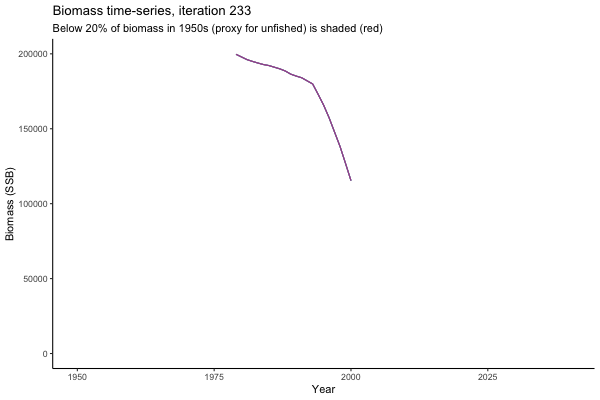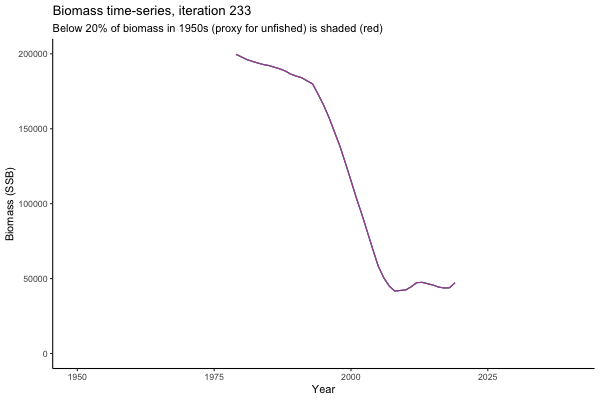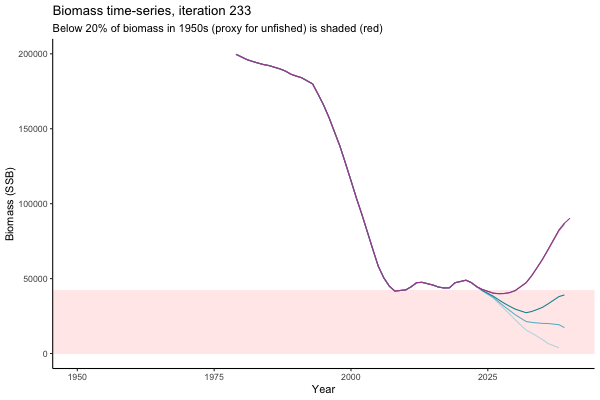
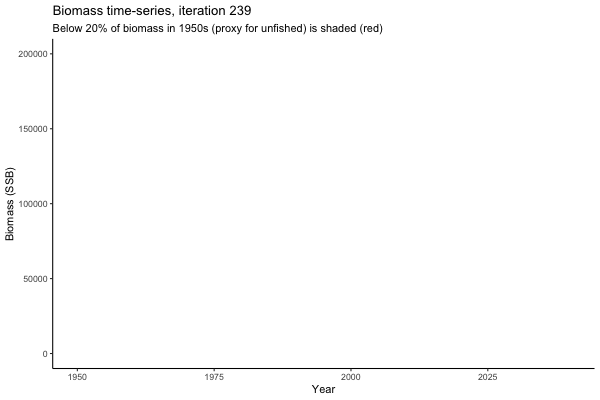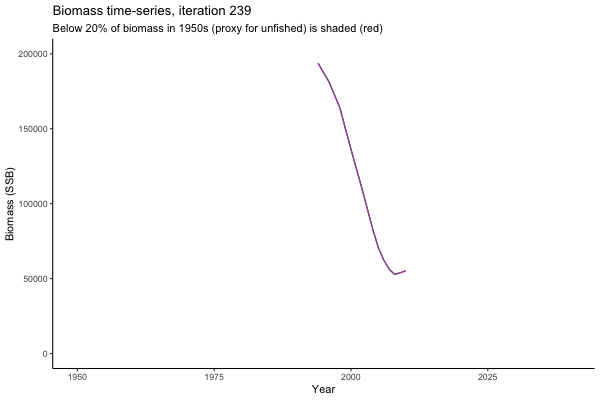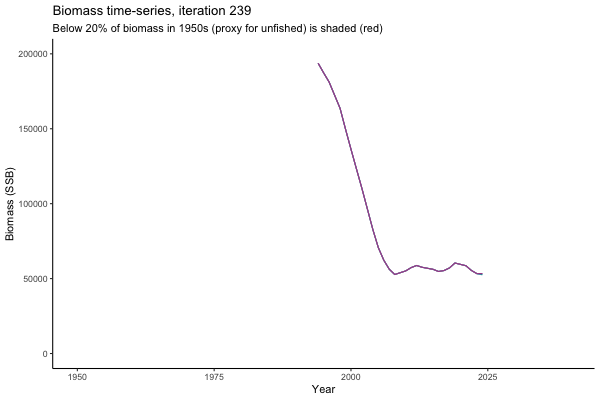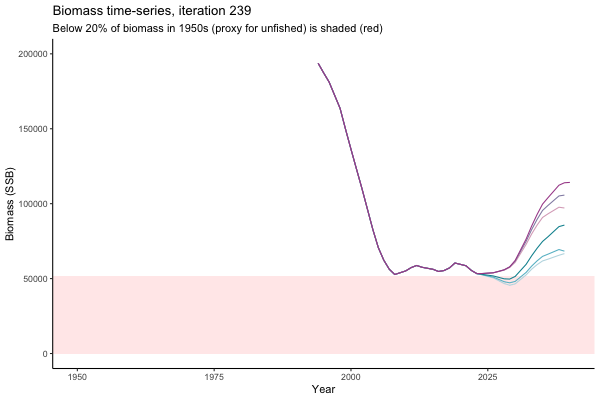
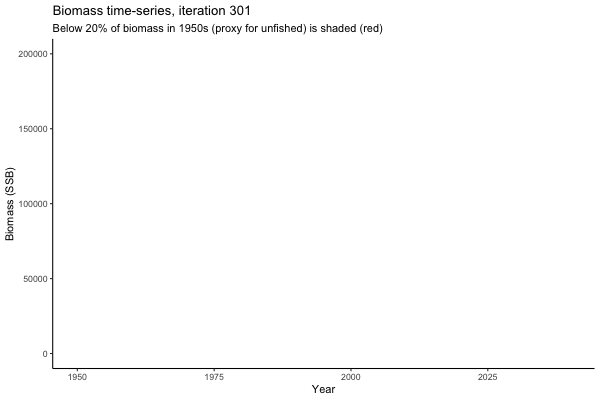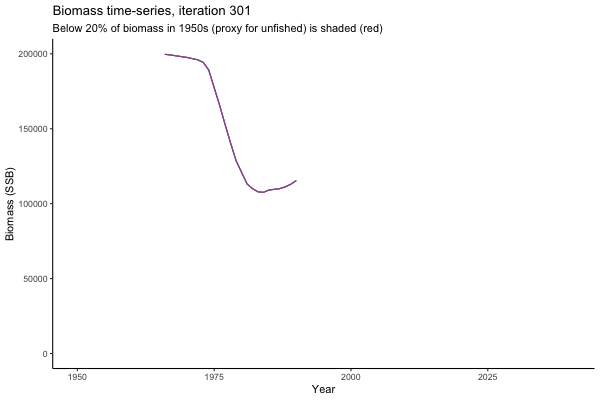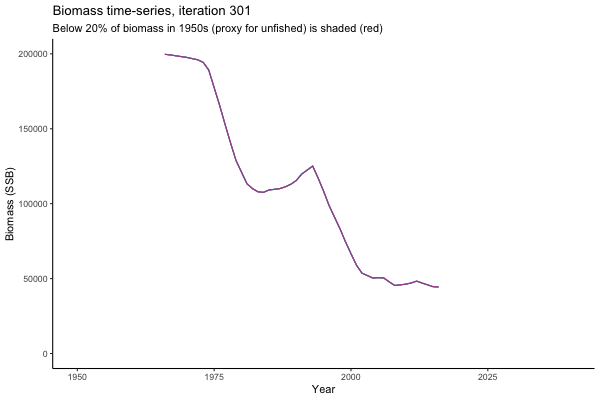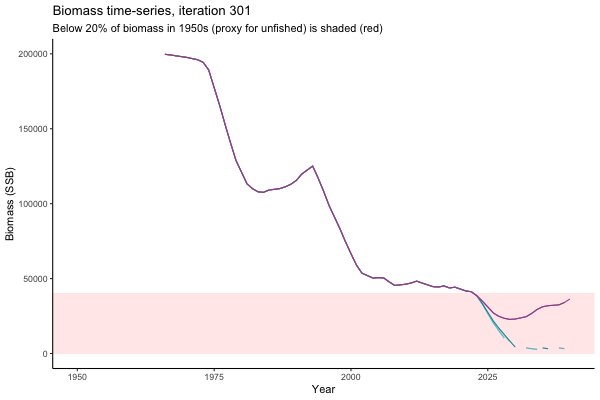
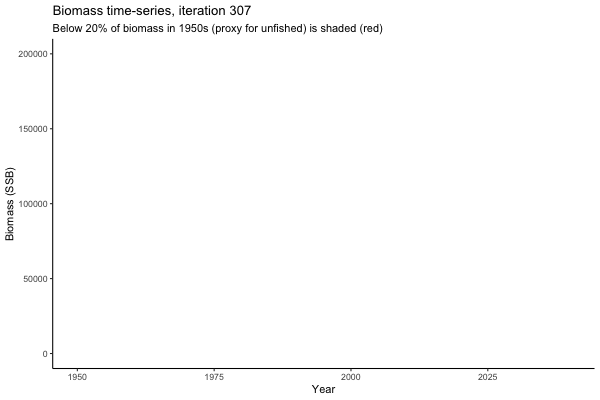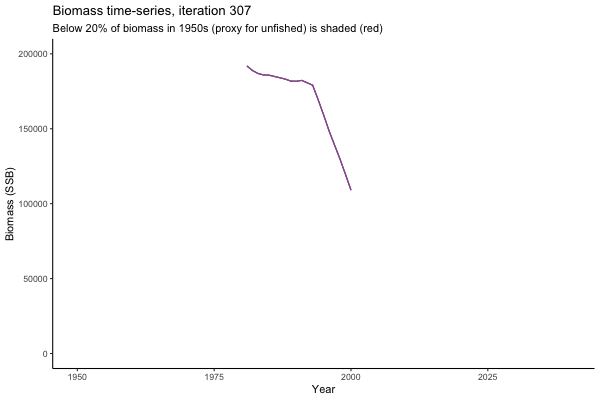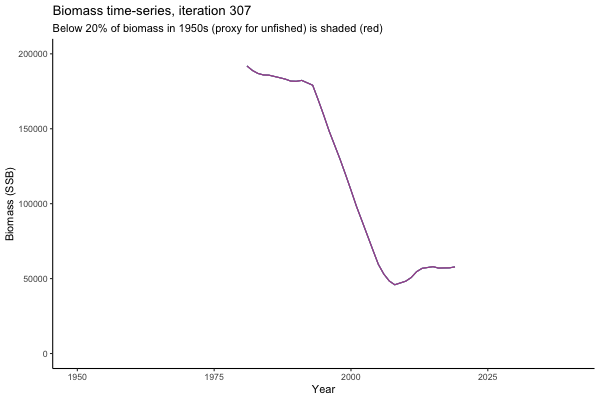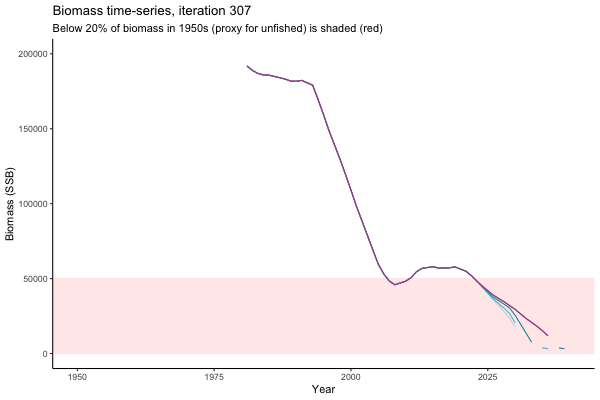
Different iterations represent alternative plausible levels of carrying capacity, hence the shaded region representing values below limit reference point or 20% of initial biomass (B0) is also different for each 'what if?' scenario.
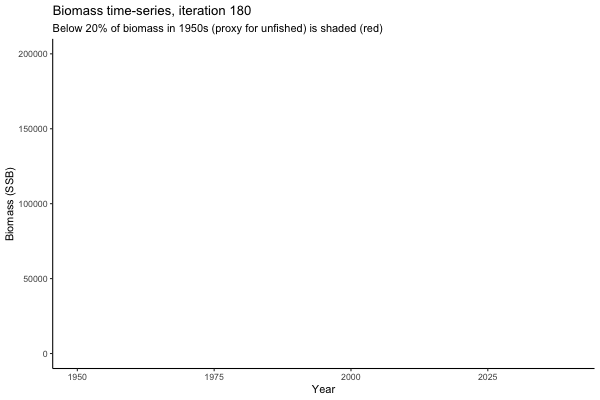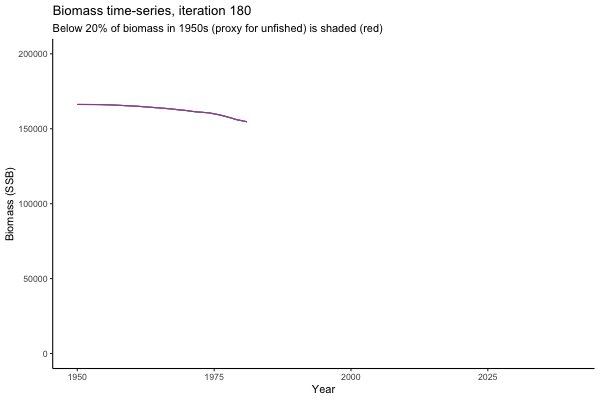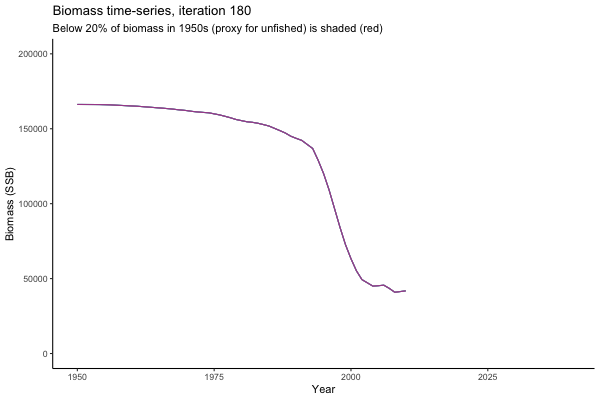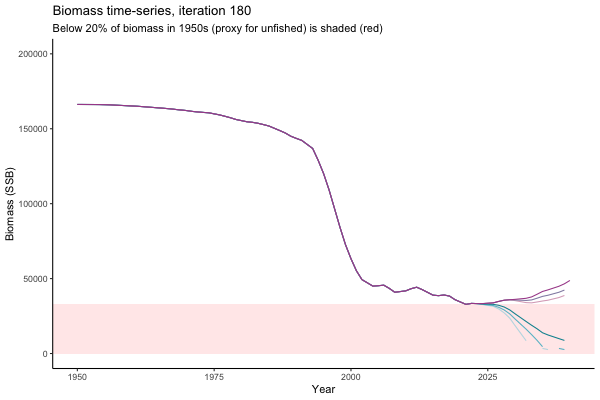
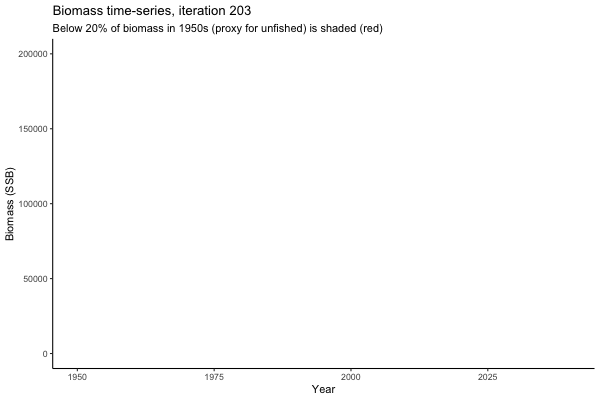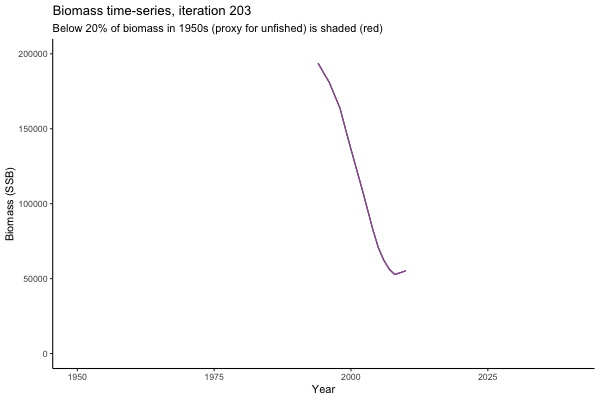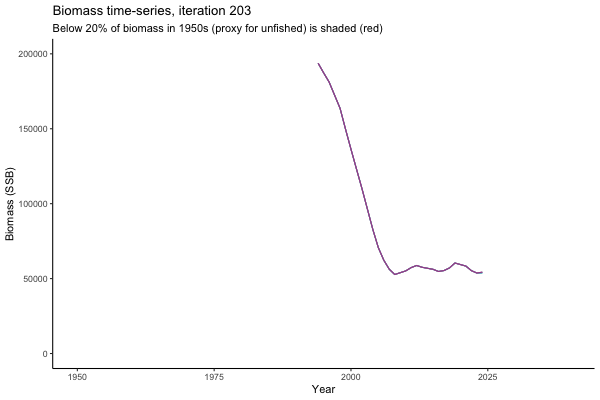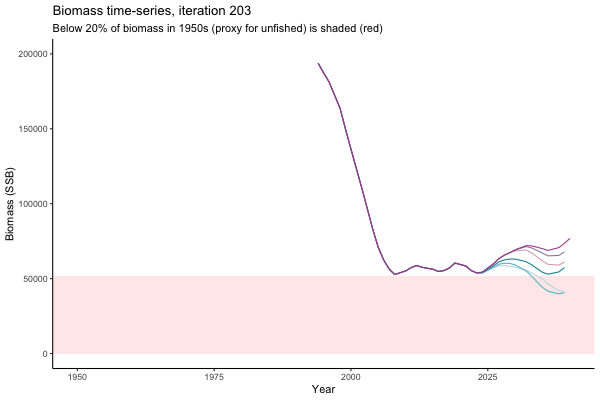
What if the stock is already depleted, which MP can be trusted to rebuild it? Here, you can browse those iterations in which the stock is below 80% BMSY in the mid-2020s, when management procedures kick in.
Please note: this section is still under construction.
It is common to use summary statistics to compare MPs rather than considering individual trajectories. However, skimming through this sub-set of trajectories it appears that Hockey Stick MPs, especially MP6, is significantly safer in a depleted fishery than the CPUE-based MPs. In fact, MP3 has only 11% chance of rebuilding the stock to above BMSY by 2039, compared to 49% chance for MP6. Moreover, MP1 ensures that the stock will end up below Blim (40% of BMSY) with 75% probability, by contrast such risk is only 4% with MP6.
This strong evidence in favour of MP6 (and against MP1) is masked in summary statistics when rebuilding scenarios are considered among all others. MP6 emerges as the only precautionary management procedure, however, it was tested under the assumption that it knows precisely how the stock is doing (at all times) and under the assumption of perfect implementation of management decisions. Further testing is required to select a management procedure fit for the real world.